Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
тюменский государственный архитектурно-строительный университет
Кафедра "Строительная механика"
Куриленко Е.Ю., Огороднова Ю.В.
Сопротивление материалов
сборник заданий
для выполнения расчетно-практической работы на тему:
«Расчеты на прочность и жесткость при центральном
растяжении-сжатии»
для студентов очной формы обучения всех специальностей, изучающих «Сопротивление материалов»
Тюмень – 2009 год
УДК
ББК
Куриленко Е.Ю., Огороднова Ю.В. Сопротивление материалов: сборник заданий для выполнения Расчетно-практической работы на тему: «Расчеты на прочность и жесткость при центральном растяжении-сжатии» для студентов очной формы обучения всех специальностей, изучающих сопротивление материалов. – Тюмень: РИЦ ГОУ ВПО ТюмГАСУ, 2009. – 74с.
Практикум разработан на основании рабочих программ ГОУ ВПО ТюмГАСУ дисциплины «Сопротивление материалов» для студентов очной формы обучения. Сборник содержит задачи для выполнения расчетно-практической работы на тему: «Расчеты на прочность и жесткость при центральном растяжении-сжатии».
Рецензент: Белова О.Ю.
Тираж 100 экз.
©ГОУ ВПО «Тюменский государственный архитектурно-строительный университет
©Куриленко Е.Ю., Огороднова Ю.В.
Содержание
Стр.
1. Статически определимые стержни………………..………………….4
2. Статически определимые стержневые системы....………………….17
3. Учет собственного веса …………..………………..………………….28
4. Статически неопределимые стержни и
стержневые системы…………………..……………..………………….41
5. Монтажные напряжения…………..………………..………………...56
Литература ……………………………………………………………….67
1. Статически определимые стержни
1.1. Подобрать (по сортаменту) номер двутавра, нагруженного как показано на рисунке, из условия прочности и определить величину абсолютной деформации стержня (рисунок 1.1., таблица 1.1.).
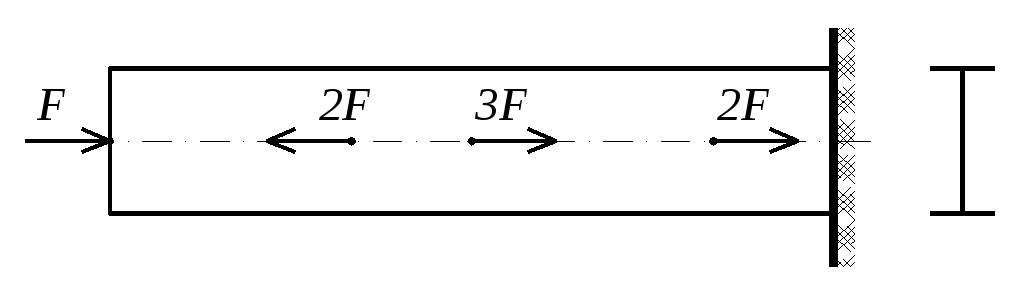
Рисунок 1.1.
Таблица 1.1.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
F, кН |
100 |
200 |
400 |
800 |
500 |
600 |
150 |
350 |
300 |
250 |
|
R, МПа |
210 |
220 |
230 |
240 |
235 |
225 |
215 |
220 |
240 |
235 |
1.2.
Стальная полоса шириной
и толщиной
ослаблена болтовым отверстием диаметром
,
расположенным на оси полосы. Определить
допустимое растягивающее полосу усилие,
если расчетное сопротивление материала
полосы на растяжение
,
а коэффициент запаса прочности равен
(Рисунок 1.2., таблица 1.2).
Рисунок 1.2.
Таблица 1.2.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d, мм |
20 |
50 |
75 |
80 |
100 |
40 |
60 |
50 |
75 |
10 |
|
h, мм |
10 |
8 |
12 |
16 |
20 |
14 |
12 |
10 |
20 |
8 |
|
b, см |
10 |
20 |
25 |
30 |
22 |
15 |
18 |
12 |
16 |
8 |
|
Rр, МПа |
240 |
200 |
210 |
220 |
200 |
210 |
220 |
240 |
200 |
210 |
|
n |
1,1 |
1,05 |
1,2 |
1,02 |
1,05 |
1,1 |
1,2 |
1,3 |
1,1 |
1,05 |
1.3.
Стальная полоса прямоугольного
поперечного сечения размером
,
нагруженная растягивающей силой
,
должна иметь коэффициент запаса прочности
не ниже
.
При каком наименьшем значении расчетного
сопротивления материала полосы будет
обеспечен заданный коэффициент запаса?
(Таблица 1.3.)
Таблица 1.3.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b, мм |
20 |
50 |
35 |
40 |
60 |
40 |
55 |
50 |
45 |
10 |
|
h, см |
10 |
20 |
25 |
30 |
22 |
15 |
18 |
12 |
16 |
8 |
|
F, тн |
40 |
200 |
175 |
250 |
300 |
110 |
175 |
105 |
135 |
50 |
|
n |
1,1 |
1,05 |
1,2 |
1,02 |
1,05 |
1,1 |
1,2 |
1,3 |
1,1 |
1,05 |
1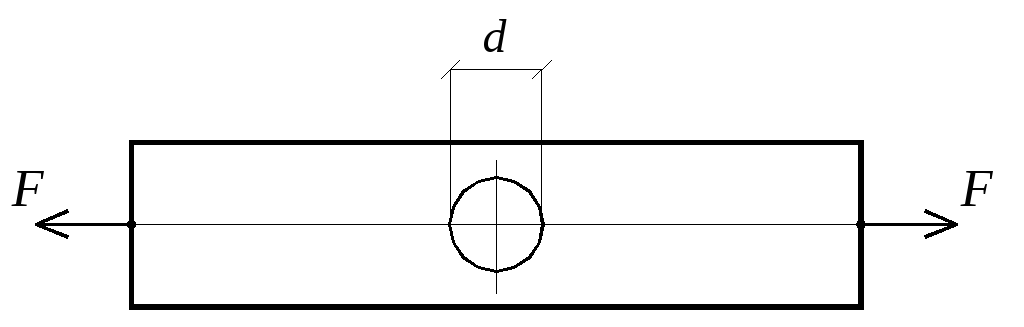
.4.
Стержень квадратного поперечного
сечения растягивается силами
.
Он ослаблен сквозным отверстием диаметром
.
Найти сторону сечения стержня из условия
прочности (рисунок 1.3., таблица 1.4.).
Рисунок 1.3.
Таблица 1.4.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
d, мм |
20 |
50 |
75 |
80 |
100 |
40 |
60 |
50 |
75 |
10 |
|
F, тн |
40 |
50 |
65 |
35 |
75 |
80 |
85 |
100 |
55 |
45 |
|
Rр, МПа |
180 |
200 |
210 |
220 |
130 |
150 |
180 |
200 |
160 |
180 |
1.5.
Под воздействием
приложенной нагрузки стержень укоротился
на величину
.
Определить величину нагрузки
.
Модуль упругости меди Ем=1,08105МПа,
модуль упругости
бронзы
Ебр=0,75105МПа.
(рисунок 1.4., таблица 1.5.)
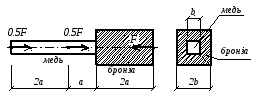
Рисунок 1.4.
Таблица 1.5.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b, мм |
20 |
50 |
75 |
80 |
100 |
40 |
60 |
50 |
75 |
10 |
|
a, м |
0,30 |
0,50 |
0,20 |
0,15 |
0,10 |
0,80 |
0,10 |
0,40 |
0,50 |
0,70 |
|
l, мм |
0,12 |
0,22 |
0,21 |
0,18 |
0,20 |
0,16 |
0,15 |
0,14 |
0,23 |
0,25 |
1.6. Стержень нагружен уравновешенной продольной нагрузкой в виде сосредоточенных и распределенных сил. По эпюре продольных сил определить значения и направления приложенной к стержню нагрузки (рисунок 1.5., таблица 1.6.).
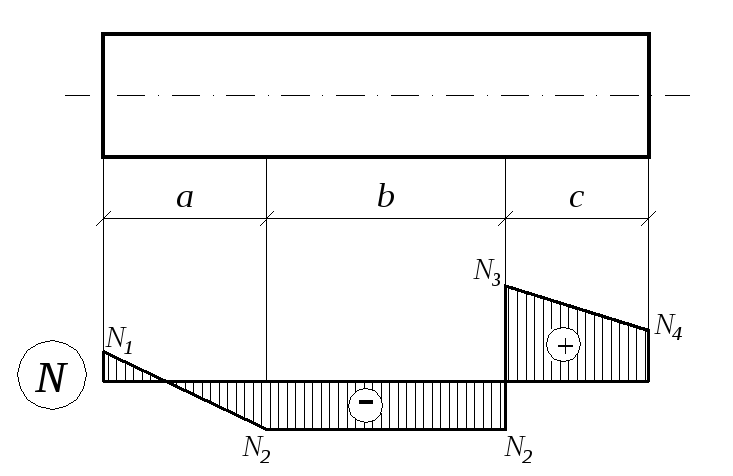
Рисунок 1.5.
Таблица 1.6.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
50 |
75 |
80 |
10 |
40 |
60 |
50 |
75 |
10 |
|
|
40 |
25 |
25 |
20 |
30 |
24 |
12 |
22 |
30 |
30 |
|
|
50 |
45 |
40 |
35 |
50 |
40 |
30 |
50 |
50 |
40 |
|
|
10 |
10 |
16 |
15 |
26 |
20 |
5 |
20 |
30 |
10 |
|
a, м |
3,0 |
5,0 |
2,0 |
2,5 |
1,0 |
0,8 |
1,2 |
2,4 |
3,5 |
4,0 |
|
b, м |
1,3 |
1,5 |
1,2 |
1,5 |
1,0 |
1,8 |
2,0 |
1,4 |
1,5 |
1,7 |
|
с, м |
4,0 |
3,5 |
2,4 |
2,0 |
0,8 |
1,0 |
2,5 |
2,0 |
5,0 |
3,0 |
,
кН
,
кН
,
кН
,
кН
1.7. Стальной стержень составлен из четырех равнобоких уголков и загружен сосредоточенными силами. Определить номер уголков из условия прочности (рисунок 1.6., таблица 1.7.).
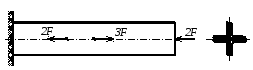
Рисунок 1.6.
Таблица 1.7.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
150 |
120 |
150 |
100 |
80 |
110 |
140 |
50 |
75 |
|
|
235 |
245 |
210 |
220 |
225 |
210 |
220 |
240 |
200 |
210 |
,
тн
,МПа
1.8.
Полый цилиндрический стержень длиной
под действием сжимающей силы укоротился
на величину
.
Наружный диаметр цилиндра
,
внутренний -
.
Определить величину сжимающей силы и
напряжения в стержне. Материал – медь
(таблица 1.8.).
Таблица 1.8.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
3,0 |
4,0 |
3,5 |
2,0 |
5,0 |
4,0 |
3,0 |
5,0 |
3,5 |
|
|
0,12 |
0,22 |
0,21 |
0,18 |
0,20 |
0,16 |
0,15 |
0,14 |
0,23 |
0,25 |
|
|
20 |
25 |
30 |
35 |
20 |
25 |
30 |
35 |
20 |
25 |
|
|
18 |
23 |
28 |
33 |
18 |
23 |
28 |
33 |
18 |
23 |
,
м
,
мм
,
см
,
см
1.9.
Чугунная труба длиной
нагружена сжимающей силой
.
Наружный диаметр трубы
,
толщина стенки
.
Определить относительное и абсолютное
укорочение трубы и проверить выполнение
условия прочности (таблица 1.9.).
Таблица 1.9.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,5 |
3,0 |
4,0 |
3,5 |
2,0 |
5,0 |
4,0 |
3,0 |
5,0 |
3,5 |
|
|
40 |
50 |
45 |
50 |
55 |
35 |
55 |
65 |
45 |
30 |
|
|
20 |
25 |
30 |
35 |
20 |
25 |
30 |
35 |
20 |
25 |
|
|
8 |
6 |
10 |
8 |
10 |
5 |
12 |
14 |
6 |
10 |
,
м
,
тн
,
см
,
мм
1.10. Проверить выполнение условия прочности для алюминиевой трубки, загруженной продольными силами, и определить ее относительное удлинение, если Еал=0,7105МПа, Rм=130МПа (рис. 1.7., таблица 1.10).
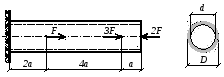
Рисунок 1.7.
Таблица 1.10.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
0,3 |
0,4 |
0,5 |
0,2 |
0,5 |
0,4 |
0,3 |
0,5 |
0,5 |
|
|
35 |
45 |
55 |
50 |
55 |
35 |
55 |
65 |
45 |
30 |
|
|
20 |
25 |
30 |
35 |
20 |
25 |
30 |
35 |
20 |
25 |
|
|
18 |
23 |
28 |
33 |
18 |
23 |
28 |
33 |
18 |
23 |
,
м
,
тн
,
см
,
см
1
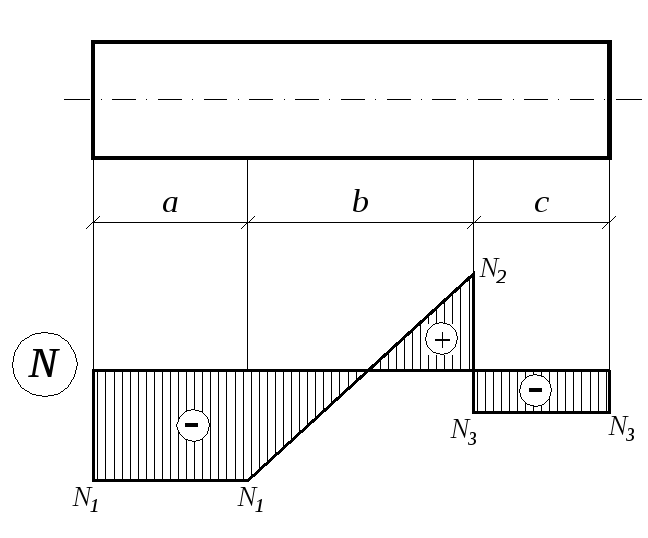.11.
Стержень нагружен уравновешенной
продольной нагрузкой в виде сосредоточенных
и распределенных сил. По эпюре продольных
сил определить значения и направления
приложенной к стержню нагрузки (рисунок
1.8., таблица 1.11).
Рисунок 1.8.
Таблица 1.11.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
50 |
75 |
80 |
10 |
40 |
60 |
50 |
75 |
10 |
|
|
40 |
25 |
25 |
35 |
30 |
24 |
12 |
22 |
30 |
30 |
|
|
20 |
45 |
40 |
20 |
50 |
40 |
30 |
50 |
50 |
40 |
|
a, м |
1,3 |
2,0 |
2,0 |
2,5 |
1,0 |
1,8 |
1,2 |
1,4 |
1,5 |
1,5 |
|
b, м |
3,0 |
1,5 |
2,0 |
1,5 |
1,0 |
0,8 |
2,0 |
2,4 |
3,5 |
4,0 |
|
с, м |
4,0 |
3,5 |
2,4 |
2,0 |
0,8 |
1,0 |
2,5 |
2,0 |
5,0 |
3,0 |
,
кН
,
кН
,
кН
1.12.
Клеть шахтного подъемника подвешена к
тросу с площадью поперечного сечения
,
длина которого при нагружении его только
весом клети равна
.
При загрузке клети рудой весом
удлинение троса оказалось равным
.
Определить модуль упругости троса
(таблица 1.12.).
Таблица 1.12.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
130 |
140 |
135 |
120 |
150 |
140 |
130 |
150 |
135 |
|
|
1,1 |
1,3 |
1,7 |
1,6 |
1,8 |
0,8 |
0,2 |
0,8 |
0,6 |
1,4 |
|
|
12,0 |
12,5 |
13,0 |
13,5 |
14,0 |
14,5 |
15,0 |
10,0 |
10,5 |
11,0 |
|
|
20 |
25 |
30 |
35 |
40 |
15 |
5 |
12 |
8 |
22 |
,
м
,
мм
,
см2
,
тн
1.13.
Полиэтиленовая трубка кольцевого
поперечного сечения с наружным диаметром
растянута силой
.
Определить необходимую толщину стенки,
если расчетное сопротивление на
растяжение
(таблица 1.13.).
Таблица 1.13.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,0 |
15,0 |
12,0 |
9,0 |
10,0 |
8,0 |
11,0 |
14,0 |
5,0 |
7,5 |
|
|
10,0 |
15,0 |
13,0 |
11,0 |
12,0 |
12,5 |
11,5 |
9,0 |
7,5 |
9,5 |
,
кН
,
см
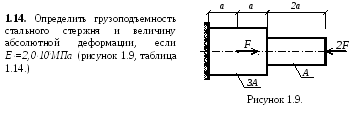
Таблица 1.14.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,0 |
12,5 |
13,0 |
13,5 |
14,0 |
14,5 |
15,0 |
10,0 |
10,5 |
11,0 |
|
|
1,5 |
1,3 |
1,4 |
1,5 |
1,2 |
1,5 |
1,4 |
1,3 |
1,5 |
1,2 |
|
|
210 |
215 |
220 |
210 |
225 |
220 |
210 |
230 |
225 |
235 |
,
см2
,
м
,МПа
1.15. Определить грузоподъемность деревянного стержня и определить его абсолютное укорочение, если Е=0,1105МПа (рисунок 1.10, таблица 1.15).
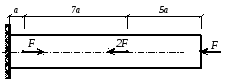
Рисунок 1.10.
Таблица 1.15.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
350 |
300 |
320 |
400 |
250 |
350 |
330 |
300 |
400 |
300 |
|
|
0,5 |
0,3 |
0,4 |
0,5 |
0,2 |
0,5 |
0,4 |
0,3 |
0,5 |
0,2 |
|
|
40 |
41 |
38 |
42 |
43 |
44 |
45 |
46 |
42 |
40 |
,
см2
,
м
,МПа
Таблица 1.16.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30,0 |
45,0 |
35,0 |
25,0 |
20,0 |
50,0 |
65,0 |
60,0 |
55,0 |
40,0 |
|
|
180 |
190 |
200 |
185 |
180 |
210 |
200 |
195 |
180 |
180 |
,
тн
,
МПа
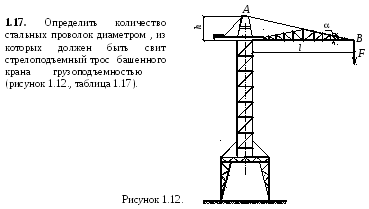
Таблица 1.17.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,5 |
13,0 |
14,0 |
13,5 |
12,0 |
15,0 |
14,0 |
13,0 |
15,0 |
13,5 |
|
|
2,2 |
3,2 |
2,1 |
2,8 |
2,0 |
2,6 |
2,5 |
2,4 |
3,3 |
3,5 |
|
|
10,0 |
12,0 |
8,0 |
7,5 |
11,0 |
9,5 |
10,0 |
10,5 |
12,5 |
8,5 |
|
|
5,0 |
6,0 |
3,0 |
6,0 |
4,0 |
3,0 |
4,0 |
5,0 |
6,0 |
4,0 |
,
м
,
м
,
тн
,
мм
1.18.
Трос растянут усилием
.
Он состоит из проволок диаметром
.
Определить число проволок в тросе из
условия прочности (таблица 1.18.).
Таблица 1.18.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,0 |
6,0 |
3,0 |
6,0 |
4,0 |
3,0 |
4,0 |
5,0 |
6,0 |
4,0 |
|
|
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
2,5 |
3,5 |
3,2 |
2,8 |
3,3 |
|
|
130 |
180 |
220 |
210 |
225 |
160 |
170 |
200 |
220 |
180 |
,
мм
,
тн
,
МПа
1.19.
Две проволоки, одна стальная, другая
медная, имеют одинаковую длину и нагружены
одинаковыми осевыми растягивающими
усилиями. Медная проволока имеет диаметр
.
Чему равен диаметр стальной проволоки,
если обе проволоки удлиняются на
одинаковую величину? (таблица 1.19)
Таблица 1.19.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,0 |
4,0 |
5,0 |
6,0 |
3,0 |
4,0 |
5,0 |
6,0 |
3,0 |
4,0 |
|
|
2,2 |
2,1 |
2,0 |
1,9 |
2,2 |
2,1 |
2,0 |
2,2 |
1,9 |
2,1 |
|
|
1,1 |
1,2 |
1,3 |
1,0 |
1,1 |
1,2 |
1,3 |
1,1 |
1,2 |
1,3 |
,
мм
,
МПа
,
МПа
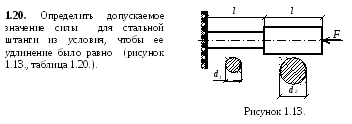
Таблица 1.20.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
12 |
16 |
9 |
15 |
12 |
10 |
14 |
7 |
12 |
|
|
16 |
20 |
22 |
20 |
25 |
24 |
18 |
20 |
16 |
22 |
|
|
2,2 |
2,1 |
2,0 |
1,9 |
2,2 |
2,1 |
2,0 |
2,2 |
1,9 |
2,1 |
|
|
0,12 |
0,13 |
0,15 |
0,20 |
0,25 |
0,22 |
0,16 |
0,21 |
0,11 |
0,26 |
|
|
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,6 |
0,2 |
0,4 |
0,6 |
0,3 |
,
мм
,
мм
,
МПа
,
мм
,
м
Таблица 1.21.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,0 |
15,0 |
18,0 |
20,0 |
24,0 |
15,0 |
18,0 |
16,0 |
20,0 |
22,0 |
|
|
40 |
35 |
50 |
45 |
60 |
30 |
40 |
35 |
60 |
65 |
|
|
220 |
215 |
210 |
220 |
225 |
220 |
210 |
230 |
225 |
235 |
,
тн
,
мм
,
МПа
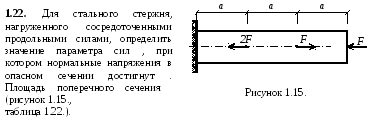
Таблица 1.22.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12,0 |
12,5 |
13,0 |
13,5 |
14,0 |
14,5 |
15,0 |
10,0 |
10,5 |
11,0 |
|
|
0,5 |
0,3 |
0,4 |
0,5 |
0,2 |
0,5 |
0,4 |
0,3 |
0,5 |
0,2 |
|
|
220 |
215 |
210 |
220 |
225 |
220 |
210 |
230 |
225 |
235 |
,
см2
,
м
,
МПа
1.23.
В поперечном сечении стержня фермы
растягивающее усилие равно
.
Проверить прочность стержня, если он
состоит из двух равнобоких уголков
(таблица 1.23.).
Таблица 1.23.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
35 |
40 |
35 |
30 |
30 |
35 |
55 |
60 |
65 |
|
Уголок |
75*5 |
75*6 |
75*7 |
80*6 |
80*7 |
80*8 |
90*8 |
90*9 |
100*8 |
100*7 |
|
|
220 |
215 |
210 |
220 |
225 |
220 |
210 |
230 |
225 |
235 |
,
тн
,МПа
1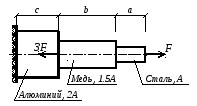
.24.
Стержень нагружен продольными силами.
После приложения нагрузки его полная
длина уменьшится на величину
.
Определить значение параметра сил
,
если
,
,
(рисунок 1.16., таблица 1.24.).
Рисунок 1.16.
Таблица 1.24.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,0 |
8,5 |
9,0 |
9,5 |
10,0 |
10,5 |
11,0 |
11,5 |
12,0 |
12,5 |
|
a, м |
0,3 |
0,2 |
0,1 |
0,4 |
0,1 |
0,2 |
0,3 |
0,4 |
0,2 |
0,3 |
|
b, м |
0,15 |
0,22 |
0,25 |
0,18 |
0,20 |
0,26 |
0,16 |
0,15 |
0,20 |
0,12 |
|
с, м |
0,2 |
0,3 |
0,1 |
0,2 |
0,3 |
0,1 |
0,2 |
0,3 |
0,1 |
0,2 |
|
|
1,2 |
1,3 |
1,5 |
2,0 |
2,5 |
2,2 |
1,6 |
2,1 |
1,1 |
2,6 |
,
см2
,
мм
1.25.
Определить напряжения и деформации в
стальном тросе
длиной
и площадью поперечного сечения
,
если максимальный вес грунта, извлекаемого
из опускного колодца краном, не превышает
(рисунок 1.17., таблица 1.25.).
Рисунок
1.17.
Таблица 1.25.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8,5 |
9,0 |
9,5 |
10,0 |
12,0 |
8,0 |
9,0 |
11,0 |
8,5 |
9,5 |
|
|
10,0 |
12,0 |
8,0 |
7,5 |
11,0 |
9,5 |
10,0 |
10,5 |
12,5 |
8,5 |
|
|
12,0 |
14,0 |
9,5 |
12,5 |
10,0 |
11,5 |
13,0 |
14,0 |
9,0 |
13,5 |
,
м
,
тн
,
см2
1.26.
Полное удлинение стержня квадратного
поперечного сечения равно
.
Исходя из этого условия определить
размер сечения стержня и построить
эпюру напряжений (рисунок 1.18., таблица
1.26.).
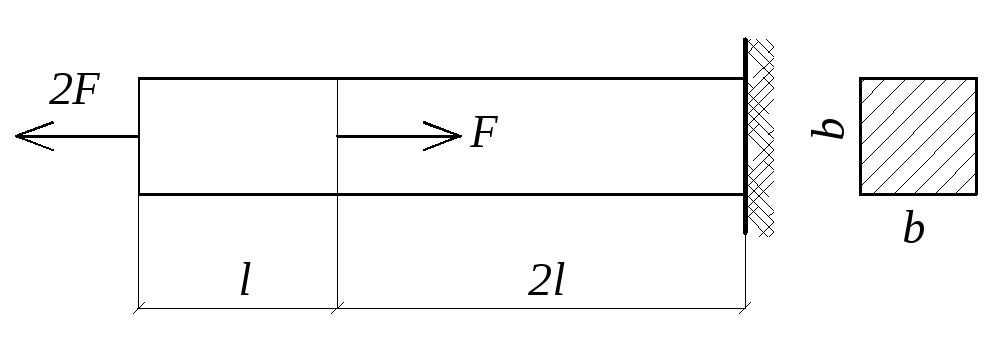
Рисунок 1.18.
Таблица 1.26.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,01 |
0,02 |
0,03 |
0,01 |
0,02 |
0,03 |
0,01 |
0,02 |
0,03 |
0,01 |
|
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
|
|
50 |
60 |
70 |
80 |
90 |
100 |
110 |
90 |
80 |
70 |
,
мм
,
м
,
кН
1.27.
Стальной стержень круглого сечения
растягивается усилием
.
Относительное удлинение стержня не
должно превышать
,
а напряжение не должно быть больше
.
Найти наименьший диаметр стержня,
удовлетворяющий этим условиям, если
(таблица
1.27.).
Таблица 1.27.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
60 |
70 |
80 |
90 |
100 |
110 |
90 |
80 |
70 |
|
|
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
1,0 |
1,5 |
2,0 |
|
|
220 |
215 |
210 |
220 |
225 |
220 |
210 |
230 |
225 |
235 |
,
кН
,МПа
1.28.
При подвешивании некоторого груза к
стальной проволоке длиной
и диаметром
,
ее удлинение оказалось равным
.
Затем тот же груз был подвешен к медной
проволоке длиной
с диаметром
,
и в этом случае удлинение получилось
равным
.
Зная модуль упругости стальной проволоки
(
),
определить модуль упругости медной
(таблица 1.28.).
Таблица 1.28.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,0 |
2,1 |
2,2 |
2,3 |
2,4 |
2,5 |
2,6 |
2,7 |
2,8 |
3,0 |
|
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
,
см
,
м
1.29. Стальной стержень имеет в правой части сплошное, а в левой части кольцевое сечение. Определить напряжения в обеих частях стержня и полное его удлинение (рисунок 1.19., таблица 1.29.).
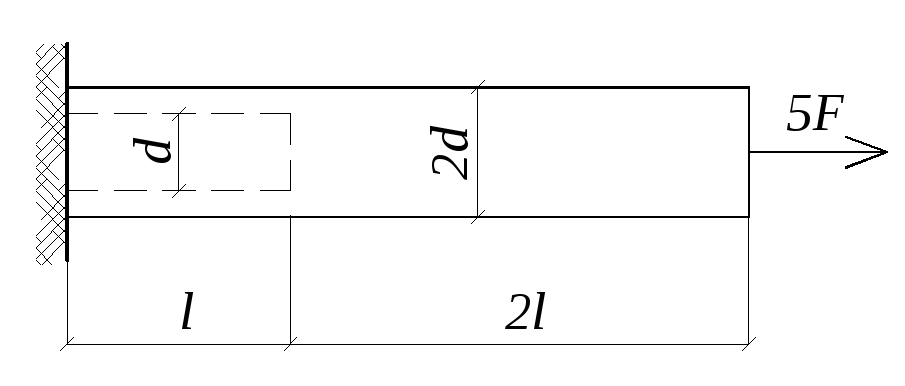
Рисунок 1.19.
Таблица 1.29.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
|
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
|
|
50 |
60 |
70 |
80 |
90 |
100 |
110 |
90 |
80 |
70 |
,
мм
,
м
,
кН
1.30.
Для медного стержня с прямоугольным
поперечным сечением, нагруженного
продольными силами, определить наибольшее
нормальное напряжение, полное удлинение
размеров поперечного сечения: высоты
в сечении
,
ширины
в сечении
,
если
(рисунок
1.20., таблица 1.30.).
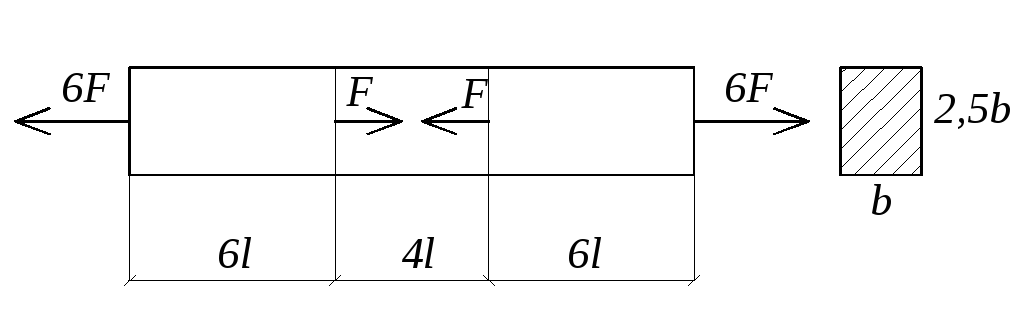
Рисунок 1.20.
Таблица 1.30.
|
Исх. данные |
Номер группы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
1,1 |
1,2 |
1,3 |
1,4 |
|
|
50 |
60 |
70 |
80 |
90 |
55 |
65 |
75 |
85 |
95 |
|
|
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
2,5 |
3,5 |
4,5 |
5,5 |
6,5 |
,
м
,
кН
,
см