12. Двухфакторный дисперсионный анализ без повторений и с повторениями

1. Краткие сведения из теории статистики

Продолжая тему главы 11, в которой была рассмотрена проце­дура однофакторного дисперсионного анализа, перейдем к задаче о действии на результативный признак Y двух факторов – А и В. Такие задачи характерны как для промышленных и технологичес­ких экспериментов, так и для гуманитарных исследований. Ти­пичный пример — выяснение зависимости качества пряжи от ти­па станка и вида сырья, из которой она изготавливается (см. при­мер 1).

Логика однофакторного и двухфакторного дисперсионного анализа во многом схожа и состоит в следующем.

Пусть - математическое ожидание результативного призна­ка Y при уровне - математическое ожидание результативного признака Y при уровне 2. Если при изменении уровня фактора A групповые математические ожидания не изменяются, т.е. , то считаем, что результативный признак не зависит от фактора A, в противном случае такая зависимость имеется. Аналогично, если при измене­нии уровня фактора В сохраняется равенство , то считаем, что У не зависит от фактора В. Но поскольку числовые значения математических ожиданий неизвестны, возникает зада­ча проверки следующих гипотез:

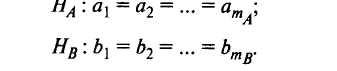
Проверять эти гипотезы, так же как и в задаче однофакторного дисперсионного анализа, можно только при соблюдении сле­дующих требований:

1. при различных сочетаниях уровней факторов А и В наблю­дения независимы;

2. при каждом сочетании уровней факторов А и В результатичный признак Y имеет нормальный закон распределения с постоянной для различных сочетаний генеральной дисперсией .

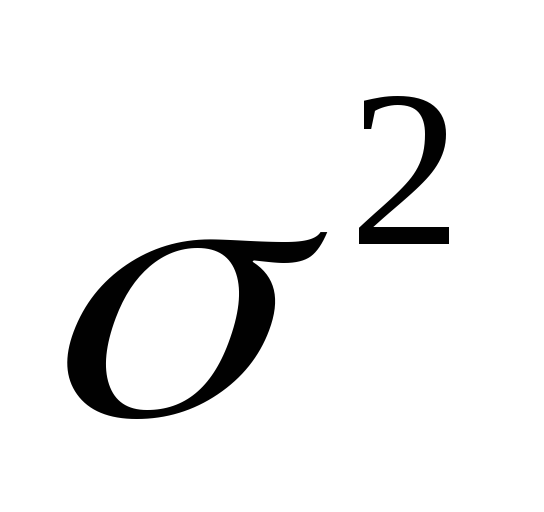Основой проведения двухфакторного дисперсионного анализа служит комбинационная группировка по двум факторам с последующим разложением дисперсии результативного признака по формуле

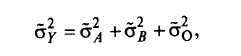
где - общая выборочная дисперсия — показатель вариации наблюдаемых «игреков», вызванной влиянием на Y фактора А фактора В и остаточных факторов;

- дисперсия групповых средних по фактору А — показатель вариации наблюдаемых «игреков», вызванной влиянием на Y фактора А;

- дисперсия групповых средних по фактору В — показатель вариации наблюдаемых «игреков», вызванной влиянием на У фактора В;

- средняя групповых дисперсий — показатель вариации наблюдаемых «игреков», вызванной влиянием на Y остаточных факторов.

На основе данного разложения для генеральной дисперсии находятся четыре несмещенные оценки: . Приччем оценка является несмещенной оценкой в любом случае, оценка - при выполнении гипотезы , оценка - при выполнении гипотезы , а оценка — при выполнении гипотез Н_А и Н_B.

Проверка гипотезы основывается на сравнении дисперсий . В математической статистике доказывается, что если гипотеза Н_А верна, то величина

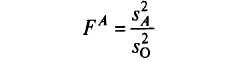
имеет F-распределение с числом степеней свободы , т.е.

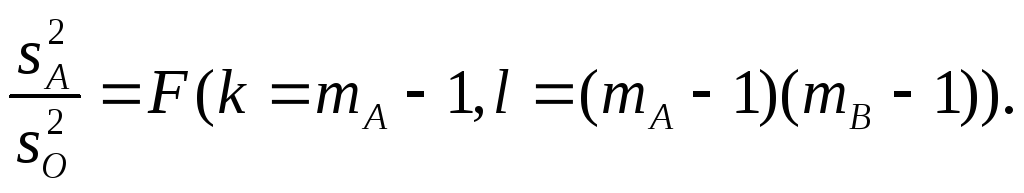
Аналогичным образом рассчитывается и величина F^B.

Проверка выдвинутых гипотез осуществляется так же, как и при однофакторном дисперсионном анализе, и состоит в нахожде­нии правосторонних критических интервалов с последующим контролем попадания (или непопадания) в данный интервал расчетных значений (или ). Если расчетное значение попадает в критический интервал, то гипотеза Н_А (Н_в) отвергается, т.е. считается, что фактор А (В) влияет на результативный признак У.

Двухфакторный дисперсионный анализ может иметь две разновидности: без повторений и с повторениями. В первом случае каждому уровню факторов соответствует только одна выборка данных, во втором - определенным уровням факторов может соответствовать более одной выборки данных.