3. Нечеткие кванторы
Как
известно, логика предикатов отличается
от логики высказываний тем, что в первой
имеются операции (кванторы), относящиеся
к предикату как к целому. Так, квантор
эквивалентен высказыванию: «все
обладают свойством
».
В «чёткой» логике это высказывание
может быть только истинным или только
ложным. В нечёткой логике допускаются
и промежуточные значения истинности.
Воспользуемся
известным определением квантора
в виде конъюнкции всех
,
когда
пробегает всё множество
:
.
При переходе к векторному представлению используем конъюнктивную матрицу (2)
.
Легко
убедиться, что 1-компонента (истинностная
компонента) высказывания
равна произведению
.
Получившееся выражение обобщает соответствующую формулу «чёткой» логики и сводит её к простому (нелогическому) алгебраическому выражению.
Аналогичным
образом вычисляем 1-компоненту высказывания
,
включающего нечёткий квантор существования
.
В
предельном случае чёткой логики это
выражение обращается в единицу, если
хотя бы одна из компонент
обращается в нуль. В нечёткой логике
величина
может иметь значения меньшие единицы.
Кроме
кванторов
в нечеткой логике важную роль играет
операция устранения нечеткости –
«дефазификация». Эта операция применяется
в тех случаях, когда множество
,
на котором задан предикат, является
числовым. Наиболее употребительны
следующие формулы:
.
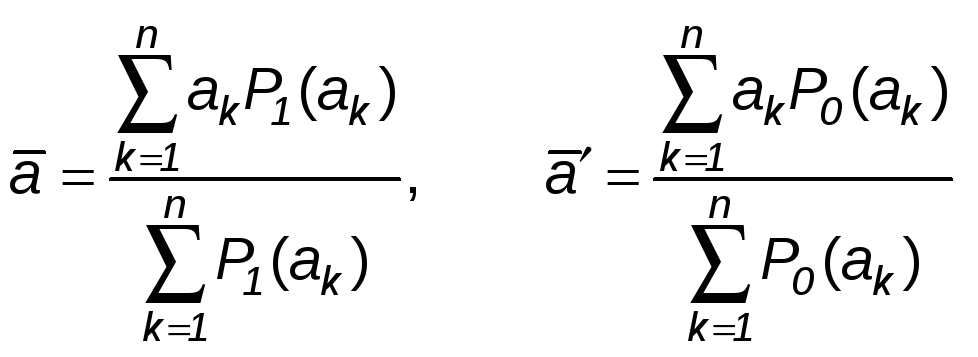(13)
4. Пример нечёткого вывода
Нечёткая
логика находит многочисленные приложения
для описания поведения интеллектуальных
систем. Мы рассмотрим иллюстративный
пример нечёткого вывода в задаче о
назначения оплаты за качество работы.
Будем считать, что качество работы
оценивается в баллах по десятибалльной
шкале и описывается нечётким предикатом
,
.
Уровень оплаты задается нечётким
предикатом
.
в процентах от максимальной ставки.
Правило назначения оплаты описывается
предикатом
,
который определяет сложную связь между
качеством работы и уровнем оплаты в
соответствии с логической формулой
(9).
|
|
|
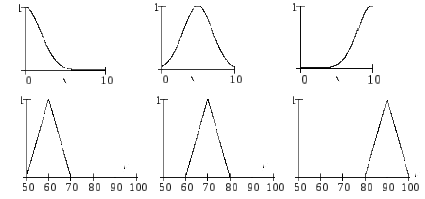
Рис. 2.
Входные значения истинностных компонент
предикатов
|
,
где
Введем
перекрывающиеся эмпирически заданные
нечёткие предикаты качества работы
(«плохо», «хорошо», «отлично») и
соответствующие предикаты уровня оплаты
,
представленные на рис. 2. Предполагая,
что в каждом случае справедливы
соотношения (10), находим «частные»
правила
,
,
откуда по формулам (11) выводим общее
правило, задаваемое предикатом
,
и посылку
.
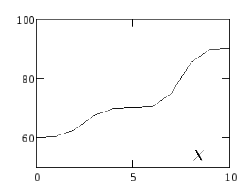
Теперь по правилу (9) выводим уровень
оплаты в зависимости от качества работы,
используя описанный выше метод устранения
нечеткости. Результат представлен на
графике рис. 3.
|
|
Рис. 3.
Результат расчета оплаты
|
(в
процентах от максимального значения)
в зависимости от качества труда
.
Расчет проведен на основании входных
данных, показанных на рис. 2. Величина
найдена
дефазификацией
по формуле (13)5. Заключение
В
стандартном изложении нечёткой логики
используется понятие лингвистической
переменной (ЛП)
(см., например, [7, 8]). Как и предикат ЛП
определяется на некотором множестве
,
но имеет областью значений «степень
принадлежности»
точек множества
данной ЛП. В зависимости от контекста
степень принадлежности трактуется либо
как истинностное значение нечёткой
логической переменной, либо как нечёткие
значения характеристической функции.
Нечёткие логические переменные трактуются
как «одномерные», логические правила
и вводятся как некоторые эмпирические
законы. Таким же образом вводятся и
операции над нечёткими множествами.
Рассмотренная выше схема применения
нечётких предикатов в векторно-матричном
представлении позволяет ввести логические
операции без произвольных допущений.
Логические операции над нечёткими
переменными описываются теми же самыми
тензорами, что и в «чёткой» логике. В
результате получается гибкая и
обоснованная система расчетов, содержащая
эмпирические экспертные оценки только
«на входе» алгоритмов.
Литература
1. Марценюк М.А. Матричное представление нечеткой логики / Труды IX международной конференции "Интеллектуальные системы и компьютерные науки", Москва, МГУ, 2006. Т. 4. С. 32-36.
2. Марценюк М.А. Матричное представление нечеткой логики / Нечеткие системы и мягкие вычисления. Том 2, № 3, 2007. С. 7-36.
3. Mizraji E. Vector logics: The matrix-vector representation of logical calculus / Fuzzy Sets and Systems. V. 50, 1992. P. 179-185.
4. Mizraji E. Modalities in Vector Logic. / Notre Dame Journal of Formal Logic. V. 35, N. 2, 1994. P. 272- 283.
5. Девятков В.В. Системы искусственного интеллекта. М.: Из-во МГТУ им. Н.Э.Баумана, 2001. – 352 с.
6. Рассел С., Норвиг П. Искусственный интеллект: современный подход. 2-е издание. М.: Изд. дом Вильямс, 2006. – 1408 с.
7. Рыжов А.П. Элементы теории нечётких множеств и её приложений. М.: МГУ, 2003. – 180 с.
8. Круглов В.В., Дли М.И. Интеллектуальные информационные системы. Компьютерная поддержка систем нечёткой логики и нечёткого вывода. М.: ИФМЛ, 2002. – 256 с.