5. Расчет координат ири

Современные комплексы местоопределения ИРИ строятся на основе использования следующих способов определения местоположения ИРИ: угломерного, угломерно-дальномерного, разностно-дальномерного (гиперболического), дальномерного и др. Наибольшее распространение в настоящее время получили угломерный и дальномерный способы местоопределения ИРИ.

Угломерный способ.

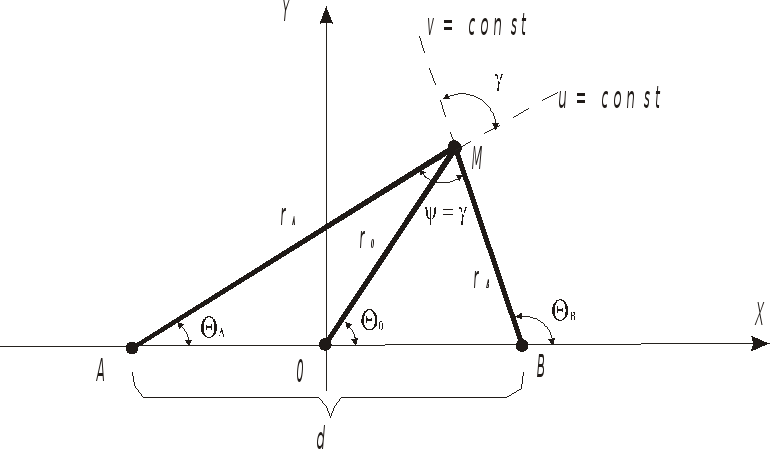
Определим положение ИРИ в географической системе координат.

На рисунке 2 приведены геометрические построения, поясняющие определение координат x и y пеленгуемого ИРИ, при наличии двух станций БС и МС имеющих известные координаты x₁ , y₁ и x₂ , y₂.

Рисунок 2 – Определение координат пеленгуемого ИРИ двумя станциями БС и МС

По результатам обработки радиосигнала от ИРИ измерительные модули определяют направления пеленга – азимуты θ₁ и θ₂, на ИРИ.

Из рисунка 2 следует:

; ; .

Из этих выражений после преобразований получим формулы для расчета координат x и y источника излучения.

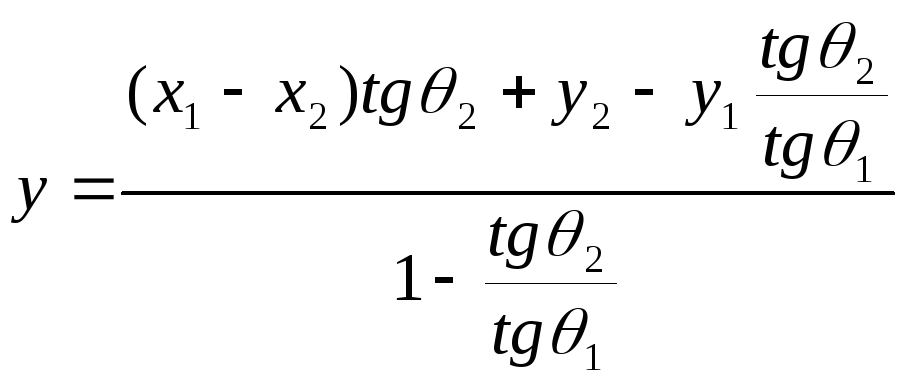, (1)

. (2)

Начало координат выберем на пересечении улицы «Революционная» и улицы «Гагарина».

Пусть имеем две станции БС и МС в районе улиц «Клиническая» и «Победа», с координатами (-8,5;7,5) и (18,5;-11) соответственно (рисунок 3).

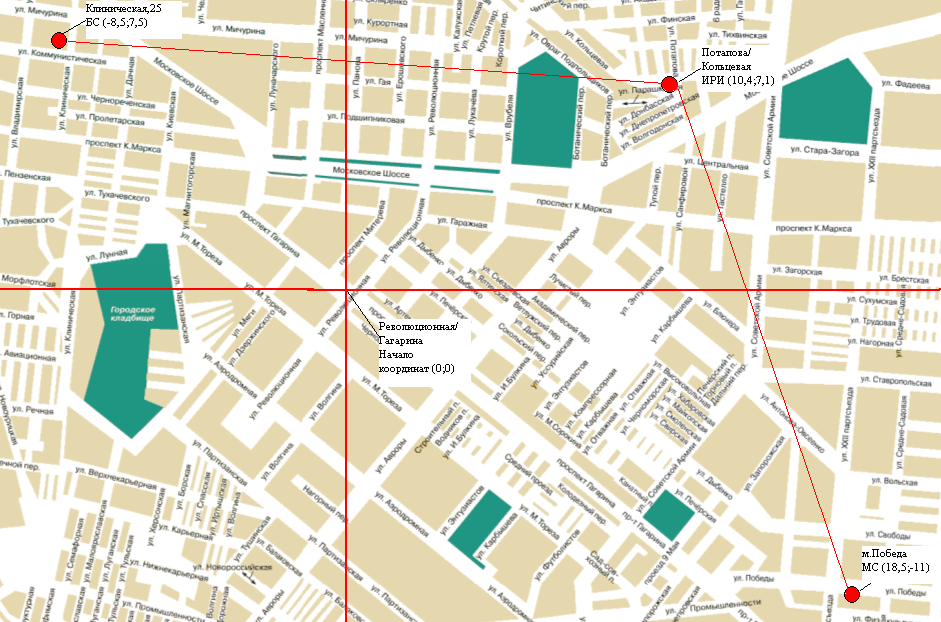
Рисунок 3. Определение координат ИРИ при двух станциях на примере

г. Самары

Азимуты, определенные БС и МС (θ₁ и θ₂) равны -10˚ и 120^˚ соответственно. Рассчитаем координаты x и y ИРИ.

Согласно карте, полученные координаты ИРИ (10,4;7,1) – это положение абонента в районе пересечения улицы «Потапова» и «Кольцевая».

Определим среднеквадратичную ошибку местоопределения по формуле:

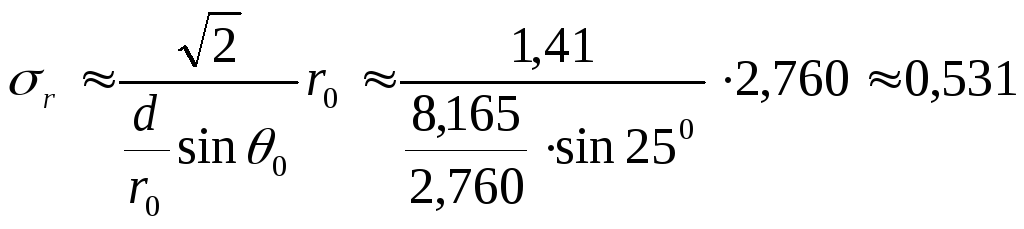
6. Расчет эллипса вероятного местонахождения радиостанции позиционируемой двумя приемными пунктами

При совместной работе двух пеленгаторов с одинаковой мерой точности большую полуось эллипса и, следовательно, максималь­ную линейную ошибку можно вычислить по формуле

,

где — длина большой полуоси эллипса — максимальная ли­нейная ошибка;

—степень надежности пеленгования, т. е. вероятность

нахождения пеленгуемого объекта внутри эллипса;

d — расстояние между пеленгаторами;

К— мера точности;

m — длина медианы, т. е. расстояние между точкой пересе­чения пеленгов и средней точкой базы пеленгаторов;

—угол, образованный медианой и линией базы

ИРИ находится на перпендикуляре к середине базы.

База (d) равна 10 км.

Мера точности (К) равна 30.

Степень надежности пеленгования, т.е. вероятность нахождения пеленгуемого объекта внутри эллипса () равна 0,5, 0,7, 0,8, 0,9, 0,99.

Угол, образованный медианой и линией базы, () равен 90˚.

Для случая

(1)

Для случая

(2)

Когда пеленгуемая радиостанция находится на окружности, построенной радиусом, равным половине базы, т. е. при

(3)

Малая полуось эллипса определяется по формуле

,

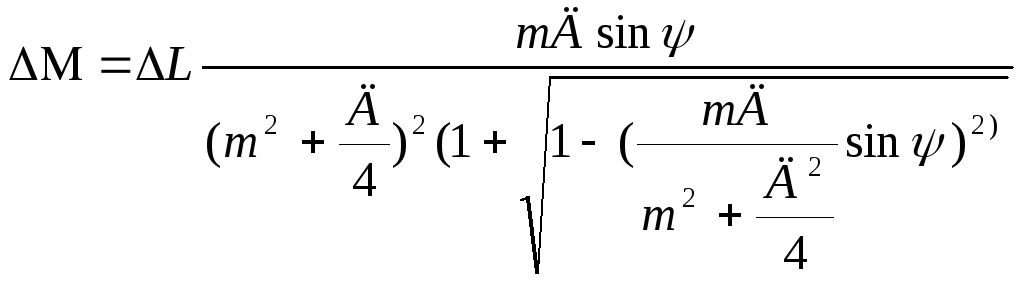где - малая полуось эллипса, т. е. минимальная линейная ошибка.

Если пеленгуемый объект находится на перпендикуляре, по­строенном от середины базы, т. е. когда, то

(4)

при

(5)

при

Если при этом , эллипс превращается в окружность, поскольку

(6)

По результатам расчетов данных построим эллипсы, характеризующие ошибки пеленгования.

Расчет эллипса при угломерном методе позиционирования.

= 75˚

d = 8,165 км

К = 30

= 0,7

m = 4,4

, км

, км

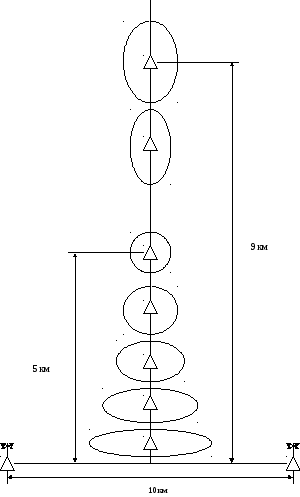
Для того чтобы наглядно представить, как изменяются размеры и конфигурация эллипса в зависи­мости от расстояния до пеленгуемого объекта, рассмотрим случай, когда объект находится на перпендикуляре от середины пеленгаторной базы.

Зададимся вероятностью Рэ = 0,9; величиной базы пеленгования d —10 км; мерой точности пеленгатора К = 30.

По формулам (1), (2), (4) и (5) вычислим значение полуосей эллипса для разных расстояний т, т. е. для разных по­ложений объекта пеленгования.

Результаты расчета приведены в таблице 1 и на рисунке 1.

Таблица 1. Значения полуосей эллипса

m, км	1	2	3	4	5	6	7	8	9
∆L, км	0,187	0,209	0,245	0,295	0,358	0,435	0,374	0,449	0,535
∆M, км	0,936	0,522	0,408	0,369	0,358	0,348	0,267	0,281	0,297