
- •Расчет производительности серии мельниц при изменении их диаметра (2 способа)
- •2 Способ:
- •Результаты расчета:
- •Задача № 3 Задача № 3. Пересчеты составов силикатных материалов
- •Решение задачи
- •Задача № 4 Задача № 4. Расчет свойств многокомпонентных составов
- •Блок-схема:
- •Решение задачи
- •Задача № 5 Домашнее задание. Задача № 5. Расчет свойств многокомпонентных составов
- •Решение задачи
- •Задача № 6 Задача № 6. Простые операции над матрицами
- •Решение задачи
- •Задача № 7 Задача № 7. Перемножение двух матриц
- •2. Таблица замены переменных
- •3. Блок-схема:
- •Текст программы:
- •Решение задачи
- •Задача № 8 Задача № 8. Расчет многокомпонентных шихт для синтеза силикатных материалов. Расчет системы линейных уравнений методом обращения матриц.
- •2.Таблица замены переменных
- •3. Блок-схема:
- •Решение задачи
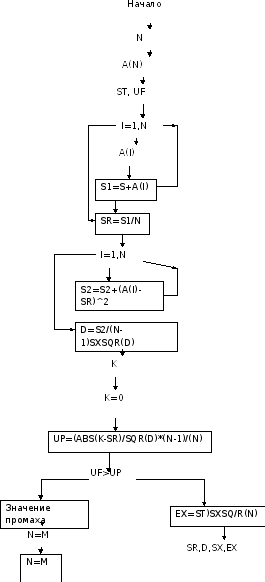
- •Задача № 9 Задача № 9. Количественный статистический анализ результатов эксперимента.
- •2.Таблица замены переменных
- •3.Блок-схема:
- •4.Текст программы:
- •Решение задачи
- •Задача № 10. Расчет коэффициент корреляции
- •Задача № 11. Подбор коэффициентов для различных типов зависимостей.
2.Таблица замены переменных
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Блок-схема:
4.Текст программы:
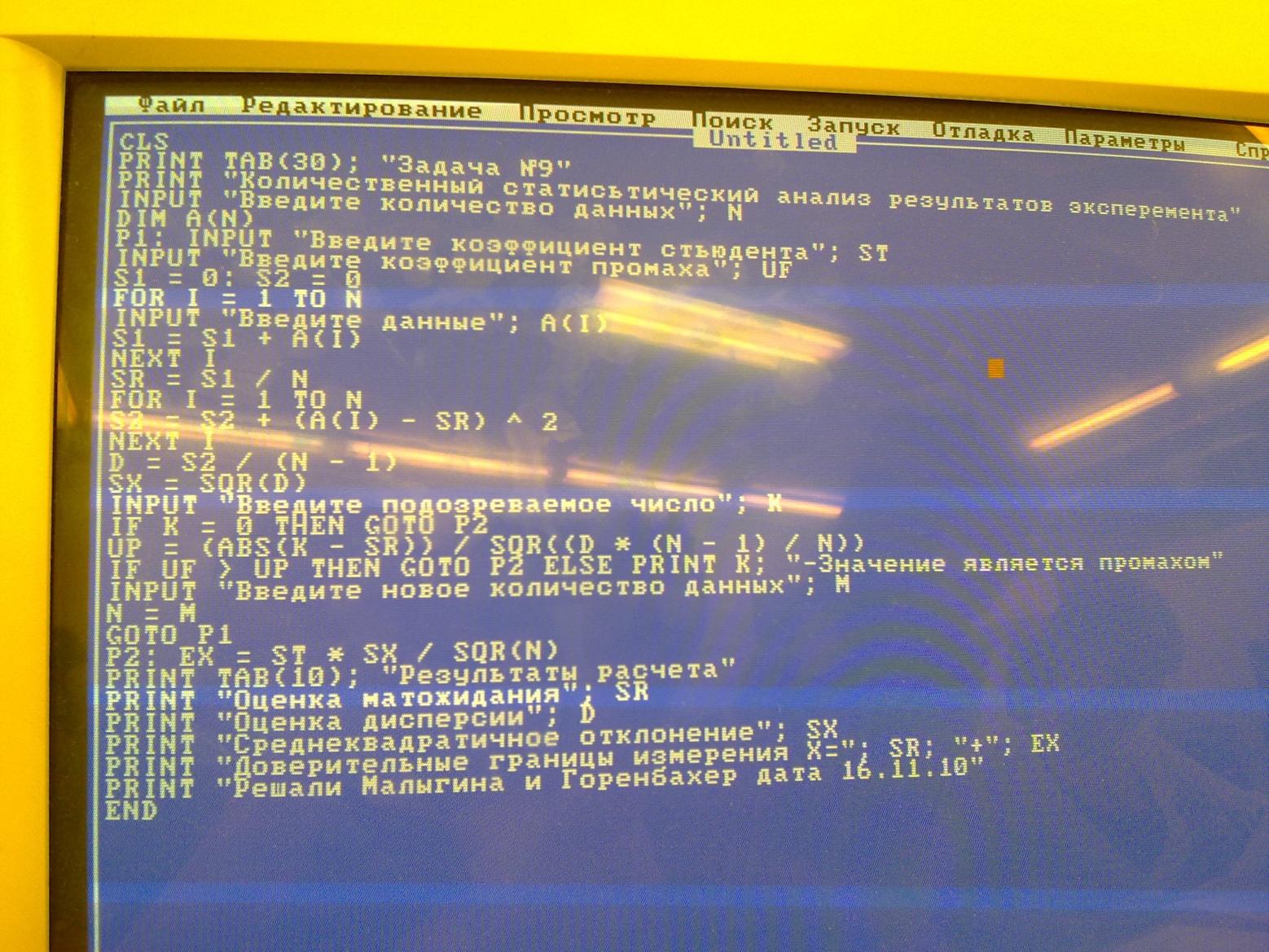
END
Решение задачи
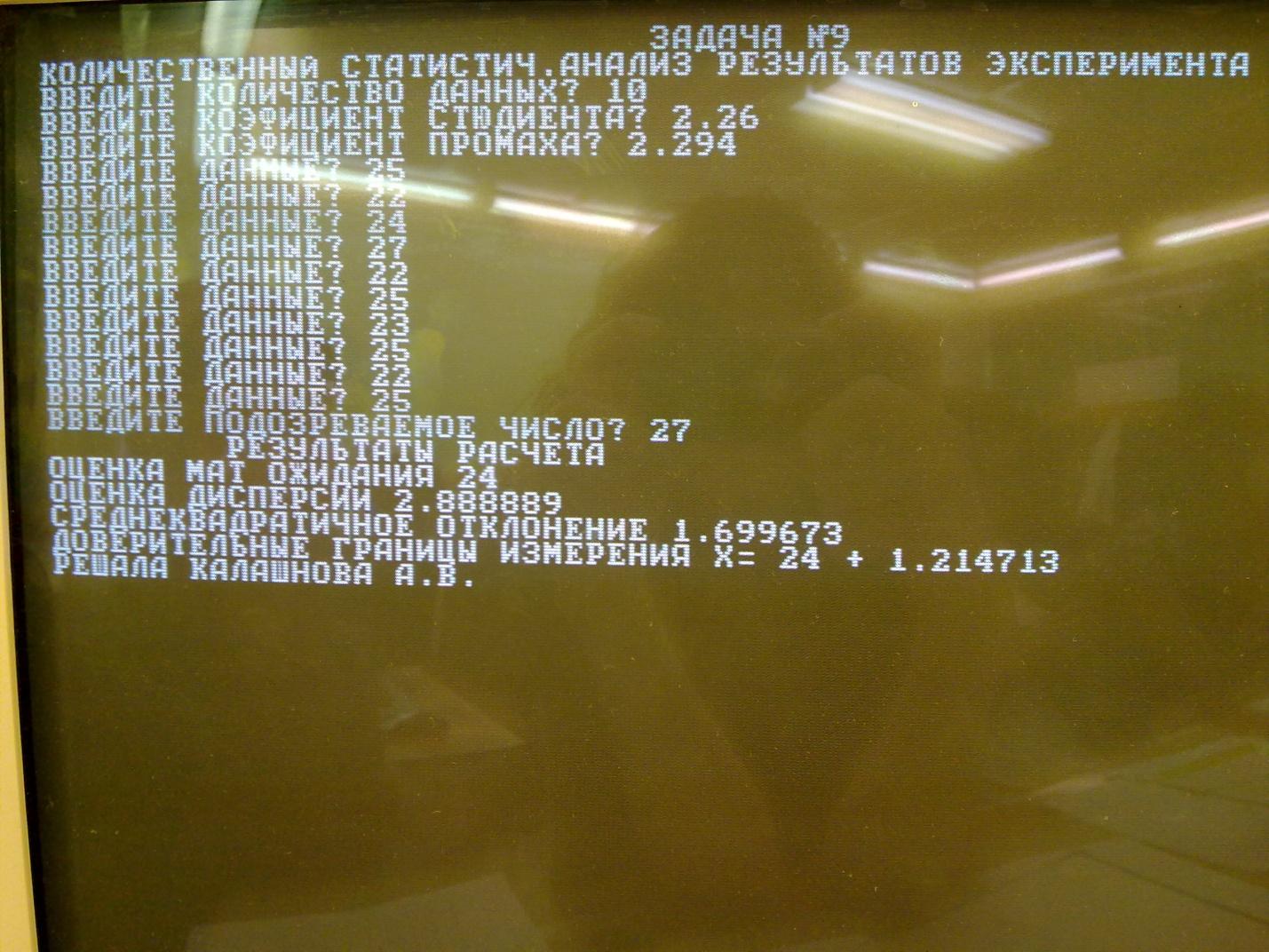
Вывод: В ходе работы я рассчитала среднее значение, дисперсию, среднеквадратичное отклонение, проверила одно из значений (выделено жирным шрифтом) на промах, рассчитала доверительные границы измерения х=24+1,214713
Задача № 10. Расчет коэффициент корреляции
Степень связанности двух величин x и y может быть измерена коэффициентом линейной корреляции. Пусть мы получаем выборочные значения величины xi и соответствующие им значения yi, причем это не последовательные измерения одного и того же значения x и y, а измерения при различных условиях опыта. По измеренным значениям можно построить коэффициент линейной корреляции
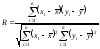 .
.
Если R близко к нулю, то между величинами x и y не существует линейной зависимости, если R=1, то данные полностью коррелированны. Если R>0.95, то связь между переменными функциональная. Положительное значение коэффициента корреляции говорит о прямой связи величин x и y (т.е. при увеличении x увеличивается y и наоборот), отрицательное значение коэффициента корреляции означает обратную связь величин x и y (т.е. при увеличении x уменьшается y и наоборот).
Задание: произвести замену переменных, составить блок-схему алгоритма, написать программу и, используя исходные данные, приведенные в таблице 1, рассчитать коэффициент корреляции для 12 пар значений, сделать выводы.
Таблица 1 – Экспериментальные значения величин x и y
|
№ варианта |
Значения |
|||||||||||||
|
4 |
x |
4,31 |
4,86 |
4,87 |
5 |
4,42 |
4,02 |
4,57 |
4,39 |
4,45 |
4,24 |
4,95 |
4,32 |
|
|
y |
23 |
13,2 |
13 |
10 |
20 |
27 |
18 |
22 |
19 |
24 |
11 |
22,5 |
||
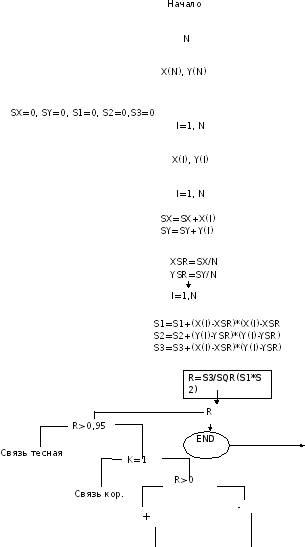
Алгоритм решения:
CLR
PRINT TAB(30); “Задача 10”
PRINT “Расчет коэффициента корреляции”
INPUT “Введите число опытов”; N
DIM X(N), Y(N)
S1=0, S2=0, S3=0, SX=0,SY=0
PRINT “Вводим пары”
FOR I=1 TO N
PRINT I; “-ое значение Х”;
INPUT X(I)
PRINT I; “-ое значение Y”;
INPUT Y(I)
NEXT I
FOR I=1 TO N
SX=SX+X(I)
SY=SY+Y(I)
NEXT I
XSR=SX/N
YSR=SY/N
FOR I=1 TO N
S1=S1+((X(I)-XSR)*(X(I)-XSR)
S2=S2+((Y(I)-YSR)*(Y(I)-YSR)
S3=S3+((X(I)-XSR)*(Y(I)-YSR)
NEXT I
R=S3/SQR(S2*S1)
PRINT TAB (10); “Результаты расчетов”
PRINT “коэффициента корреляции R= ”;
PRINT USING “#,###”; R
IF ABS(R) > 0,95 THEN PRINT “Связь дост. тесная” ELSE PRINT“Связь не дост. тесная”
IF R=0 THEN PRINT “Данные не коррел.”
IF R=1 THEN PRINT “ Связь функционирует”
IF R>0 THEN PRINT “ Связь положительная” ELSE PRINT “Связь отрицательная”
END
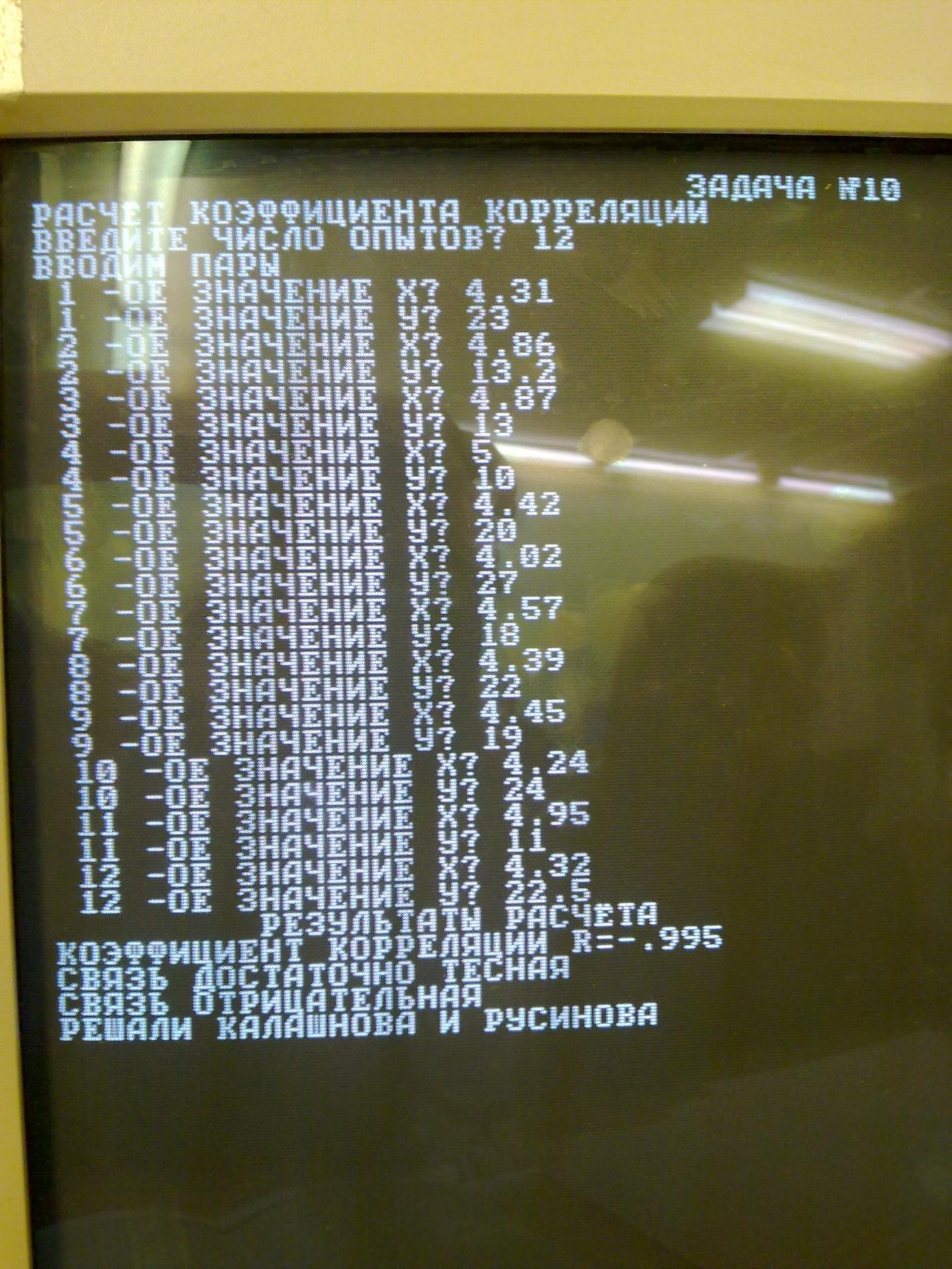
Вывод: В результате работы я определила коэффициент корреляции равный R=-0,990
