Лабораторная работа №2

Тема: Составление и отладка линейных программ.

Цель: Овладеть навыками программирования вычислительных процессов линейной структуры. Закрепить навыки по тестированию и отладке программ.

Теория:

Линейные алгоритмы.

Предполагается следование блока в том же порядке, в каком до того выполнялись предписываемые ими действия. Такой порядок действий называется естественным.

Задача:

Известны стороны треугольника.

Найти S-?.

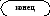
Program pl;

Writeln(‘Введите значения a,b,c’);

Readln(a,b,c);

P=(a+b+c)/2;

S=Sqrt(p*(p-a)*(p-b)*(p-c))

Writeln(’S=’,S:6:3);

End.

Задание: Составление, редактирование и отладка линейных программ. Работа по индивидуальным заданиям.

Задание 1

В1.

Найти объём куба и площадь его боковой поверхности, если задана длина ребра куба.

В2.

В окружность радиуса R вписан правильный треугольник. Определить длину его стороны a, площадь S и площадь круга S_o,вписанного в треугольник:

a=R; S=; S_o=

В 3.

Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.

В4.

Вычислить высоты треугольника по сторонам a,b,c.

В5.

Даны действительные числа x,y,z. Вычислить:

В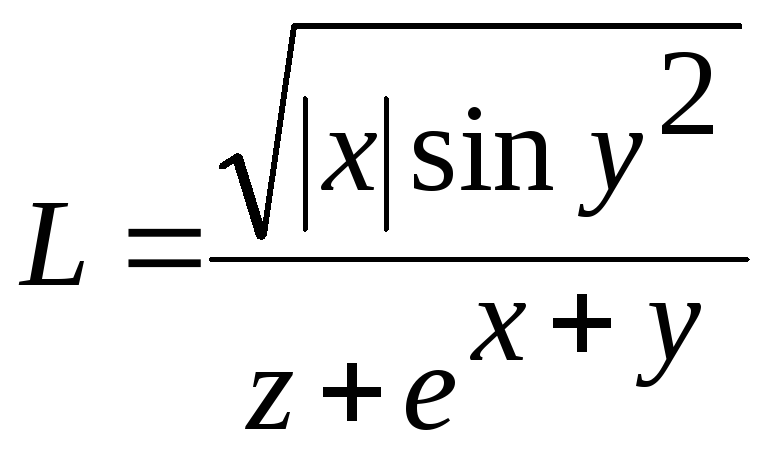 6

Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

В7.

Написать программу вычисления значения меньшей из двух величин a и b, используя формулу:

В8.

Составить программу вычисления корней квадратного уравнения.

В9.

Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.

В10.

Дана сторона равностороннего треугольника. Найти его площадь.

В11.

Вычислить координаты центра тяжести трёх материальных точек с массами

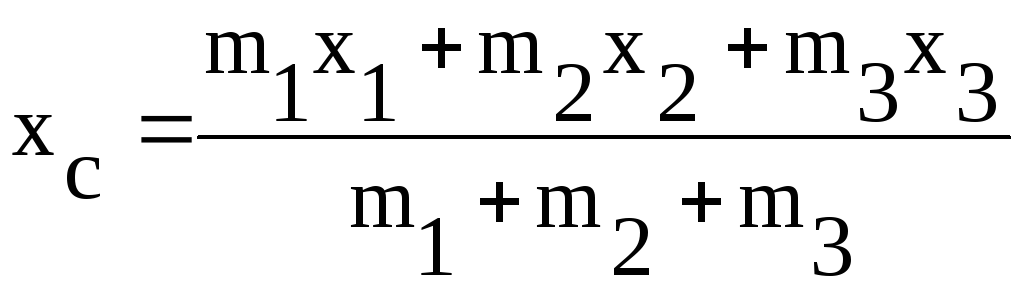
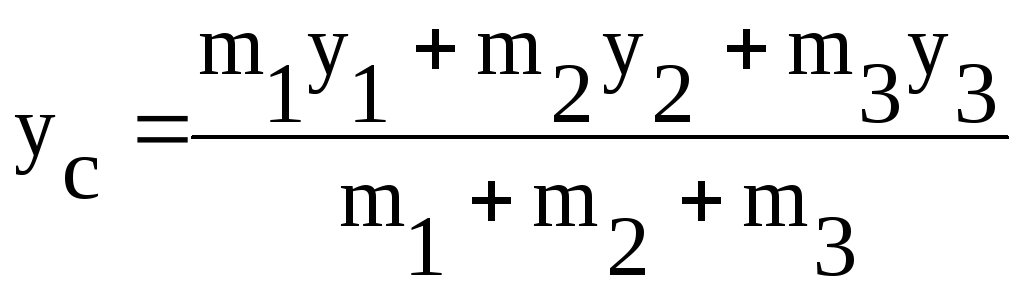и координатами по формулам:

В12.

Треугольник задан координатами вершин. Найти периметр треугольника.

В13.

Определить время падения камня на поверхность земли с высоты h.

В14.

Вычислить расстояние между двумя точками с координатами

В15.

Найти площадь равнобочной трапеции с основаниями a и b и углом  при большем основании.

В16.

Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.

В17.

Для треугольника с заданными координатами вершины

найти радиус вписанной и описанной окружности.

В18.

Треугольник задан величинами своих углов и радиусом описанной окружности.

Написать программу вычисления сторон треугольника.

В19

Вычислить значения выражения

В20.

В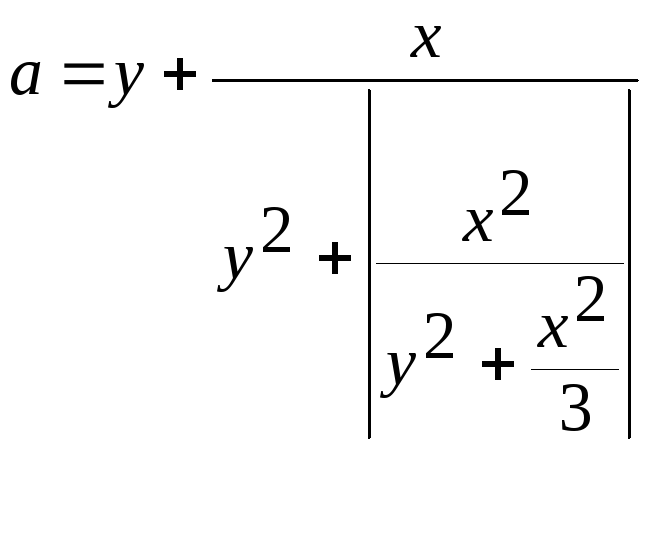ычислить значения выражения:

Задание 2

В1.

В2.

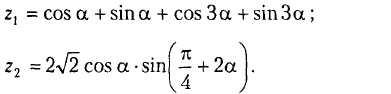
В3.

В4.

В5.

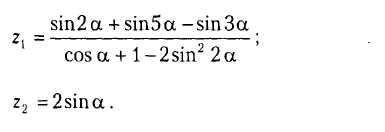
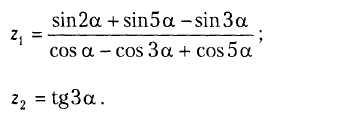
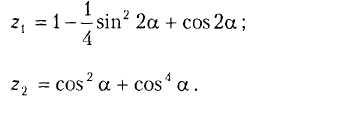
В6.

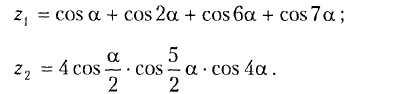
В7.

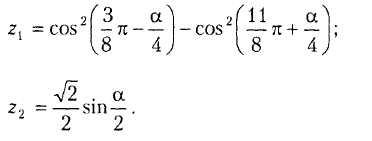
В8.

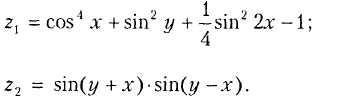
В9.

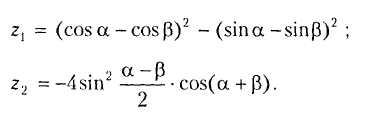
В10.

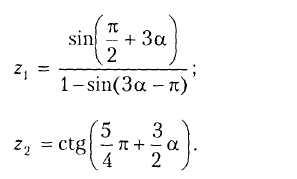
В11.

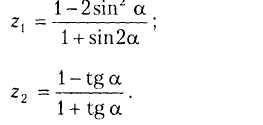
В12.

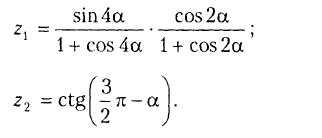
В13.

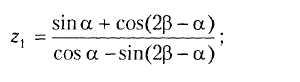
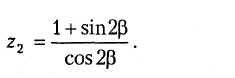
В14.

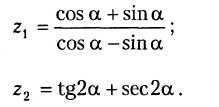
В15.

В16.

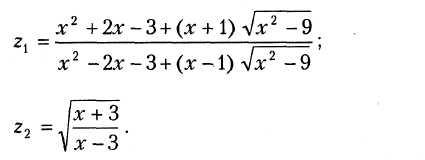
В17.

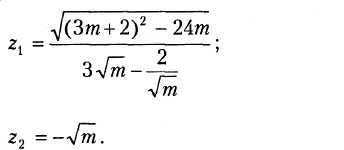
В18.

В19.

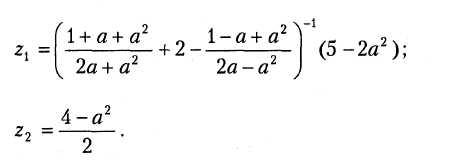
В20.

Лабораторная работа №3

Тема: Составление, редактирование и отладка разветвляющихся программ.

Цель: Овладеть навыками программирования вычислительных процессов разветвляющейся структуры.

Теория:

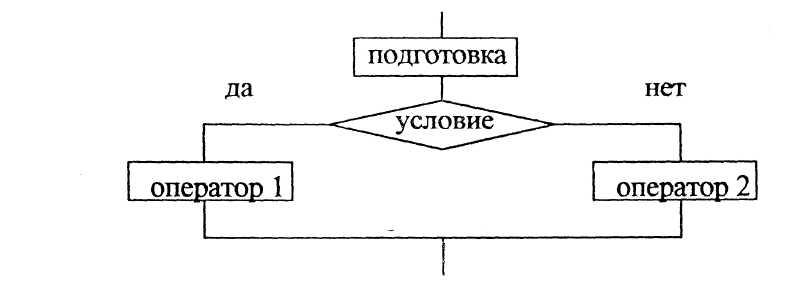
Алгоритмы с разветвленной структурой.

В большинстве вычислительных процессов мы сталкиваемся с тем, что, выбор хода дальнейших вычислений определения предыдущим результатом. Более точно можно сказать что, вычислительный процесс разбивается на ряд этапов и периодов от одного этапа к другому осуществляется при выполнении некоторого условия. Проверка выполнения этих условий тоже может рассматриваться, как некоторый этап вычислительного процесса.

Такие задачи состоят:

а) из общей части;

б) анализ логического уровня;

в) в зависимости от результата анализа - расчёт по той или иной формуле.

Схема разветвления