2. Понятие линейного оператора

В линейной алгебре термины отображение (преобразование) и опера-тор равнозначные.

Следовательно, линейный оператор – это линейное отображение ли-нейного пространства в себя.

Условия а) и б) линейности отображения делают удобной форму за-писи линейного оператора в виде как своеобразное «умножение ли-нейного оператора на вектор».

При такой записи условие а) можно интерпретировать как свойство дистрибутивности такого «умножения», а условие б) – как свойство ассо-циативности:

.

Нарушение любого из этих условий означает, что отображение (опе-ратор) не является линейным.

Рассмотрим примеры типовых линейных операторов.

1. Оператор, переводящий любой вектор линейного пространства R в нулевой вектор пространства , является линейным оператором. Та-кой оператор называется нулевым.

2. Оператор , который каждому вектору пространства R ставит в соответствие сам вектор , является линейным и называется единичным

или тождественным оператором. По условию имеем равенство .

3. Растяжение (сжатие) векторов пространства R в одно и то же число k раз является также линейным оператором. Такой оператор называется оператором подобия, т.е. .

Для этого оператора докажем его линейность. Применим оператор к вектору

.

В результате получим

откуда видно, что условие линейности (2) для данного оператора выполня-ется.

4. Оператор , который каждый вектор поворачивает вокруг некоторой точки 0 в одну и ту же сторону на угол α , является линейным и называется оператором вращения.

Если из пространства Х в пространство Y действует некоторый линейный оператор, то множество образов всех векторов из Х называют областью значений .

Область значений оператора является подпространством в Y . Размер-ность этого подпространства называется рангом оператора .

3. Матрица линейного оператора

Для простоты рассмотрения вопроса выберем реальное трехмерное пространство V₃ с фиксированным базисом и применим к каждому из базисных векторов некоторый линейный оператор . Тогда векторы представляющие собой соответственно образы векторов , имеют в этом базисе разложения

(3)

В этом случае квадратную матрицу третьего порядка

(4) называют матрицей линейного оператора в базисе .

В этой матрице первый столбец состоит из координат образа базис-ного вектора , второй столбец – из координат образа базисного векто-

ра , третий столбец – из координат образа базисного вектора .

Фактически здесь рассмотрен переход от одного базиса линей-ного пространства V₃ к другому его базису . Из того, что линей-ный оператор определяется заданием образов векторов базиса, вытекает, что такой переход является линейным оператором и матрицей такого опе-ратора в данном базисе будет матрица перехода от первого базиса ко вто-рому.

В общем случае каждому линейному оператору, действующему в соответствует линейное преобразование координат произвольного вектора этого пространства. Такое преобразование обычно записывается в матричной форме

, (5) где - координаты вектора , а - координаты вектора – образа при применении линейного оператора .

На основании этого можно найти матрицы рассмотренных типовых линейных операторов (в случае пространства с произвольным бази-сом).

1. Матрицей нулевого оператора независимо от выбора ба-зиса является нулевая матрица соответствующего типа.

Действительно, образом любого вектора в случае нулевого оператора есть нулевой вектор. Поэтому матрица нулевого оператора в любом базисе должна состоять из нулевых столбцов.

2. Матрица Е единичного оператора является единичной матрицей

Действительно, согласно определению единичного вектора координаты векторов и в произвольном базисе должны быть связаны соотношениями:

(6)

На основании (5) запишем уравнение в матричной форме

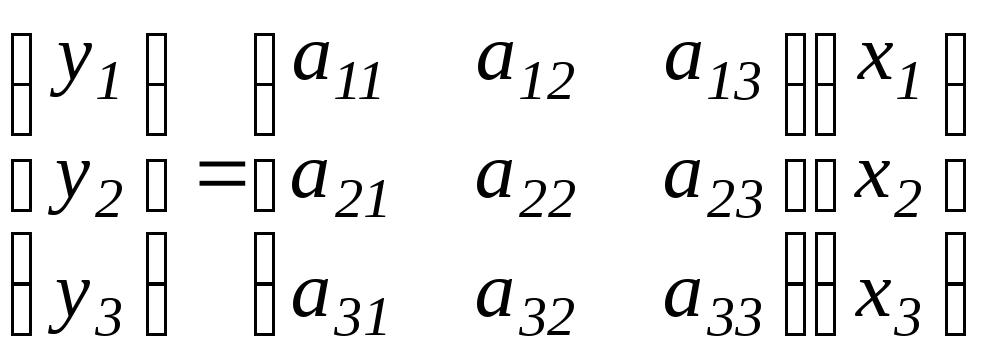(7)

С учетом правила умножения матриц получим

(8)

Эти равенства справедливы, когда будут выполнены соотношения (6), т.е.

Отсюда следует, что матрица единичного оператора является единич-ной.

3. Матрицей оператора подобия (пусть ) будет матрица

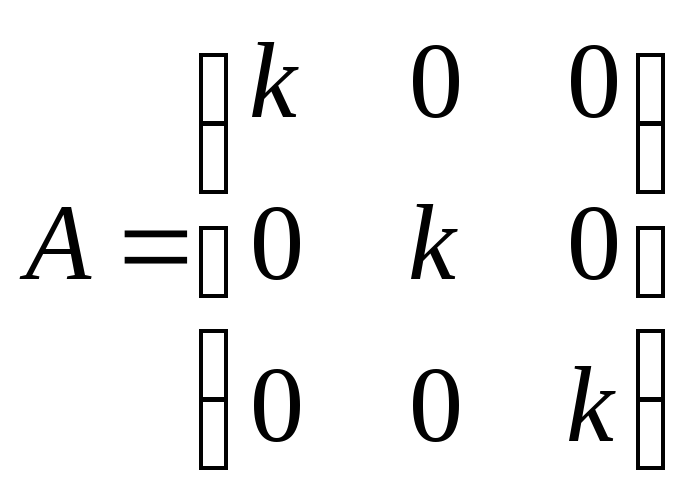
4. Матрицей оператора вращения , действующего в пространстве , будет матрица

Рассмотрим один из подходов к нахождению матрицы нетипового ли-нейного оператора.

Пример 1. В пространстве с базисом линейный оператор переводит векторы соответственно в векторы . Найти матрицу оператора в данном базисе.

Решение. Пусть - матрица оператора . Тогда из условий и по формуле (7) имеем (применительно к пространству )

и .

Используя правило умножения матриц, получим следующую систему уравнений

или

Отсюда имеем .

Следовательно, искомая матрица линейного оператора, действующе-го в пространстве

.