
- •1.Основні гіпотези і співвідношення теорії пружності
- •2. Основні рівняння теорії пружності. Розвязання задачі теорії пружності в переміщеннях (рівняння Ляме).
- •2.2 Розв’язання задач теорії пружності в переміщеннях
- •3.Основні рівняння теорії пружності. Розвязання задачі теорії пружності в напружності(р-ня Бельтрамі-Мічела).
- •2.3 Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
- •4. Плоска задача теорії пружності декартових координатах. Плоска деформація та узагальнений напружений плоский напружений стан.
- •6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
- •Функція Ері
- •7. Розвязок плоскої задачі теорії пружності в поліномах
- •9.Плоска задача теорії пружності в полярних координатах.
- •12.Розрахунок нескінченного клина на дію зосередженого моменту
- •14. Розрахунок балки-стінки методом кінцевих різниць(метод Сіток)
- •3.6 Розрахунок балки-стінки
- •15.Основні гіпотези які приймаються при розрахунках пластин на згин. Класифікація пластин.
- •17. Згин гнучких пластнн, гіпотези, запис рівнянь сумісності деформацій та рівноваги.
- •18.Згин тонких жорстких пластин.Основне диференціальне рівняння згину пластин(вивести р-ня Софі-Жернен-Лагранджа)
- •19. Тонкі гнучкі пластини. Запис граничних умов
- •20. Рівняння ососиметричного згину кільцевих пластин. Запис граничних умов.
- •21.Рівняння осесиметричного згину круглих пластин,запис граничних умов.
- •5.11 Основні рівняння вигину круглої пластинки
- •22. Тонкі жорсткі пластини, циліндричний згин пластин.
- •24.Поперечний згин вільно опертих пластин(розвязок Навє в подвійних тригонометричних рядах).
- •25. Поперечний згин пластин, дві протилежні сторони яких шарнірно оперті (рішення м. Леві в одинарних тригонометричних рядах).
- •26. Розрахунок пластин, які працюють на згин, методом скінченних різниць (метод сіток). Запис граничних умов.
- •27. Варіаційні методи розрахунку пластин на згин.
- •28.Оболонки. Класифікаці оболонок. Безмоментна теорія розрахунку оболонок.
- •30. Розрахунок тонкостінних резервуарів. Вивести формулу Лапласа.
- •6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
- •Функція Ері
- •12.Розрахунок нескінченного клина на дію зосередженого моменту
6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
Розв’язання плоскої задачі є одним з найважливіших питань прикладної теорії пружності. Пояснюється це тим, що дуже багато конструкцій або їхніх елементи працюють в умовах плоского напруженого стану або плоскої деформації, що й розглядається в плоскій задачі теорії пружності.
Плоский напружений стан виникає в тонкій пластинці, що по торцевих сторонах навантажена силами, паралельними її основам, і рівномірно розподіленими по товщині (рис)
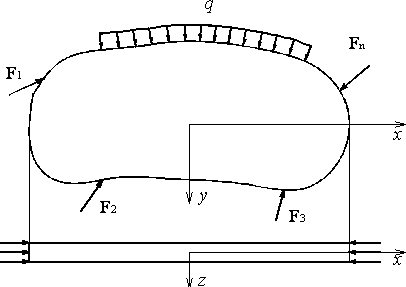
Розвяхок плоскої задачі в напруженнях


При
 похідні від них будуть=0.
похідні від них будуть=0.
Функція Ері

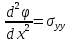








7. Розвязок плоскої задачі теорії пружності в поліномах
В більшості випадків розв’язок плоскої задачі зводиться до знаходження функції напружень (функції Ері), яка підкоряється бігармонічному рівнянню:
![]()
і задовольняє граничним умовам на контурі диску
qx= σxx ∙nx + τxx∙ny
qy = τyx∙nx+ σyy∙ny,
де qx,qy– складові зовнішньго навантаження в точці контуру
nx ,ny - напрямні косинуси зовнішньої нормалі в даній точці контуру.
Напруження визначаються через функцію Ері такими співвідношеннями :
Під час розв’язку плоскої задачі функцію напружень часто задано, поряд з іншими виразами вона може бути у вигляді полінома.Таким чином, поліном 2,3,4,5 ступеня є бігармонічною функцією й може бути застосований до рішення плоскої задачі.За допомогою алгебраїчних поліномів можна вирішити, ряд простих задач: задача про чистий згин балки, згинанні балки на двох опорах під дією рівномірно розподіленого навантаження тощо.
9.Плоска задача теорії пружності в полярних координатах.
При рішенні плоскої задачі зустрічаються тіла, обмежені поверхнями кругового циліндра і радіально розбіжними площинами. У цих випадках перехід від декартовой системи координат до полярної значно спpощує рішення.
Виріжемо
із пластинки товщиною, рівною одиниці,
елемент ![]() (рис.
4.1). Для цього проведемо радіус
(рис.
4.1). Для цього проведемо радіус ![]() під
довільним кутом
під
довільним кутом ![]() до
початкового радіус-вектору, потім дамо
куту нескінченно мале збільшення
до
початкового радіус-вектору, потім дамо
куту нескінченно мале збільшення ![]() й
проведемо радіус
й
проведемо радіус ![]() . Довільним
радіусом
. Довільним
радіусом ![]() проведемо
дугу
проведемо
дугу ![]() , потім
дамо радіусу
, потім
дамо радіусу ![]() збільшення
збільшення ![]() й
проведемо другу дугу —
й
проведемо другу дугу — ![]() .
Сторони отриманого елемента мають
наступні розміри:
.
Сторони отриманого елемента мають
наступні розміри:
![]() ,
, ![]() ,
, ![]() .
.

Основні рівняння :
диференціальні рівняння рівноваги
![]()
Особливістю
цих рівнянь у порівнянні з умовами
рівноваги для плоскої задачі в декартових
координатах є наявність у знаменнику
величини ![]()
рівняння нерозривності деформацій:
![]()
Розгорнуте рівняння нерозривності деформацій:
![]()
Рівняння коші:

Формули закону Гука для узагальненого плоского напруженого стану в полярних координатах зберігають такий же вид, як і в декартовій системі
|
10. Осесиметрична плоска задача. Розрахунок тонкостінних циліндрів.
Зупинимося
на плоских задачах, у яких напруження,
а, отже, і функція
або після диференціювання
Також спрощуються вираз напружень (4.24):
При відсутності об'ємних сил залишиться тільки одне з рівнянь рівноваги (4.1)
Спростяться й геометричні співвідношення Коші (4.4), тому що складова переміщення v в силу симетрії дорівнює нулю:
З формул закону Гука (4.5) залишаться лише дві:
Осесимметричну задачу в переміщеннях можна вирішити в загальному виді. З формул закону Гука (а) знаходимо
За допомогою співвідношень (4.30) виключаємо із цих рівнянь складові деформації:
Підставляючи
ці напруження в рівняння рівноваги
(4.29), одержуємо диференціальне рівняння
відносно складового переміщення
Воно має змінні коефіцієнти. Для рішення приведемо його до рівняння з постійними коефіцієнтами за допомогою наступної підстановки:
або
Диференціюючи
вираз (4.32) по змінній
Встановимо
зв'язок між похідними функції
З урахуванням рівності (г) одержуємо
Друга похідна
Підставляючи похідні (д) і (е) в рівняння (4.31), знаходимо
Рішення цього рівняння має вигляд
Вертаючись
до старої змінної
Знаючи
складову переміщення
а з формул (б) - складових напружень:
Постійні
При
розгляді довгих циліндричних оболонок
з'являється можливість зневажити в
поперечних перерізах згинаючим
Диференціальні рівняння рівноваги елемента циліндричної оболонки в розглянутому випадку мають такий вигляд:
Система
рівнянь (7.22) шляхом виключення
зусиль S, Q і
де
P — функція, що залежить від складових поверхневого навантаження й обумовлюється формулою
Крім статичних, уводяться також і геометричні гіпотези: поперечні подовження і деформації зсуву в серединній поверхні приймаються рівними нулю як величини, що мало впливають на основні зусилля оболонки:
Складові
переміщення довільної точки серединної
поверхні по напрямках твірної, дотичній
до дуги контурної лінії й зовнішньої
нормалі, позначимо відповідно Тоді складові деформації, відповідно до формул (7.10), приймуть вид
Виключимо з формул (в) переміщення. Для цього формули (в) продифференціюємо у такий спосіб:
Складаючи другу й третю формули (г), одержуємо
Звідси, використовуючи п'яту формулу (г), знаходимо
Розглядаючи
спільно першу й четверту формули (г)
і виключая з них
Підставляючи потім похідні (д) і (е) в останню формулу (г), одержуємо диференціальне рівняння нерозривності деформацій:
Використовуючи геометричні гіпотези (б), одержуємо
Диференціальне рівняння (ж) показує, що згинання елементарної поперечної смужки (деформація контуру) супроводжується розтяганням оболонки уздовж твірної (депланація поперечного переріза).
Фізичні
рівняння теорії оболонок можна
представити в спрощеній формі, вважаючи
коефіцієнт Пуассона
Вносячи ці значення в рівняння (ж) і приєднуючи рівняння (а), одержуємо систему двох спільних диференціальних рівнянь
Тут
напруження
При
з яких перші залежать тільки від змінної s, а другі — від змінної x. Одна із двох функцій приблизно задається, а друга визначається з диференціальних рівнянь.
В.
3. Власов запропонував задаватися
функцією
де l — довжина оболонки в напрямку твірної; m — довільний параметр.
Це
рівняння разом із граничними умовами
на криволінійних краях оболонки в
кожному конкретному випадку крайової
задачі буде давати систему ортогональних
фундаментальних функцій
Якщо
обидва криволінійних краї жорстко
затиснені, то при
де Для оболонки, у якої один край шарнірно обпертий, а іншої - жорстко затиснений, граничні умови мають вигляд
при і фундаментальні функції приймають такий вид:
де Подібним чином будуються фундаментальні функції і при інших граничних умовах. Фундаментальні функції, отримані зазначеним шляхом, а також їх другі похідні мають властивість ортогональності:
Для відшукання функцій змінної представляємо їх разом з функцією (7.24) у вигляді нескінченних рядів:
Помножуючи
перше рівняння (7.25) на
Тут
При інтегруванні системи (7.27) з'являться вісім довільних постійних. Для їх визначення використовуються граничні умови на поздовжніх краях оболонки. Число цих умов у кожній точці одного краю дорівнює чотирьом. Ці умови можуть бути статичними, геометричними і змішаними. Таким чином, задача про рівновагу довгої циліндричної оболонки при будь-яких заданих граничних умовах і при дії довільного навантаження повністю розв'язне. 11. Розрахунок нескінченного клина на дію зосередженої сили.
Початок
системи координат вибираємо на вістрі
клина. Клин обмежується двома гранями,
які повернуті відносно осі х на кути
α1 і α2. Довільна точка клина має
координати r
і γ,
де α1≤ γ
≤α1. Кут між лінією дії сили і віссю х позначаємо β. Кути β, γ, α1 і а2- додатні, якщо відраховуються від осі х протиходугодинникової стрілки . Функція напружень для даної задачі має вигляд:
Вона
задовольняє рівнянню
Такий напружений стан наз. Простим радіальним. Але одержана формула для визначення радіальних напружень досить громіздка, тому в більшості випадків доцільно користуватися частинними випадками. а) Сила діє вздовж бісектриси кута.
В
полярній системі координат:
В декартовій системі координат:
|
|







 і граничним умовам
і граничним умовам
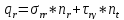
 В
відповідності до виразів: напруження
дор.:
В
відповідності до виразів: напруження
дор.:




