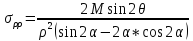- •1.Основні гіпотези і співвідношення теорії пружності
- •2. Основні рівняння теорії пружності. Розвязання задачі теорії пружності в переміщеннях (рівняння Ляме).
- •2.2 Розв’язання задач теорії пружності в переміщеннях
- •3.Основні рівняння теорії пружності. Розвязання задачі теорії пружності в напружності(р-ня Бельтрамі-Мічела).
- •2.3 Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
- •4. Плоска задача теорії пружності декартових координатах. Плоска деформація та узагальнений напружений плоский напружений стан.
- •6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
- •Функція Ері
- •7. Розвязок плоскої задачі теорії пружності в поліномах
- •9.Плоска задача теорії пружності в полярних координатах.
- •12.Розрахунок нескінченного клина на дію зосередженого моменту
- •14. Розрахунок балки-стінки методом кінцевих різниць(метод Сіток)
- •3.6 Розрахунок балки-стінки
- •15.Основні гіпотези які приймаються при розрахунках пластин на згин. Класифікація пластин.
- •17. Згин гнучких пластнн, гіпотези, запис рівнянь сумісності деформацій та рівноваги.
- •18.Згин тонких жорстких пластин.Основне диференціальне рівняння згину пластин(вивести р-ня Софі-Жернен-Лагранджа)
- •19. Тонкі гнучкі пластини. Запис граничних умов
- •20. Рівняння ососиметричного згину кільцевих пластин. Запис граничних умов.
- •21.Рівняння осесиметричного згину круглих пластин,запис граничних умов.
- •5.11 Основні рівняння вигину круглої пластинки
- •22. Тонкі жорсткі пластини, циліндричний згин пластин.
- •24.Поперечний згин вільно опертих пластин(розвязок Навє в подвійних тригонометричних рядах).
- •25. Поперечний згин пластин, дві протилежні сторони яких шарнірно оперті (рішення м. Леві в одинарних тригонометричних рядах).
- •26. Розрахунок пластин, які працюють на згин, методом скінченних різниць (метод сіток). Запис граничних умов.
- •27. Варіаційні методи розрахунку пластин на згин.
- •28.Оболонки. Класифікаці оболонок. Безмоментна теорія розрахунку оболонок.
- •30. Розрахунок тонкостінних резервуарів. Вивести формулу Лапласа.
- •6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
- •Функція Ері
- •12.Розрахунок нескінченного клина на дію зосередженого моменту
6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
Розв’язання плоскої задачі є одним з найважливіших питань прикладної теорії пружності. Пояснюється це тим, що дуже багато конструкцій або їхніх елементи працюють в умовах плоского напруженого стану або плоскої деформації, що й розглядається в плоскій задачі теорії пружності.
Плоский напружений стан виникає в тонкій пластинці, що по торцевих сторонах навантажена силами, паралельними її основам, і рівномірно розподіленими по товщині (рис)
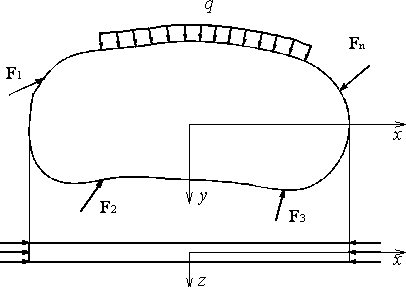
Розвяхок плоскої задачі в напруженнях


При
 похідні від них будуть=0.
похідні від них будуть=0.
Функція Ері










12.Розрахунок нескінченного клина на дію зосередженого моменту
Рішення
плоскої задачі в полярних координатах
у напруженнях полягає у відшуканні
трьох функцій ![]() і
і ![]() , за допомогою
трьох рівнянь: двох рівнянь рівноваги
(4.1) і рівняння нерозривності деформацій
(4.3) при обов'язковому задоволенні умов
на поверхні.
, за допомогою
трьох рівнянь: двох рівнянь рівноваги
(4.1) і рівняння нерозривності деформацій
(4.3) при обов'язковому задоволенні умов
на поверхні.
Аналогічно
тому, як було зроблено при рішенні
плоскої задачі в декартових координатах,
рішення в полярних координатах можна
звести до відшукання однієї функції
напружень ![]() .
Виберемо цю функцію так, щоб напруження
виражалися через неї в такий спосіб:
.
Виберемо цю функцію так, щоб напруження
виражалися через неї в такий спосіб:
|
|
(4.24) |
Підставляючи ці вирази в рівняння рівноваги (4.1), переконуємося, що при відсутності об'ємних сил останні обертаються в тотожності. Щоб перетворити рівняння нерозривності деформацій (4.3), складемо почленно формули для нормальних напружень (4.24)
![]() .
.
Права
частина цієї суми представлена оператором
Лапласа над функцією ![]() .
Отже,
.
Отже,
![]()
і з рівняння (4.3) одержуємо
![]() ,або
,або![]() (4.25)
(4.25)
У розгорнутому виді рівняння нерозривності деформацій (4.25) записується в такий спосіб:
|
|
(4.26) |
Таким чином, функція напружень для плоскої задачі в полярних координатах також повинна бути бігармонічною.
Приймаємо якусь функцію ϕ:

Приймаємо,що дана функція задовольняє граничним умовам і бігармонічному рівнянню.
Запишемо оператор Лапласа в полярній системі координат:


Вирази для напружень в полярній системі координат:



Підставивши функцію і знайшовши похідні,ми отримаємо:



Граничні
умови: ;
;
Підставляємо
граничні умови у
 і виражаємо значення А:
і виражаємо значення А:
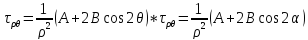 =0
=0

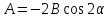
Тоді,в кінцевому випадку отримаємо:



Розглянемо
клин довжиною
 та знайдемо момент відносно точки О:
та знайдемо момент відносно точки О:


dT=dS =
= d
d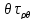
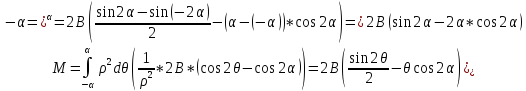
Звідси виражаємо В:
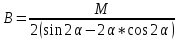
Тоді ,підставивши,значення А і В отримаємо: