
- •1.Основні гіпотези і співвідношення теорії пружності
- •2. Основні рівняння теорії пружності. Розвязання задачі теорії пружності в переміщеннях (рівняння Ляме).
- •2.2 Розв’язання задач теорії пружності в переміщеннях
- •3.Основні рівняння теорії пружності. Розвязання задачі теорії пружності в напружності(р-ня Бельтрамі-Мічела).
- •2.3 Рішення задачі теорії пружності в напруженнях при постійних об'ємних силах
- •4. Плоска задача теорії пружності декартових координатах. Плоска деформація та узагальнений напружений плоский напружений стан.
- •6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
- •Функція Ері
- •7. Розвязок плоскої задачі теорії пружності в поліномах
- •9.Плоска задача теорії пружності в полярних координатах.
- •12.Розрахунок нескінченного клина на дію зосередженого моменту
- •14. Розрахунок балки-стінки методом кінцевих різниць(метод Сіток)
- •3.6 Розрахунок балки-стінки
- •15.Основні гіпотези які приймаються при розрахунках пластин на згин. Класифікація пластин.
- •17. Згин гнучких пластнн, гіпотези, запис рівнянь сумісності деформацій та рівноваги.
- •18.Згин тонких жорстких пластин.Основне диференціальне рівняння згину пластин(вивести р-ня Софі-Жернен-Лагранджа)
- •19. Тонкі гнучкі пластини. Запис граничних умов
- •20. Рівняння ососиметричного згину кільцевих пластин. Запис граничних умов.
- •21.Рівняння осесиметричного згину круглих пластин,запис граничних умов.
- •5.11 Основні рівняння вигину круглої пластинки
- •22. Тонкі жорсткі пластини, циліндричний згин пластин.
- •24.Поперечний згин вільно опертих пластин(розвязок Навє в подвійних тригонометричних рядах).
- •25. Поперечний згин пластин, дві протилежні сторони яких шарнірно оперті (рішення м. Леві в одинарних тригонометричних рядах).
- •26. Розрахунок пластин, які працюють на згин, методом скінченних різниць (метод сіток). Запис граничних умов.
- •27. Варіаційні методи розрахунку пластин на згин.
- •28.Оболонки. Класифікаці оболонок. Безмоментна теорія розрахунку оболонок.
- •30. Розрахунок тонкостінних резервуарів. Вивести формулу Лапласа.
- •6. Плоска задача теорії пружності, розв’язок плоскої задачі в напруженнях, ф-ція напруження Ері.
- •Функція Ері
- •12.Розрахунок нескінченного клина на дію зосередженого моменту
28.Оболонки. Класифікаці оболонок. Безмоментна теорія розрахунку оболонок.
Оболонкою називається тіло, обмежене: двома криволінійними поверхнями, відстань між якими (товщина оболонки h) мала в порівнянні з іншими розмірами. Поверхню, що ділить товщину оболонки навпіл, називається серединною.
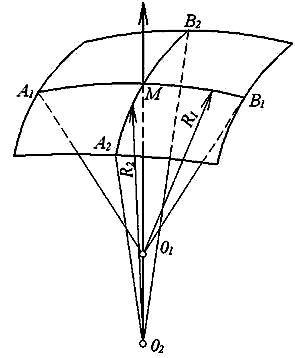
На рис.
показаний елемент серединної поверхні
оболонки. На елементі зображені лінії
перетинання двох взаємно перпендикулярних
площин, нормальних до серединної
поверхні, тобто проходячих через нормаль
. Ці лінії являють собою криві, окреслені
радіусами R1
та R2
. 
 Величини,
зворотні радіусам,
Величини,
зворотні радіусам,
![]() ,
,
![]() називаються кривизнами оболонки.На
серединній поверхні оболонки завжди
можна знайти дві взаємно перпендикулярні
лінії, кривизни яких мають властивості
екстремальності: одна з них максимальна,
а інша — мінімальна. Кривизни, що
володіють властивостями екстремальності,
називаються головними. Вони позначаються
індексами 1 і 2. Геометрія поверхні
оболонки характеризується гаусовою
кривизною,
що являє собою добуток головних кривизн:
називаються кривизнами оболонки.На
серединній поверхні оболонки завжди
можна знайти дві взаємно перпендикулярні
лінії, кривизни яких мають властивості
екстремальності: одна з них максимальна,
а інша — мінімальна. Кривизни, що
володіють властивостями екстремальності,
називаються головними. Вони позначаються
індексами 1 і 2. Геометрія поверхні
оболонки характеризується гаусовою
кривизною,
що являє собою добуток головних кривизн:
![]() Розрізняють оболонки позитивної
гаусової кривизни (сферичні, еліптичні;
рис. 75, а); нульовий гаусової кривизни
(циліндричні, конічні; рис. 75, б); негативної
гаусової кривизни (гіперболічні; рис.
75, в); змішаної кривизни, тобто таких,
що складаються з ділянок з різної
гаусовою кривизною (тороподібні).
Розрізняють оболонки позитивної
гаусової кривизни (сферичні, еліптичні;
рис. 75, а); нульовий гаусової кривизни
(циліндричні, конічні; рис. 75, б); негативної
гаусової кривизни (гіперболічні; рис.
75, в); змішаної кривизни, тобто таких,
що складаються з ділянок з різної
гаусовою кривизною (тороподібні).
![]()
Рис. 7.2. Оболонки різної гаусової кривизни Гаус
Довільне
навантаження викликає в оболонках дві
групи зусиль: 1) нормальні
![]() ,
,![]() і зрушуючи
і зрушуючи
![]() ,
,
![]() сили, що діють у площинах, дотичних до
серединної поверхні (рис. 7.3, а); 2) згинаючі
сили, що діють у площинах, дотичних до
серединної поверхні (рис. 7.3, а); 2) згинаючі
![]() ,
,
![]() і крутні моменти, а також поперечні
сили :
і крутні моменти, а також поперечні
сили :

В інженерній практиці зустрічаються задачі, коли напруги постійні по товщині оболонки й приводяться тільки до зусиль першої групи. Такий напружений стан називається безмоментним. Розрахунок по безмоментній теорії значно простіший ніж розрахунок по повній, моментній теорії. Не стосуючись строгого доказу, умови існування безмоментного напруженого стану можна сформулювати в такий спосіб:
1. Оболонка повинна мати безперервну поверхню, що плавно змінюється.
2. Навантаження на оболонку повинне бути плавним і безперервним.
3. Краї оболонки повинні мати можливість вільно переміщатися в напрямку нормалі до поверхні. Однак граничні умови повинні забезпечувати незмінюваність форми оболонки.
4. Сили, прикладені до країв оболонки, повинні лежати в площині, дотичній до її серединної поверхні.
Залежно
від відношення товщини до найменшого
радіуса кривизни серединної поверхні
оболонки діляться на товсті й тонкі.
Оболонки вважаються товстими, якщо
відношення
![]() і тонкими, якщо
і тонкими, якщо
![]()
30. Розрахунок тонкостінних резервуарів. Вивести формулу Лапласа.
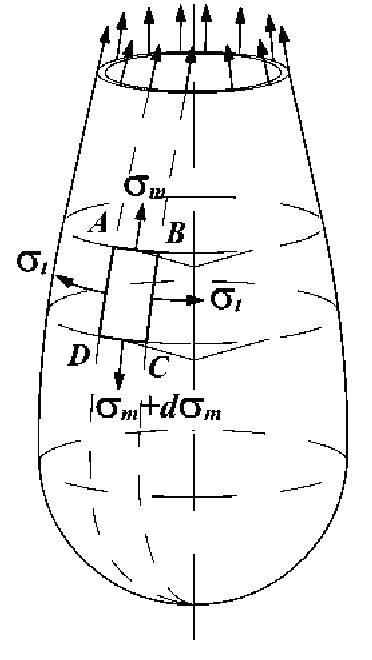
Розглянемо резервуар, що представляє собою
осесиметричну оболонку з товщиною стінки h , навантажену
внутрішнім тиском p .
Меридіональні перерізи оболонки представляють собою
плавні криві без зламів. Перерізи, перпендикулярні осі, – кола.
Край оболонки закріплено так, що в перерізі діють тільки
нормальні напруження.
Зі стінки резервуара виділимо елемент ABCD двома
площинами, що проходять через меридіани, і двома конічними
поверхнями, що пересікають оболонку вздовж паралелей AB ,
CD.
Позначимо:
1 OO – нормаль до
елемента.;
O– центр елемента;
m t ρ ,ρ – радіуси кривизни оболонки в
меридіональному і тангенціальному напрямках.
Прикладемо до елемента зовнішні і
внутрішні сили і запишемо рівняння рівноваги:
сума проекцій сил на нормаль O O 1 дорівнює
нулю:


Поділивши на
 ,
одержимо рівняння Лапласа:
,
одержимо рівняння Лапласа:

