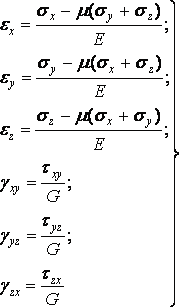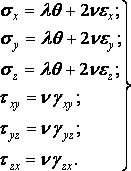1.Основні гіпотези і співвідношення теорії пружності

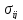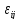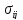Основними поняттями теорії пружності є напруження, що діють на малих площинках, котрі можна уявно провести в тілі через задану точку P, деформації малої околиці точки P і переміщення самої точки P. Точніше кажучи, вводяться тензор механічних напружень, тензор малих деформацій і вектор переміщення u_i. Коротке позначення , де індекси i, j набувають значень 1, 2, 3 (або x,y,z) слід розуміти як матрицю у видах:

=

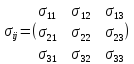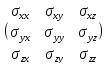
1.Гіпотеза суцільності. Відповідно до цієї гіпотези тверде тіло має

безперервну структуру й ця властивість безперервності відноситься до

будь-якого як завгодно малого об’єму тіла. Таке допущення дозволяє

стверджувати, що напруги, деформації й переміщення є безперервними

функціями координат точок тіла, і для дослідження

напряжено-деформованого стану тіла можна використовувати аналіз

нескінченно малих.

2.Гіпотеза про фізичну однорідність. Відповідно до цієї гіпотези всі

фізичні характеристики тіла (модулі пружності, коефіцієнти Пуассона,

щільності й ін.) не залежать від координат точок тіла.

3.Гіпотеза про природний ненапружений стан. Суть цього твердження

полягає в тому, що при відсутності зовнішніх навантажень напруги у всіх

точках тіла приймаються рівними нулю. Практично ж у тілі можуть бути

початкові напруги, іноді досить значні (наприклад, залишкові зварювальні

напруги).

4.Гіпотеза про ідеальну пружність. Це означає, що форма й розміри тіла

повністю відновлюються після усунення причин, що викликали деформації, а

між деформаціями й напругами існує лінійна залежність, тобто

справедливий закон Гука.

2. Основні рівняння теорії пружності. Розвязання задачі теорії пружності в переміщеннях (рівняння Ляме).

У попередньому розділі отримані три групи формул, які утворять основні рівняння теорії пружності.

1. Статичні рівняння. У цю групу входять диференціальні рівняння рівноваги:

(2.1)

і умови на поверхні:

(2.2)

2. Геометричні  рівняння. У цю групу входять геометричні співвідношення Коші:

(2.3)

і рівняння нерозривності деформацій:

(2.4)

 

3. Фізичні   рівняння. У цю групу входять формули закону Гука або в прямій формі:

(2.5)

або у зворотній формі:

(2.6)

Маючи ці залежності, можна приступити безпосередньо до розв’язання задач теорії пружності про напруги й деформації, що виникають у пружному ізотропному тілі під дією зовнішніх сил.

Рівняння (2.1)-(2.6) містять 15 невідомих функцій:

шість складових напруг

шість складових деформацій

три складові переміщення

Для визначення цих функцій розташовуємо 15 рівняннями: трьома диференціальними рівняннями рівноваги (2.1), шістьма геометричними співвідношеннями Коші (2.3) і шістьма формулами закону Гука (2.5) або (2.6). Таким чином, з математичної точки зору задача може бути вирішена й зводиться до інтегрування зазначених 15 рівнянь при задоволенні умов на поверхні (2.2).

Розв’язання рівнянь можна вести різними способами залежно від того, які величини прийняті за основні невідомі.

1.      Розв’язання в  переміщеннях, коли  за невідомі прийняті  три складові  переміщення 

2.  Розв’язання в напругах, коли за невідомі прийняті шість складових напруг 

3.  Розв’язання в змішаній формі, коли за невідомі прийняті деякі складові переміщень і деякі складові напруг.