1.5 Комплексный чертеж /эпюр/ точки.
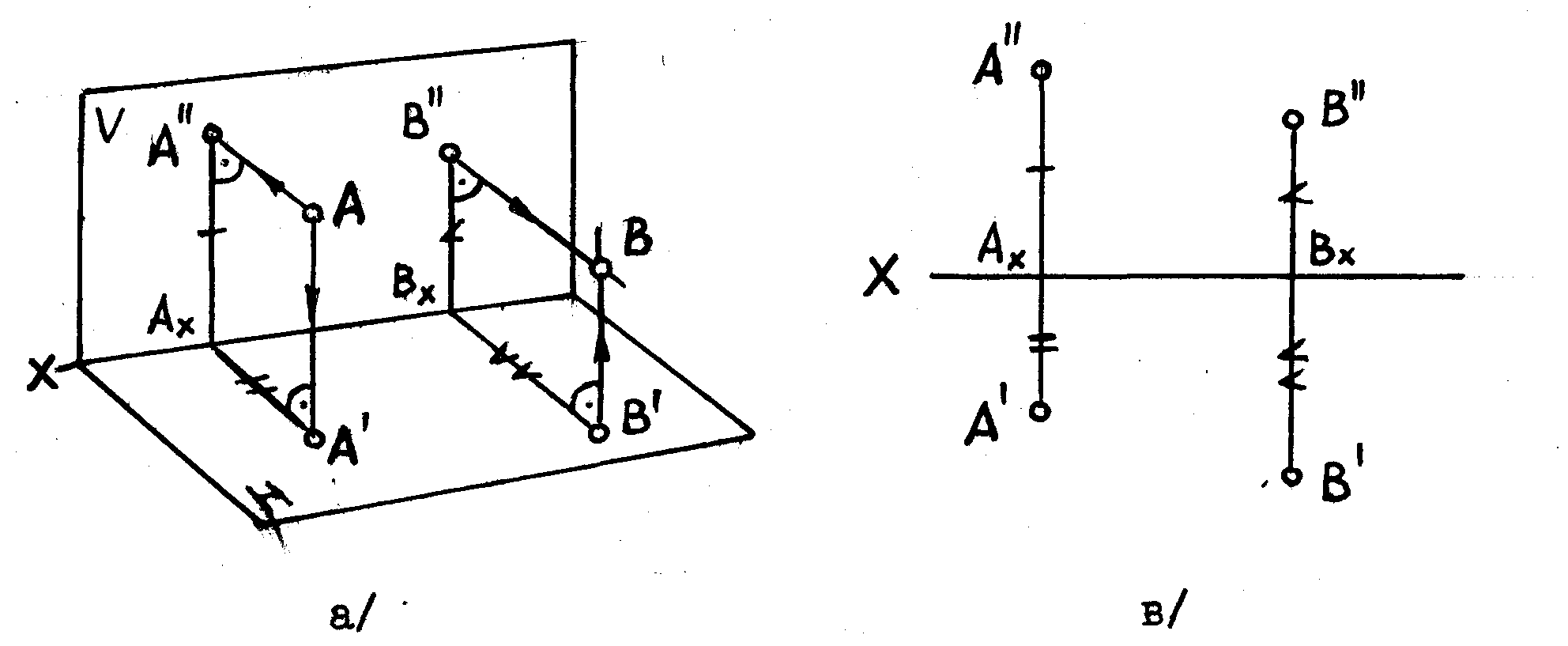
Рис 1.4.
1.6
Как видим из рис.1.4 а двухкартинный чертеж, т.е. чертеж, содержащий две плоскости проекций, обладает свойством обратимости. Имея две проекции точки – В’ и В", мы всегда сможем найти положение в пространстве самой точки В.
Одну из плоскостей - плоскость Н мы будем называть г о р и з о н т а л ь н о й п л о с к о с т ь ю п р о е к ц и й, вторую плоскость, перпендикулярную Н, плоскость V - ф р о н т а л ь н о й п л о с к о с т ь ю п р о е к ц и й.
Легко, однако, заметить существенное противоречие, возникшее между поставленной нами целью и полученными результатами.
В самом деле, наша задача состоит ведь в том, чтобы получить изображение пространственной фигуры на о д н о й плоскости /на плоскости листа бумаги/, а оказалось,что для того чтобы определить положение в пространстве простейшей геометрической фигуры - точки, т.е. сделать чертеж обратимы, мы вынуждены взять две взаимно перпендикулярные плоскости, т.е. прибегнуть к помощи пространственной, трехмерной модели.
Как же избавиться от этого противоречия? Как преодолеть • возникшее затруднение?
Наиболее удобен для этого способ совмещения плоскостей проекций. Суть этого способа состоит в следующем.
Представим себе, что наш чертеж согнут пополам под прямым углом /см.рис.1.4 а/. Одну из его половин будем считать плоскостью Н, другую - плоскостью V . После того как точка будет спроецирована на Н и V, чертеж разгибается. Тогда обе проекции точки будут находиться в одной плоскости, одна под другой и мы получим изображение, приведенное на рис.1.4 б. Это изображение называют к о м п л е к с н ы м ч е р т е ж о м или э п ю р о м М о н ж а или просто э п ю р о м.
Сообщить, что Гаспар Монж / 1746 - 1818 /, выдающийся французский ученый, математик, геометр, является создателем начертательной геометрии /1795/. Отдельные приемы и правила начертательной геометрии, в частности проекция фигур на две плоскости проекций, были известны до Монжа. Однако впервые методы начертательной геометрии были научно обобщены и последовательно изложены Г.Монжем.
Отметить, что метод Монжа в общих чертах должен быть известен слушателям из средней школы по курсу черчения.
Закономерности построения комплексного чертежа и его связь с действительной пространственной моделью двух взаимно перпен-
1.7
дикулярных плоскостей проекций должны быть усвоены студентами совершенно отчетливо.
Чтобы судить о расположении точки в пространстве и о форме изображенного предмета /это наша последующая задача/, имея их комплексный чертеж, надо непременно сопоставить о б е проекции.Только в своей совокупности они характеризуют форму и расположение предмета. Значит, чтобы понять эпюр, надо проделать некоторую мысленную работу. Некоторые склонны забывать об этом чрезвычайно важном обстоятельстве. Без твердого усвоения принципов построения и чтения комплексного чертежа нельзя понять содержание и дальнейшее изложение нашего курса.
Рассматривая комплексный чертеж /рис.1.4б/ мы должны сделать следующие выводы.
1. Две проекции точки вполне определяют положение точки в пространстве.
2. Проекции точки всегда лежат на линии связи, перпендикулярной оси проекции
Линии, соединяющие проекции точки мы будем называть линиями связи и будем изображать их сплошными тонкими линиями.
В дальнейшем, как правило, мы будем пользоваться только двумя плоскостями проекций.
Однако, как это мы увидим в дальнейшем, некоторые задачи удобно решать при использовании третьей плоскости проекций-W, которую называют профильной плоскостью проекций /рис.1.5 а/. Плоскость проекций W перпендикулярна оси проекций х, т.е. она перпендикулярна как плоскости проекций Н, так и плоскости проекций V .
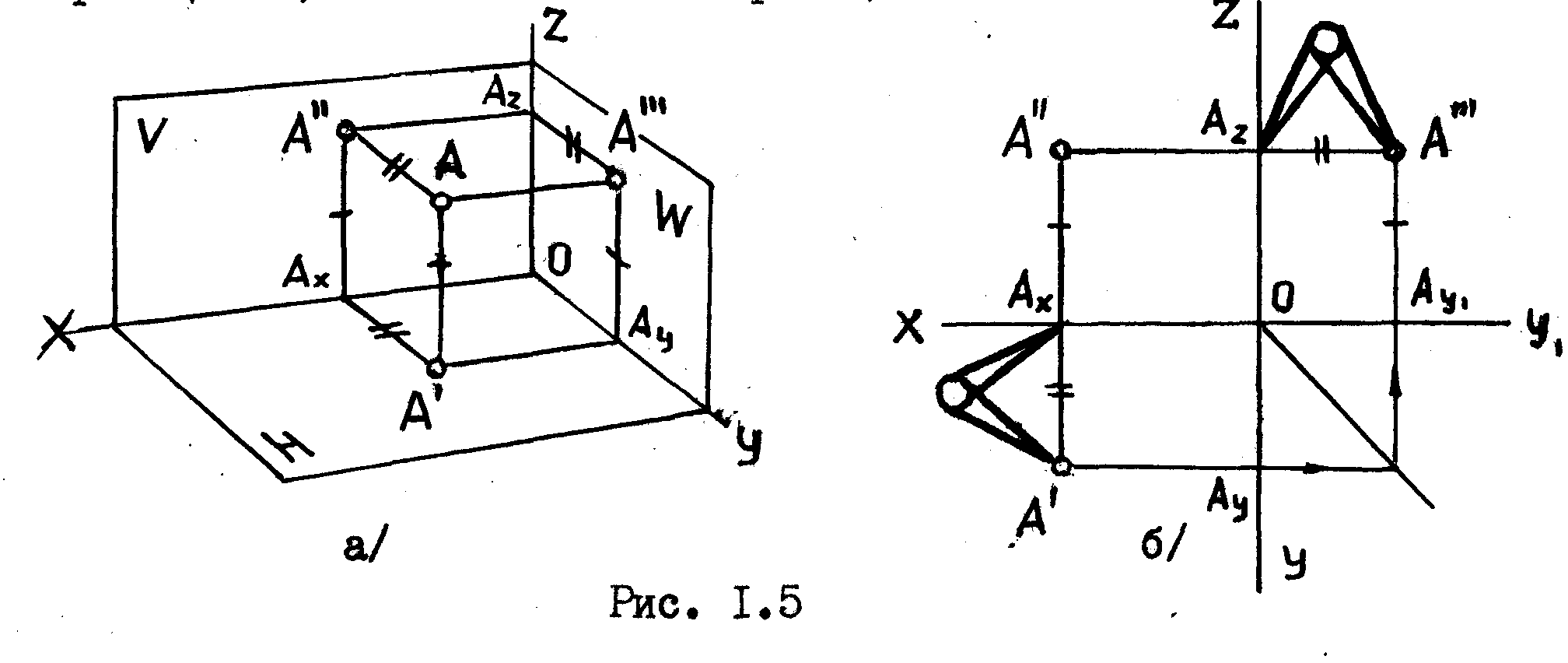
1.8
При построении комплексного чертежа все три плоскости проекций совмещаются в одну плоскость - плоскость чертежа /рис. 1.5 б /, т.е. плоскость проекций Н совмещается с плоскостью проекций V вращением около оси проекций х, а плоскость проекций V - вращением около оси проекций Z .
Рассматривая этот комплексный чертеж, сделаем следующие выводы.
1. Если заданы две проекции точки, то третья её, проекция не может быть выбрана произвольно.
2. Если линия связи А’ а" перпендикулярна оси проекций х, то линия связи А’А” всегда перпендикулярна оси проекций Z.
Примечание. При изложении параграфа 1.5 "Комплексный чертеж точки" не следует останавливаться на подробном рассмотрении всех вопросов этого раздела. Надо иметь в виду, что такие вопросы, как определение расстояний от точки до плоскостей и осей проекций, частные положения точек, будут подробно рассмотрены и изучены на первых практических занятиях.
1.6_Система обозначений.
Авторы многочисленных учебников по начертательной геометрии применяют различные системы обозначений. Мы примем систему обозначений, совпадающую с системой, принятой С.А.Фроловым, автором рекомендуемого, учебника в его первом издании.
Содержание лекции № I изложен(& в учебнике С.А.Фролова на стр. 3-9, 12-15, 21-30).
2.1