Теорема 2. Справедливы следующие соотношения:

1) = + ;

2) = –;

3) = ;

4) = .

Доказательство.

Доказательство 1) – 4) однообразно и сводится к подсчёту левой и правой частей и их сравнению. Например: z₁=a+bi, z₂=c+di. Докажем

1) = +. По определению

= a-bi ; =c-di и

= (a+c)–(bi+di),

+= (a–bi)+(c–di) = (a+c)–(bi+di).

Значит = +.

§3. Тригонометрическая форма комплексного числа.

Пусть z = a+bi , полагаем r=|z|, r — модуль комплексного числа z.

a+bi = , положим

= cos и = sin.

Пусть z0, тогда угол  определен однозначно с точностью до 2k. Если 02, то он определен однозначно. Угол  называют аргументом комплексного числа z, r и  — полярные координаты точки.

Из тригонометрии мы знаем как искать , если известно a и b.

Если r=0, то  может быть любой, то есть аргумент нуля не определён; r0, то аргумент определен с точностью до 2πk.

z = r(cos+i sin) (1)

Назовем выражение (1) тригонометрической формой комплексного числа.

Если два комплексных числа равны, то их модули равны, а их аргументы, вообще говоря, отличаются на 2k.

Теорема 1.

Пусть z₁ = r₁ (cos₁+i sin₁), z₂ = r₂ (cos₂+i sin₂). Тогда:

1. z₁z₂ = r₁r₂(cos(₁+₂)+i sin(₁+₂))

( модуль произведения комплексных чисел равен произведению модулей, а аргумент – сумме аргументов);

2)

(модуль частного комплексных чисел равен частному модулей, а аргумент – разности аргументов).

Доказательство:

Докажем 1).

z₁z₂ = r₁r₂(cos₁cos₂– sin₁sin₂+i(sin₁cos₂+cos₁sin₂)) = =r₁r₂cos(₁+₂)+i sin(₁+₂)).

Аналогично с частным.

Следствие 1.

Пусть z = r (cos+i sin), тогда z=(cos(–)+i sin(–)).

Доказательство:

z== ==(cos(–)+i sin(–)).

Следствие 2 (формула Муавра).

Пусть z = r (cos+i sin). Тогда zⁿ = rⁿ(cos(n)+i sin(n)) для любого nZ.

Доказательство:

Если n — натуральное, то формула Муавра следует из правила умножения комплексных чисел в тригонометрической форме.

Если n — отрицательное, то можно представить zⁿ = (z ^-1)^-n и применить следствие (1) и доказанную формулу Муавра для nN.

Замечание. Тригонометрическая форма комплексного числа хорошо приспособлена для выполнения действий умножения, деления, возведения в степень.

Упражнение. Интерпретировать умножение и деление в тригонометрической форме геометрически.

§4. Извлечение корня из комплексного числа.

Пусть z = a+bi.

Надо извлечь корень из z.

— ?

обозначим через z₁, то z= z.

Пусть z₁ = x+iy, тогда

(x²–y²)+2xyi = a+bi,

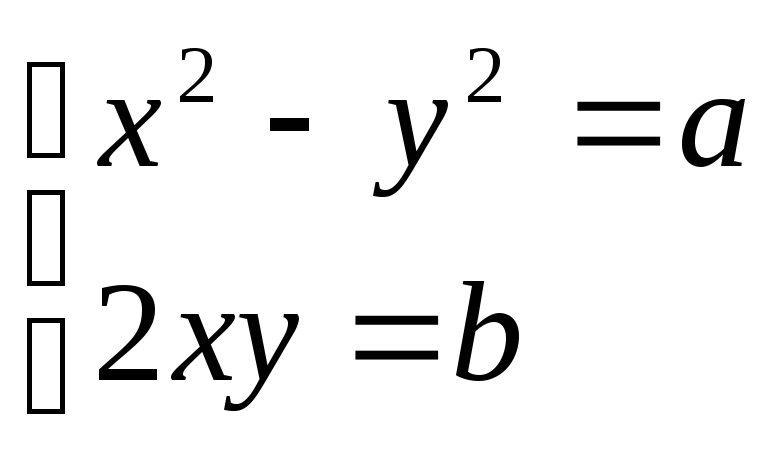
Решив эту систему, мы найдем подходящие значения z₁.

Если так действовать и для извлечения корней более высокой степени, то придётся уметь решать уравнения соответствующих степеней.

Для извлечения корня из комплексного числа хорошо приспособлена тригонометрическая форма комплексного числа.

Пусть z = r(cos+i sin), надо найти = z₁, положим

z₁=ρ (cos+i sin), z==ρⁿ(cos(n)+i sin(n), r = ρⁿ  ρ = ,  = n+2k  = .

Получим

= (cos+i sin) (1),

где k — любое целое число, то есть корень n–той степени из произвольного комплексного числа z всегда существует и его можно посчитать по формуле (1), причем формула (1) даёт все корни, если k пробегает множество целых чисел (достаточно ограничиться k = 0,…, n–1 )

Если возьмем k – любое, то мы можем разделить его с остатком на n:

k = nq+s ; 0sn–1

.

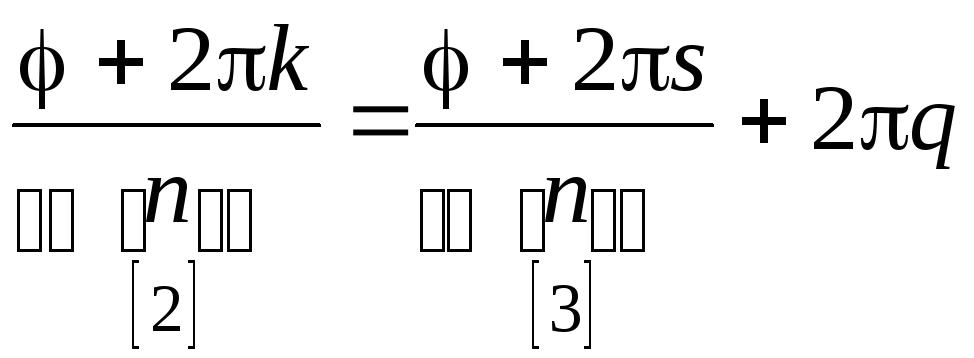Углы [2] и [3] отличаются на кратное 2, и поэтому косинусы и синусы от них совпадают, следовательно формула (1) при угле [2] и при угле [3] даёт одинаковое значение.

Если брать k от 0 до n–1 , то мы получим все значения. Нетрудно заметить, что все эти значения разные (смотри геометрическую интерпретацию).

Теорема 4.

Извлечение корня степени n из комплексного числа всегда возможно, и даёт n различных значений, получающихся по формуле (1).

Теорема нами доказана ранее.

Замечание (геометрическая интерпретация).

Все значения расположены на окружности радиуса с центром в начале координат и делят окружность на n равных частей: