Теорема 2. Нод определен однозначно.

◄Пусть d₁ и d₂ — наибольшие общие делители многочленов .

Тогда d₁ делит ,то есть d₁ │ , отсюда следует, что d₁ / d₂ ( по 3 свойству НОД). Аналогично d₁ │ d₂ ,значит можно записать d₁₌аd₂ . А так как d₁ и d₂ со старшим коэффициентом 1,то в качестве а можно взять только единицу (а=1). Значит d₁=d₂ ,т.е. НОД определен однозначно.►

Лемма 2. Пусть f(x)=g(x)q(x)+r(x).Тогда наибольший общий делитель f и g равен наибольшему общему делителю g и r, т.е.: ( f, g )=( g, r ).

◄Доказательство теоремы следует из определения. Пусть ( f, g ) = d₁ , ( g, r) = d₂ .Тогда:

d₁ │ f d₂ │ g

 d₁│ r  d₁ │ d₂ и d₂ │ d₁  d₂ │ f 

d₁ │ g d₂│ r

А значит: d₁= d₂.►

Теорема 3 (об отыскании нод для двух многочленов).

Пусть f(x), g(x)P[x], g(x)0. Тогда НОД многочленов f и g равен последнему, отличному от нуля, остатку в алгоритме Евклида для этих многочленов, взятому со старшим коэффициентом — единица. Если g | f, то НОД ( f, g ) равен .

◄Если g / f ,то последнее утверждение в формулировке теоремы очевидно.

Применяя Лемму 2 к системе равенство (4) предыдущего параграфа, получим ,что

( f, g )=(g,r)=…=( r_k ; r_k-1 )= ;

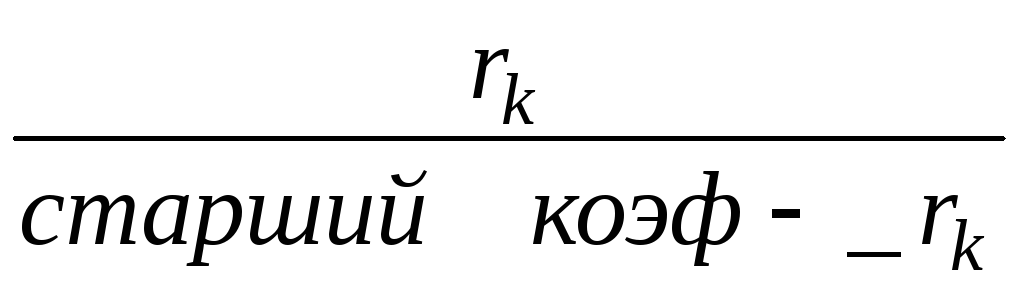P.S. f=gq+r

g=rq₁+r₁

…………. система (4)

r_k-2=r_k-1+r_k

r_{k-1 =}r_kq_k+1+0.►

Замечание:

В теореме 3 содержится алгоритм практического отыскания НОД:

• Ищем последний отличный от нуля остаток в алгоритме Евклида.

• Делаем его со старшим коэффициентом единица ,это и будет НОД.

Теорема 4. (f_{1,……….,}f_k)=((f_1,……..,f_k-1) , f_k ), k≥2.

Эта теорема указывает путь, как процесс нахождения НОД для нескольких многочленов можно свести к нахождению НОД двух многочленов.

◄Доказательство следует из определения НОД.

Критерий взаимной простоты многочленов.►

Определение. Многочлены f_{1,……….,}f_k называются взаимно простыми, если их НОД равен единице.

Теорема 5 (критерий взаимной простоты).

Многочлены (f_{1,……….,} f_k ) взаимно простоты тогда и только тогда, когда u_1,……,u_k P[x], такие что единица представляется в виде f₁u₁ +……+f_ku_k.

◄ Имеем f_{1,……….,}f_k взаимно простые, то u_1,……,u_k P[x], такие что f₁u₁ +……+f_ku_k=1. Это следует из основного свойства НОД.

 Пусть d(x)=( f_{1,……….,}f_k ). Значит d(x) | 1  d(x)=1 и значит многочлены взаимно простые.►

§ 4. Наименьшее общее кратное многочленов (нок).

Определение. Пусть f₁(x),……,f_k (x)  P[x], f_i0, f_i .Многочлен h(x) называют наименьшим общим кратным многочленов f₁(x),……,f_k (x), если :

1) f_i (x) | h(x) , т.е. h(x)-общее кратное многочленов;

2. g(x), являющегося общим кратным, т.е. f_i | g , i, h(x) | g(x). Обозначают НОК таким образом : [f₁(x),……,f_k (x)] = НОК (f_{1,……….,}f_k).

Свойства НОК:

1)[f₁,f₂] = — это дает правило вычисления НОК для двух многочленов;

2) [f₁(x),……,f_k (x)] = [f₁(x),…f_k-1] ,f_k (x)] — это свойство сводит вычисление НОК для k многочленов к вычислению НОК для двух многочленов;

3),

,

[f , g]=, где , i=1,…..,s.

Всех этих свойств достаточно, чтобы находить НОК для нескольких многочленов.

Упражнение. Однозначен ли НОК (с точностью до постоянного множителя) ?

Докажем свойство 1):

◄Обозначим [f₁,f₂] через m₁ , через m_{2 , , .}

==   .

Если докажем, что ,т.е. m₁ и m₂ могут отличаться на постоянный множитель, то m₂ будет годиться в качестве НОК.►

Упражнение. Доказать, что .

Докажем свойство 3):

◄

[f,g]= ,

то , где .►