1.10. Сила Лоренца

Експериментально досліджуючи дію магнітних полів на катодне випромінювання, виявили, що магнітне поле діє на рухомі електричні заряди. У цьому можна впевнитись на дослідах з електронними пучками. За допомогою електронно-променевої трубки в центрі екрана одержують світну точку О, яка виникає внаслідок бомбардувань флуоресціюючого шару розігнаним до великих швидкостей сфокусованим пучком електронів. Якщо ж трубку вмістити в сильне магнітне поле, то траєкторія електронів викривляється в площині, перпендикулярній до площини рисунка. Відповідно до цього зміщується світна пляма на екрані. На рис. 1.19 зображено нові положення плями (чорні кола),

Рис. 1.19 коли швидкість електронів напрямлена з-за рисунка.

Дослід показує, що в зовнішньому магнітному полі електрони відхиляються в напрямку, перпендикулярному до вектора індукції і швидкості руху зарядів. Отже на електрон, що рухається в магнітному полі, діє сила, яка напрямлена в той самий бік, що й векторний добуток .

Спостереження над рухом у магнітному полі позитивних і негативних іонів показали, що на них теж діють сили, напрямлені перпендикулярно до векторів і . Було встановлено, що для позитивно заряджених частинок напрямок сили збігається з напрямком вектора , а для негативно заряджених частинок – з напрямком вектора (рис. 1.20).

Д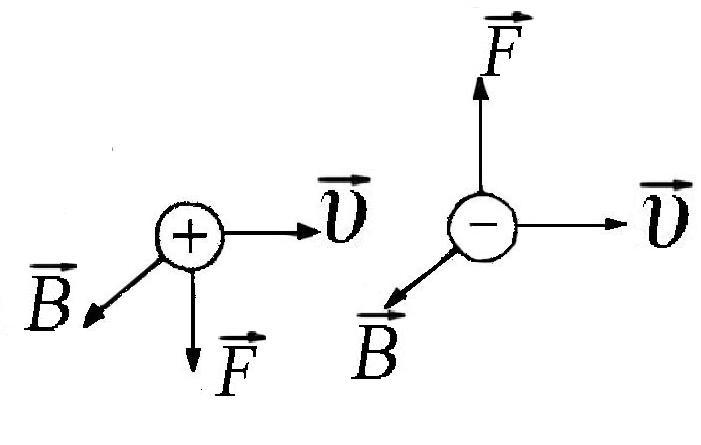ію магнітного поля на провідник із струмом можна уявити як дію магнітного поля на заряджені частинки, що створюють струм, з передачею цієї дії провіднику. Опираючись на закон Ампера, знайдемо вираз для сили, що діє на електричний заряд, який рухається в магнітному полі. За законом Ампера (1.30) на елемент провідника з струмом , який перебуває в

Рис. 1.20 магнітному полі, діє сила , що дорівнює

.

Якщо струм у провіднику зумовлений рухом частинок, заряд яких дорівнює , то

,

де - кількість частинок в об’ємі провідника довжиною , а - швидкість їхнього упорядкованого руху. Сила , що визначається співвідношенням (1.30), діє на всі заряджені частинки. Очевидно, що сила, з якою магнітне поле діє на одну рухому частинку, дорівнює

. (1.31)

До такого ж висновку дійшов нідерландський фізик Х. Лоренц (Lorentz). Тому силу, що визначається формулою (1.31), називають силою Лоренца ().

Зважаючи на вище наведені результати дослідів, слід зауважити, що в формулі (1.31) необхідно враховувати знак заряду.

Числове значення сили Лоренца дорівнює

, (1.32)

де - кут між векторами і .

В електричному полі напруженістю на заряд , незалежно від того, рухається він чи перебуває у стані спокою, діє сила . Як показують досліди, електричне і магнітне поля діють незалежно. Тому в довільному електромагнітному полі або у разі сумісної дії електричного і магнітного полів результуюча сила , тобто

. (1.33)

Вираз (1.33) називають формулою Лоренца, а силу, що визначається цією формулою, іноді називають силою Лоренца (див. [5]).