1.9. Закон Ампера

У підрозділі 1.1 йшлося про те, що провідники зі струмом створюють навколо себе магнітне поле і діють на постійні магніти, які містяться поблизу них. Як свідчать досліди, магнітне поле у свою чергу діє на провідник із струмом.

Дію магнітного поля на провідник із струмом вивчали Х.Ерстед і А.Ампер. Ампер докладно дослідив це явище і дійшов висновку, що сила , яка діє на прямолінійний провідник із струмом, що перебуває в однорідному магнітному полі, прямо пропорційна силі струму в провіднику, його довжині , магнітній індукції і синусу кута між напрямком струму в провіднику і вектором :

. (1.28)

Закон Ампера (1.28) можна узагальнити на випадок неоднорідного магнітного поля і провідника довільної форми. Справді, нескінченно малий елемент провідника будь-якої форми можна вважати прямолінійним, а магнітне поле в області, яку займає елемент , можна вважати однорідним. Тому в загальному випадку закон Ампера має вигляд

, (1.29)

де - сила, що діє на елемент провідника довжиною , - кут між вектором (проведеним в напрямку струму у цій ділянці провідника) і вектором . Коефіцієнт пропорційності у формулах (1.28) і (1.29) залежить тільки від вибору одиниць вимірювання величин, що входять у ці формули. У Міжнародній системі одиниць . Тому надалі коефіцієнт в законі Ампера опускатимемо.

Закон Ампера, записаний у вигляді (1.29), не вказує напрямок сили і тому не визначає її повністю. Як показали досліди (див. рис.1.16), напрямок сили можна знайти за правилом лівої руки (рис. 1.17): якщо долоню лівої руки поставити так, щоб в неї входили лінії магнітної індукції, а чотири витягнутих пальці спрямувати в напрямку електричного струму у провіднику, то відставлений великий палець покаже напрямок сили, що діє на провідник з боку поля. Якщо елемент провідника із струмом не перпендикулярний до напрямку магнітного поля, то у долоню мають входити перпендикулярні до провідника складові векторів . Взагалі краще скористатись універсальним правилом – правилом векторного добутку (див. рис. 1.18).

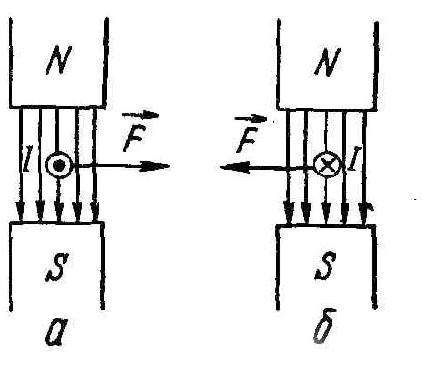
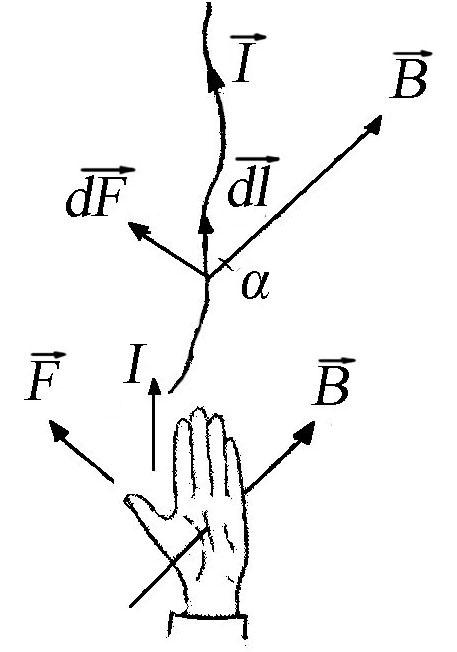
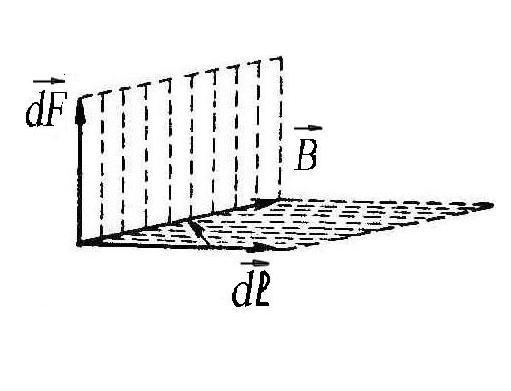
Рис. 1.16 Рис. 1.17 Рис. 1.18

Оскільки модуль векторного добутку дорівнює добутку модулів векторів на синус кута між ними , то можна записати закон Ампе-

ра у векторній формі.

. (1.30)

Якщо прийняти, що в дослідах Ампера з нескінченними прямими паралельними провідниками із струмами та струм створює магнітне поле, індукція якого (див. (1.13)), а кожен елемент провідника із струмом знаходиться в цьому полі, то, згідно з законом Ампера, сила, з якою поле діє на одиницю довжини другого провідника , що узгоджується формулою (1.1).

Сила, що діє на точковий заряд , вміщений в електростатичне поле з напруженістю , збігається за величиною і напрямком з вектором , тобто напрямлена по дотичній до силової лінії електростатичного поля. Сили цього поля є центральними. А сили магнітної взаємодії, як видно із закону Ампера (1.30), не є центральними. Вони завжди напрямлені перпендикулярно до ліній магнітної індукції. Як показує дослід, закон Ампера виконується як для нерухомих, так і для рухомих провідників із струмом в магнітному полі. Це дало можливість створити електричні двигуни.