Size(c)
ans =
2 2 1 2
Ndims(c)
ans =
4
Индексация
Многие концепции, используемые в двумерном случае, распространяются также на много-мерные массивы. Для выделения (обращения) к какому-либо одному элементу многомерного массива следует воспользоваться целочисленной индексацией. Каждый индекс указывает на соответствующую размерность: первый индекс на размерность строк, второй индекс на раз-мерность столбцов, третий на первую размерность страниц и так далее. Рассмотрим массив случайных целых чисел nddata размера 10х5х3:
nddata = fix (8*randn (10, 5, 3));
Для обращения к элементу (3,2) на странице 2 массива nddata нужно записать nddata(3,2,2).
Вы можете также использовать векторы как массив индексов. В этом случае каждый элемент вектора должен быть допустимым индексом, то есть должен быть в пределах границ, опре-деленных для размерностей массива. Так, для обращения к элементам (2,1), (2,3), и (2,4) на странице 3 массива nddata, можно записать
Nddata (2, [1 3 4], 3). Оператор двоеточия и индексирование многомерных массивов.
Стандартная индексация MATLAB-а при помощи оператора двоеточия (colon) применима и в случае многомерных массивов. Например, для выбора всего третьего столбца страницы 2 массива nddata используется запись nddata(:, 3, 2). Оператор двоеточия также полезен и для выделения определенных подмножеств данных. Так, ввод nddata(2:3,2:3,1) дает массив (мат-рицу) размера 2х2, который является подмножеством данных на странице 1 массива nddata. Эта матрица состоит из данных второй и третьей строки и сторого и третьего столбца первой стриницы многомерного массива. Оператор двоеточия может использоваться для индексации с обеих сторон записи. Например, для создания массива нулей размера 4х4 записываем:
C = zeros (4,4)
Теперь, чтобы присвоить значения подмножества 2х2 массива nddata четырем элементам в центре массива С запишем
C(2:3,2:3) = nddata (2:3,1:2,2)
Устранение неопределенностей в многомерной индексации
Некоторые выражения, такие как
A(:, :, 2) = 1:10
Являются неоднозначными, поскольку они не обеспечивают достаточного объема информа-ции относительно структуры размерности, в которую вводятся данные. В представленном выше случае, делается попытка задать одномерный вектор в двумерном объекте. В таких ситуациях MATLAB выдает сообщение об ошибке. Для устранения неопреденности, нужно убедиться, что обеспечена достаточная информация о месе записи данных, и что как данные так и место назначения имеют одинаковую форму. Например,
A(1,:,2) = 1:10.
Изменение формы (Reshaping)
Если вы не меняете форму или размер, массивы в системе MATLAB сохраняют размернос-ти, заданные при их создании. Вы можете изменить размер массива путем добавления или удаления элементов. Вы можете также изменить форму массива изменяя размерности строк, столбцов и страниц, при условии сохранения тех же элементов. Функция reshape выполняет указанную операцию. Для многомерных массивов эта функция имеет вид
B = reshape (A, [s1 s2 s3 ...] )
где s1, s2, и так далее характеризуют желаемый размер для каждой размерности преобразо-ванной матрицы. Отметим, что преобразованный массив должен иметь то же число элемен-тов, что и исходный массив (иными словами, произведение размеров массивов должно быть неизменным).
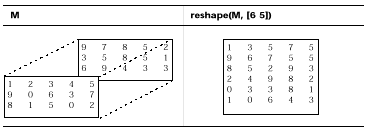
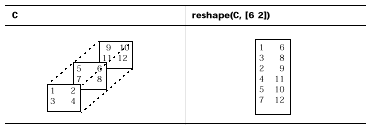
Функция reshape «действует» вдоль столбцов. Она создает преобразованную матрицу путем взятия последовательных элементов вдоль каждого столбца исходной матрицы.
Ниже в качестве примеров приведены несколько примеров массивов, которые могут быть получены из массива nddata (обратите внимание на размерности).
B = reshape(nddata,[6 25])
C = reshape(nddata,[5 3 10])
D = reshape(nddata,[5 3 2 5])
Удаление единичных размерностей.
Система MATLAB создает единичные размерности, когда вы задаете их при создании или преобразовании массива, или же в результате вычислений приводящих к появлению указан-ных размерностей.
B = repmat (5, [2 3 1 4] ) ;
size(B)
ans =
2 3 1 4
Функция squeeze удаляет единичные размерности из массива.
C = squeeze(B);
size(C)
ans =
2 3 4
Функция squeeze не оказывает воздействия на двумерные массивы – векторы-строки оста-ются строками.
Вычисления с многомерными массивами
Многие вычислительные и математические функции MATLAB-а принимают в качестве аргументов многомерные массивы. Эти функции действуют на определенные размерности многомерных массивов, в частности, на отдельные элементы, векторы или матрицы.
Действия над векторами
Функции которые действуют над векторами, такие как sum, mean, и т.д., по умолчанию обы-чно действуют вдоль первой неединичной размерности многомерного массива. Многие из этих функций дают возможность задать размерность вдоль которой они действуют. Однако, есть и исключения. Например, функция cross, которая определяет векторное произведение двух векторов, действует вдоль первой неединичной размерности, имеющей размер 3.
Внимание! Во многих случаях эти функции имеют другие ограничения на входные аргумен-ты – например, некоторые функции, допускающие многомерные входные массивы, требуют чтобы массивы имели одинаковый размер.