
- •1. Пояснительная записка
- •3. Краткий теоретический курс дисциплины «Маркетинговое поведение покупателей в торговом менеджменте»
- •1. Российское предпринимательство с позиций теории мотивации поведения потребителей
- •1.1 Зарождение и развитие российского предпринимательства и последовавшая реакция потребителей на это развитие.
- •1.2 Социальное расслоение в российском обществе и российское предпринимательство.
- •1.4 Теория мотивации процессов в коммуникативной политике системы маркетинга применительно к российскому предпринимательству.
- •2. Трансформация современных научных теорий маркетинга, поведения потребителей и мотивации их поведения с позиции пространственно-временной аксиоматики.
- •2.1 Построение пространственно-временных аксиоматических описаний маркетинговых теорий.
- •Оснований ядра
- •2.2 Современные теории поведения потребителей в пространственно-временном аксиоматическом представлении.
- •2.3 Современные теории мотивации поведения потребителей в пространственно-временном аксиоматическом представлении (с учётом персонального и социального влияний).
- •2.4 Аксиоматическое построение теорий влияния ситуации и среды на мотивацию поведения потребителя.
- •Координатная система информационного пространства
- •Параметр влияния ситуации при коммуникации
- •Параметр, характеризующий динамику регулирования взаимодействия соотношений между характеристиками осей и
- •Параметр наличия коммуникативности семейных навыков, способствующих регулированию взаимодействия между сплочённостью семьи и её способности к адаптации
- •2.6 Аксиоматическая теория пространственно-временного описания мотивации процессов в коммуникативной политике системы маркетинга.
- •Параметр управления процессом мотивации, включая планирование, организацию и комплексный анализ мотивационного уровня, образующие совместно обратную связь
- •Обоснование научного факта мотивации поведения потребителей в «пространстве – времени».
- •Моделирование эксперимента для выделения характеристики одного координатного измерения мотивационного пространства.
- •Условия и особенности проведения эксперимента.
- •3.4 Обработка данных и проверка статистической гипотезы на соответствие нормальному закону распределения полученных массивов данных.
- •Задание числа значений n
- •3.5 Условия проведения эксперимента и выявление признаков стационарности.
- •4. Построение аксиоматической теории мотивационного поведения потребителей применительно к российскому предпринимательству
- •4.2 Распределение потребителей по мотивируемым ценам на товар
- •4.3 Средние и наивероятнейшие цены, мотивируемые потребителями
- •4.4 Относительная цена мотивации и стандартное распределение мотивационного поведения потребителей.
- •4.5 Техника статистических вычислений плотности распределения мотивируемых цен и определение параметра распределения .
- •4.6 Применение стандартного распределения цен мотивации для решения практических задач.
4.5 Техника статистических вычислений плотности распределения мотивируемых цен и определение параметра распределения .
Исследования,
представленные в предыдущем параграфе,
указывают на существенную значимость
для вычислений параметра распределения
![]() ,
который подлежит определению. Для этого
необходим статистический сбор данных
с последующей их обработкой. При этом
функция
,
который подлежит определению. Для этого
необходим статистический сбор данных
с последующей их обработкой. При этом
функция
![]() ,
используемая для аппроксимации,
определяется согласно выражению, где
независимые переменные определяются
путём статистического опроса потребителей,
то есть
,
используемая для аппроксимации,
определяется согласно выражению, где
независимые переменные определяются
путём статистического опроса потребителей,
то есть
![]() ,
(4-55)
,
(4-55)
где
![]() - общее количество
потребителей в принятом нами единице
объёма маркетингового пространства
мотивации;
- общее количество
потребителей в принятом нами единице
объёма маркетингового пространства
мотивации;
![]() - выбранный
диапазон изменения мотивационной цены,
в пределах которого мысленно назначенная
цена
- выбранный
диапазон изменения мотивационной цены,
в пределах которого мысленно назначенная
цена
![]() соответствует количеству потребителей
соответствует количеству потребителей
![]() .
.
В результате
выборочного опроса статистически
представительного числа потребителей
![]() и выделения из них количества
и выделения из них количества
![]() ,
назначивших цену
,
назначивших цену
![]() ,
представляется возможным вычислить по
формуле (4-55) значения функции распределения
,
представляется возможным вычислить по
формуле (4-55) значения функции распределения
![]() ,
соответствующей мотивируемой потребителями
цене
,
соответствующей мотивируемой потребителями
цене
![]() .
При этом, статистическая представительность
числа потребителей в единице объёма
пространства может быть достигнута
путём выбора представительного числа
из таблицы достаточно больших чисел
с заранее заданной ошибкой. [243].
.
При этом, статистическая представительность
числа потребителей в единице объёма
пространства может быть достигнута
путём выбора представительного числа
из таблицы достаточно больших чисел
с заранее заданной ошибкой. [243].
Тогда полученные экспериментальные данные вида:
Таблица 4.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
позволяют далее аппроксимировать эти данные методом наименьших квадратов при помощи функции:
![]() ,
(4-56)
,
(4-56)
где
![]() и
и
![]() соответствуют значениям таблицы 4.2.
соответствуют значениям таблицы 4.2.
Аппроксимируя
данные таблицы 4.2 методом наименьших
квадратов с использованием (4-56), можно
получить оптимальные коэффициент для
![]() в (4-56) с точки зрения минимума суммарного
квадратичного приближения параметров
функции (4-56) к статистическим данным.
Это позволит далее использовать
оптимальный параметр
в (4-56) с точки зрения минимума суммарного
квадратичного приближения параметров
функции (4-56) к статистическим данным.
Это позволит далее использовать
оптимальный параметр
![]() для вычисления рассматриваемых средней,
наивероятнейшей и относительной цен,
связанных с их мотивацией потребителями.
Вывод соотношений, связанных с числовым
расчётом оптимального коэффициента
для вычисления рассматриваемых средней,
наивероятнейшей и относительной цен,
связанных с их мотивацией потребителями.
Вывод соотношений, связанных с числовым
расчётом оптимального коэффициента
![]() для аппроксимирующей теоретической
регрессии в соответствии с (4-56),
приведен ниже.
для аппроксимирующей теоретической
регрессии в соответствии с (4-56),
приведен ниже.
Функция
![]() ,
используемая при аппроксимации,
определяется согласно выражению, где
независимые переменные определяются
путём статистического опроса потребителей,
то есть
,
используемая при аппроксимации,
определяется согласно выражению, где
независимые переменные определяются
путём статистического опроса потребителей,
то есть
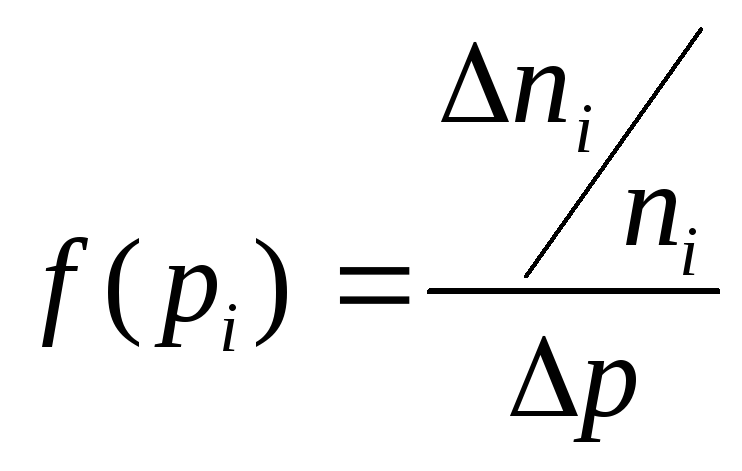 ,
(4-57)
,
(4-57)
где
![]() - общее количество
потребителей в принятом нами единице
объёма маркетингового пространства
мотивации (эта величина выбирается
таким образом, чтобы путём умножения
её на объём маркетингового пространства
получить общее число потребителей
- общее количество
потребителей в принятом нами единице
объёма маркетингового пространства
мотивации (эта величина выбирается
таким образом, чтобы путём умножения
её на объём маркетингового пространства
получить общее число потребителей
![]() ;
;
![]() - выбранный
диапазон изменения мотивационной цены,
в пределах которого мысленно назначенная
цена
- выбранный
диапазон изменения мотивационной цены,
в пределах которого мысленно назначенная
цена
![]() соответствует количеству потребителей
соответствует количеству потребителей
![]() .
.
В результате
выборочного опроса статистически
представительного числа потребителей
![]() и выделения из них количества
и выделения из них количества
![]() ,
назначивших цену
,
назначивших цену
![]() ,
представляется возможным вычислить по
формуле (4-57) значения функции распределения
,
представляется возможным вычислить по
формуле (4-57) значения функции распределения
![]() ,
соответствующей мотивируемой потребителями
цене
,
соответствующей мотивируемой потребителями
цене
![]() .
При этом, статистическая представительность
числа потребителей в единице объёма
пространства может быть достигнута
путём выбора представительного числа
из таблицы достаточно больших чисел
с заранее заданной ошибкой [243].
.
При этом, статистическая представительность
числа потребителей в единице объёма
пространства может быть достигнута
путём выбора представительного числа
из таблицы достаточно больших чисел
с заранее заданной ошибкой [243].
Тогда полученные экспериментальные данные вида:
Таблица 4.3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Позволяют далее аппроксимировать эти данные методом наименьших квадратов при помощи функции:
![]() ,
(4-58)
,
(4-58)
где
![]() и
и
![]() соответствуют значениям таблицы 4.3.
соответствуют значениям таблицы 4.3.
Аппроксимируя
данные таблицы 4.3 с использованием
(4-57), можно получить оптимальные
коэффициенты для (4-58) с точки зрения
минимума суммарного квадратичного
приближения параметров функции (4-58) к
статистическим данным. Это позволит
далее оптимизировать полученные
коэффициенты таким образом, чтобы
получить оптимальный параметр
![]() ,
необходимый для вычисления рассматриваемых
средней, наивероятнейшей и относительной
цен, связанных с их мотивацией
потребителями.
,
необходимый для вычисления рассматриваемых
средней, наивероятнейшей и относительной
цен, связанных с их мотивацией
потребителями.
Для указанного сделаем в (4-58) замену переменной:
![]() (4-59)
(4-59)
и приведём (4-58) к линейному виду путём логарифмирования [56, 25]:
![]() ,
(4-60)
,
(4-60)
где
![]()
Оптимизация
методом наименьших квадратов сводится
к образованию функции
![]() как суммы разностей квадратов между
статистическим или экспериментальными
значениями
как суммы разностей квадратов между
статистическим или экспериментальными
значениями
![]() в соответствии с табл. 4.3 и теоретическими
значениями в соответствии с (4-60) [56, 68,
89, 243], то есть
в соответствии с табл. 4.3 и теоретическими
значениями в соответствии с (4-60) [56, 68,
89, 243], то есть
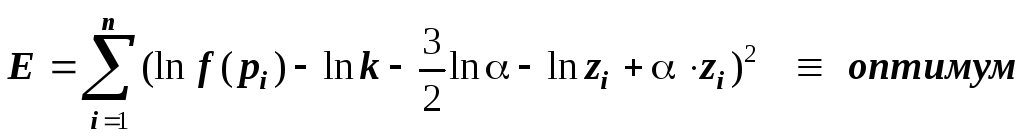 .
(4-61)
.
(4-61)
Тогда оптимум определяет условие
![]() (4-62)
(4-62)
и, следуя (4-61), имеем
![]() .
(4-63)
.
(4-63)
После преобразования (4-63) получаем уравнение
![]() ,
(4-64)
,
(4-64)
где
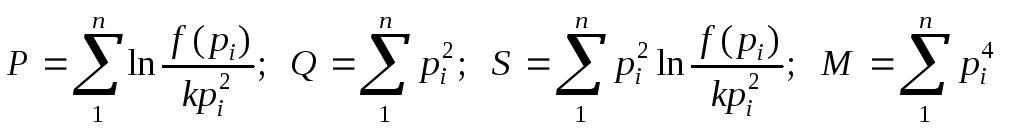 ,
(4-65)
,
(4-65)
которое
решается относительно
![]() известными численными методами [56, 243,
305] (см. Главу 5).
известными численными методами [56, 243,
305] (см. Главу 5).
Полученный
параметр
![]() позволяет получить среднюю и
наивероятнейшую цены мотивации; при
этом параметр
позволяет получить среднюю и
наивероятнейшую цены мотивации; при
этом параметр
![]() можно рассчитать известными статистическими
методами с использованием приведенных
методологических рекомендаций.
можно рассчитать известными статистическими
методами с использованием приведенных
методологических рекомендаций.
