Розділ: «Інтеграл» Лекція

Тема: Визначений інтеграл. Формула Ньютона - Лейбниця.

Ціль: Розглянути поняття визначеного інтеграла, його геометричний зміст, придбати необхідні навички при обчисленні визначених інтегралів за допомогою формули Ньютона - Лейбниця

План: 1. Поняття визначеного інтеграла

2. Геометричний зміст певного інтеграла

3. Властивості визначеного інтеграла.

4. Формула Ньютона - Лейбниця

Поняття визначеного інтеграла.

Його геометричний і економічний зміст.

Властивості визначеного інтеграла

Визначення визначеного інтеграла. Нехай функція задана на відрізку [а, b]. Розіб'ємо відрізок [а, b] на п довільних частин точками

.

Точки, що розділяють відрізок [а, b] на часткові відрізки довжиною , називаються точками розбивки. Усередині кожного часткового відрізка виберемо довільну точку . Складемо суму добутків

,

називану інтегральною сумою для функції на відрізку [а, b]. Геометричний зміст величини  показаний на мал. 1. Це сума площ прямокутників з підставами й висотами .

При цьому числа a і b називаються відповідно нижньою й верхньою межами, вираження – подінтегральним вираженням, – подінтегральною функцією.

Визначений інтеграл чисельно дорівнює площі криволінійної трапеції, обмеженої вертикальними прямими при , віссю Ох і графіком ненегативної й безперервної функції . У цьому складається його геометричний зміст.

Якщо припустити, що – продуктивність праці в момент t, то буде чисельно дорівнює об'єму зробленої продукції за проміжок , тобто визначеному інтегралу можна додати економічний зміст.

у В Мi mi А О х0=а хi хi+1 b= хn х Рис. 1

Межа інтегральної суми при прагненні до нуля, що не залежить від способу вибору точок і точок , називається визначеним інтегралом від функції на [а, b] і позначається

Визначений інтеграл володіє рядом властивостей, аналогічних властивостям невизначеного інтеграла:

1) постійний множник можна виносити за знак інтеграла;

2) інтеграл від алгебраїчної суми функцій дорівнює такій же сумі інтегралів від цих функцій (властивість лінійності).

Крім того, визначеному інтегралу властиві властивості, що не мають аналогів у теорії невизначених інтегралів:

3) інтеграл від постійної величини дорівнює цієї постійної, помноженої на довжину відрізка інтегрування

;

4) при зміні місцями меж інтегрування інтеграл змінює лише знак

;

5) інтеграл з однаковими межами інтегрування дорівнює нулю

;

6) для будь-яких чисел а, b і c має місце рівність

.

Доказу вищевказаних властивостей будуються на геометричному змісті певного інтеграла.

Важливе значення мають властивості, називані оцінками визначених інтегралів:

7) якщо всюди на відрізку , те й , тобто нерівності між функціями можна інтегрувати;

8) інтеграл від знакосталой функції на відрізку є число такого ж знака, що й функція: , якщо й , якщо ;

9) абсолютна величина інтеграла не перевершує інтеграла від абсолютної величини подінтегральної функції: ;

10) якщо М и т – відповідно максимум і мінімум функції на відрізку , те ;

11) на відрізку інтегрування найдеться принаймні одна така точка , що визначений інтеграл від безперервної функції буде дорівнює її значенню в цій точці, помноженому на довжину відрізка інтегрування (теорема про середній): . Число називається середнім значенням функції на відрізку . Геометрично теорему про середній можна витлумачити в такий спосіб: серед ординат криволінійної трапеції найдеться така, що, прийнявши її за висоту прямокутника, побудованого на тім же підставі, що й трапеція, одержимо прямокутник, рівновеликий цієї криволінійної трапеції.

Всі вищенаведені нерівності застосовуються для оцінки значення (необчисленого) визначеного інтеграла.

Визначений інтеграл як функція верхньої межі. Формула Ньютона-Лейбниця

Якщо функція інтегрувальна на відрізку , то вона інтегрувальна й на будь-якому відрізку, що втримується в ньому, і, отже, для кожного існує інтеграл . Щоб не змішувати позначення верхньої межі й змінної інтегрування, будемо записувати його у вигляді . Такий інтеграл називається інтегралом зі змінною верхньою межею.

Існує теорема, відповідно до якої інтеграл зі змінною верхньою межею є первісною для безперервної подінтегральної функції, тобто

, де .

Доводиться ця теорема за допомогою визначення похідної й теореми про середній. За допомогою останньої теореми виводиться основна формула інтегрального вирахування – формула Ньютона-Лейбниця

,

де – первісна для .

Різницю часто записують у вигляді , і формула Ньютона-Лейбниця в цьому випадку приймає вид .

Відповідно до формули Ньютона-Лейбниця визначений інтеграл дорівнює приросту первісної від подінтегральної функції на відрізку інтегрування.

Формула Ньютона-Лейбниця встановлює зв'язок між визначеним інтегралом і невизначеним інтегралом (первісної), що робить виправданим уживання знака інтеграла в обох випадках. Помітимо, що незважаючи на подібність у позначеннях і термінології, визначений і невизначений інтеграли – істотно різні поняття: невизначений інтеграл являє собою сімейство функцій, тоді як визначений інтеграл – є число.

Для визначеного інтеграла формула інтегрування вроздріб приймає наступний вид

,

а заміна змінної в визначеному інтегралі виробляється відповідно до формули

,

де функція визначена на відрізку , причому й .

У випадку застосування заміни змінної в визначеному інтегралі не треба вертатися до первісної змінного, як це робиться при обчисленні невизначеного інтеграла.

Приклади:

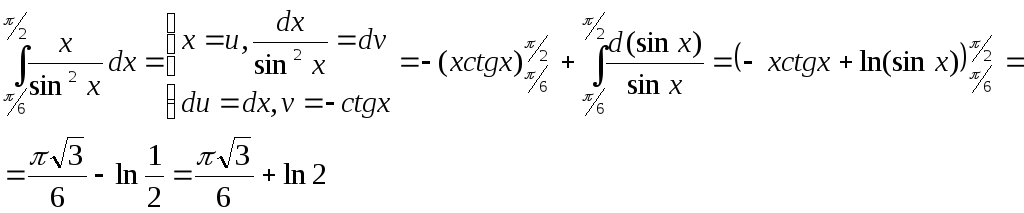
Завдання для самоперевірки:

1. Поняття визначеного інтеграла

2. Геометричний зміст визначеного інтеграла

3. Властивості визначеного інтеграла.

4. Формула Ньютона - Лейбниця

5. Обчислити інтеграли:

Література:

4. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.278-292

5. М.І. Шкіль «Математичний аналіз» стр. 335-365

6. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.513-528

Додаткова література:

1. А.Д. Мышкис «Лекции по высшей математике» стр.344-359

2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 467-474