Розділ: «Інтеграл» Лекція

Тема: Метод заміни змінної інтегрування функцій

Ціль: Одержати необхідні навички інтегрування методом заміни змінної

Основні методи інтегрування

Інтегрування методом заміни змінної. У багатьох випадках введення нової змінної дозволяє спростити подінтегральне вираження й звести інтеграл до лінійної комбінації табличних. Суть методу зводиться до вдалої заміни змінній інтегрування х функцією, диференцьованой на деякому проміжку. Тоді

, де .

Наприклад, при рішенні інтеграла зручно проробити тригонометричну заміну: . Тоді підкореневе вираження приймає вид

, так що

. Застосовуючи тригонометричну формулу зниження ступеня: , одержимо

.

Остаточно, вертаючись до змінного х

.

Часткою случаємо є лінійна заміна змінної: якщо , те .

Приклади:

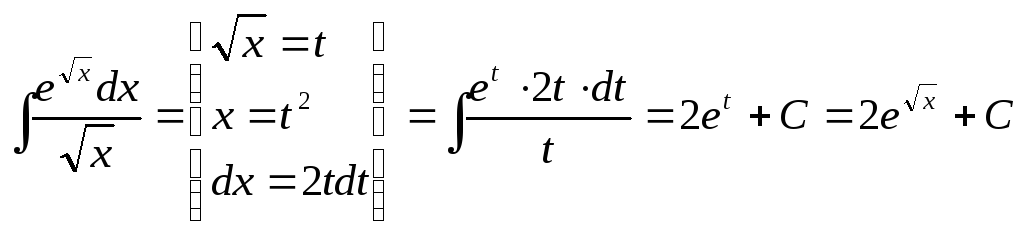
Завдання для самоперевірки:

Знайти інтеграли методом заміни змінної:

Література:

4. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.254-258

5. М.І. Шкіль «Математичний аналіз» стр. 290-294

6. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.503-506

Розділ: «Інтеграл» Лекція

Тема: Метод інтегрування вроздріб

Ціль: Одержати необхідні навички інтегрування методом інтегрування вроздріб

Основні методи інтегрування

Метод інтегрування вроздріб заснований на формулі диференціювання добутку двох функцій. Нехай і – дві диференцьовані функції на проміжку Х. Тоді на Х виконується формула інтегрування вроздріб

.

Ця формула дозволяє звести знаходження невизначеного інтеграла до невизначеного інтеграла , що може виявитися більше простим. Метод інтегрування вроздріб можна застосовувати неодноразово. Іноді цей метод комбінують із методом заміни змінної.

Приклади:

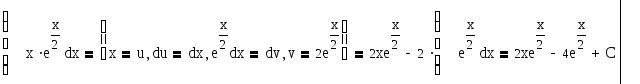
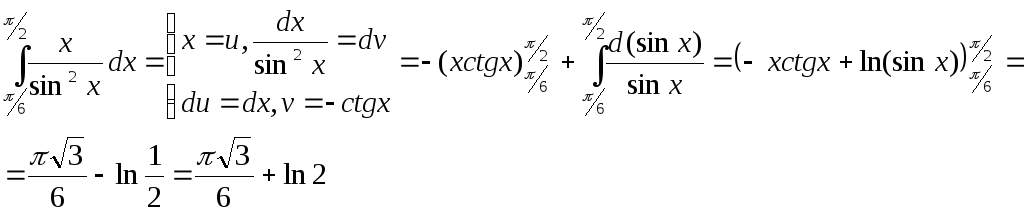
Завдання для самоперевірки:

Знайти інтеграли методом заміни змінної:

Література:

7. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.258-263

8. М.І. Шкіль «Математичний аналіз» стр. 294-299

9. В.М. Лейфура, Г.І. Городницький, Й.І. Фауст «Математика» стр.510-513

Додаткова література:

1. А.Д. Мышкис «Лекции по высшей математике» стр.329-330

2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 387-389

Розділ: «Інтеграл» Лекція

Тема: Інтегрування раціональних дробів

Ціль: Одержати необхідні навички інтегрування раціональних дробів і тригонометричних функцій

План: 1. Інтегрування раціональних дробів

2. Інтегрування тригонометричних функцій

Основні методи інтегрування

Інтегрування раціональних функцій. Раціональним дробом називається функція, яку можна записати у вигляді відносини двох багаточленів: . Якщо цей дріб неправильна, тобто ступінь багаточлена не менше ступеня багаточлена , то можна виконати ділення з остачею й представити у вигляді суми деякого багаточлена й правильного дробу.

У курсі алгебри доводиться теорема, що всякий правильний дріб може бути представлена у вигляді суми найпростіших дробів виду

,

де A, M, N, a, p, q – дійсні числа.

Наприклад, раціональний дріб може бути представлена відповідно до останньої теореми сумою найпростіших дробів

.

Невідомі коефіцієнти розкладання А, В, С і знаходять прийомом, називаним методом невизначених коефіцієнтів: приводять праву частину до загального знаменника й дорівнюють чисельники

,

звідки .

Таким чином, шукане розкладання на найпростіші дроби має вигляд

,

так що інтеграл від цієї функції представляється у вигляді суми інтегралів, які легко перебувають

.

Інтегрування ірраціональних функцій. У ряді випадків інтеграли від ірраціональних функцій за допомогою відповідних підстановок (заміни змінної) раціоналізуються, тобто зводяться до інтегралів від раціональних функцій. Наприклад, для інтеграла , де т – натуральне число; a, b, c, d – речовинні числа, що раціоналізує є підстановка . При цьому виходить інтеграл

,

де – раціональна функція аргументу t.

Інтегрування тригонометричних функцій. Всі тригонометричні функції раціонально (тобто за допомогою одних тільки арифметичних дій) виражаються через синус і косинус; отже, усяка функція, що раціонально залежить від тригонометричних функцій, може бути перетворена у відповідну раціональну функцію тільки від синуса й косинуса. Тому досить розглянути правило інтегрування функцій типу . Інтеграл виду за допомогою універсальної тригонометричної підстановки приводиться до виду

,

де – інша раціональна функція аргументу t.

Поняття про «» інтеграли, що неберуться. З основних правил диференціювання треба, що операція диференціювання елементарної функції приводить знову до елементарної функції. Операція інтегрування такою властивістю не володіє: первісні деяких елементарних функцій уже не є елементарними функціями. Із цієї причини відповідні невизначені інтеграли називаються «неберущимися» в елементарних функціях, а самі функції – не інтегрувальними в кінцевому виді. Такі, наприклад, функції й ін. Проте, первісні цих функцій існують і відіграють значну роль у математику й додатках. Укажемо деякі з них: – інтеграл помилок, що є одним з найважливіших у теорії ймовірностей і статистику, – інтегральний синус, – інтеграл Френеля. Властивості цих функцій вивчені за допомогою наближених розрахунків, існують таблиці їхніх значень, побудовані їхні графіки й т.п.

Помітимо, що рішення задачі знаходження невизначених інтегралів можна полегшити, застосовуючи комп'ютерні програми, наприклад, Mathcad. У цю програму убудований символьний процесор, що дозволяє, зокрема, знаходити похідні й первісні функції.

Приклади:

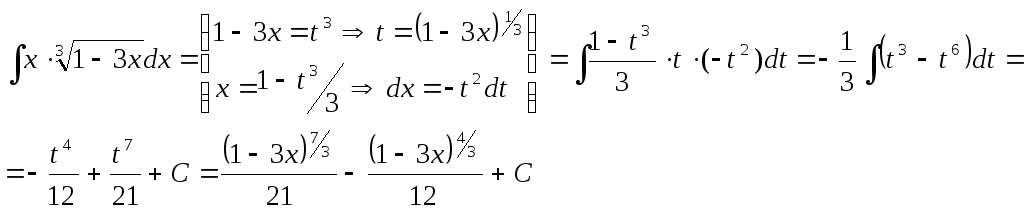
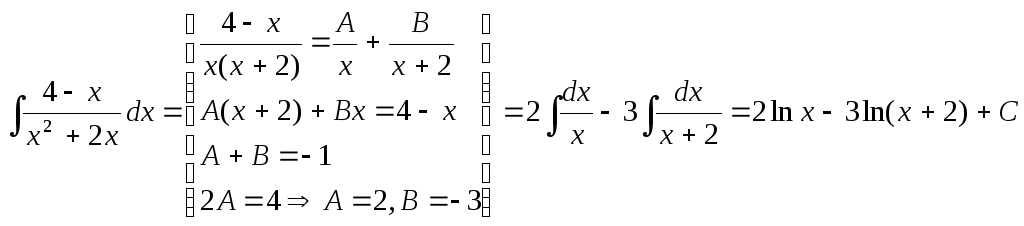
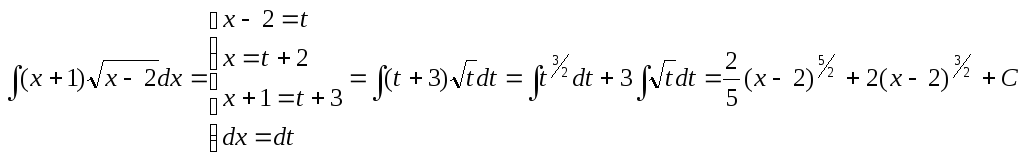d)

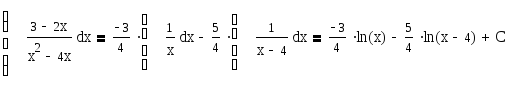
Завдання для самоперевірки:

Знайти інтеграли методом заміни змінної:

Література:

2. «Высшая математика для экономистов» под редакцией Н.Ш. Кремера стр.263-267

3. М.І. Шкіль «Математичний аналіз» стр. 299-315

Додаткова література:

1. А.Д. Мышкис «Лекции по высшей математике» стр.333-335

2. Л.Д. Кудрявцев «Курс математического анализа» том 1 стр. 412-416