
- •Контрольная работа
- •1 Первообразная и неопределенный интеграл
- •1. Интегрирование подстановкой
- •2. Интегрирование по частям
- •3. Интегрирование простейших дробей
- •Контрольные варианты к задаче 11.
- •2 Определенный интеграл и его геометрический смысл
- •Контрольные варианты к задаче 12.
- •Контрольные варианты к задаче 13.
- •Вычисление объема тела вращения
- •Контрольные варианты к задаче 14.
Контрольные варианты к задаче 11.
ЗАДАНИЕ. Вычислить неопределенные интегралы:
1.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
,
4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() , 7)
, 7)
![]() .
.
2.
1)
![]() ,
2)
,
2)
![]() , 3)
, 3)
![]() ,
,
4)
![]() ,
5)
,
5)
![]() , 6)
, 6)
![]() 7)
7)
![]() ,
,
3.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() , 4)
, 4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
4.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
,4)
,
,4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
5.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() , 6)
, 6)
![]() 7)
7)![]() .
.
6.
1)
![]() ,
2)
,
2)
![]() , 3)
, 3)
![]() , 4)
, 4)
![]() ,
,
5)
![]() , 6)
, 6)
![]() ,
7)
,
7)
![]() .
.
7.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() 6)
6)![]() 7)
7)
![]() .
.
8.
1)
![]() , 2)
, 2)
![]() 3)
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
9.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
10.
1)
![]() ,
2)
,
2)
![]() , 3)
, 3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
11.
1)
![]() ,
2)
,
2)![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
12.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
13.
1)![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
14.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
15.
1)
![]() ,
2)
,
2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() .
.
16.
1)
![]() , 2)
, 2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() , 7)
, 7)
![]() .
.
2 Определенный интеграл и его геометрический смысл
Пусть
функция
![]() является первообразной для функции
является первообразной для функции
![]() в некотором промежутке X,
а числа
в некотором промежутке X,
а числа
![]() и
и
![]() принадлежат этому промежутку.
принадлежат этому промежутку.
Определение.
Приращение
![]() любой из первообразных функций
любой из первообразных функций
![]() при изменении аргумента от
при изменении аргумента от
![]() до
до
![]() называется определенным
интегралом
от
называется определенным
интегралом
от
![]() до
до
![]() функции
функции
![]() и обозначается
и обозначается
![]() .
.
Числа
![]() и
и
![]() называются пределами интегрирования:
называются пределами интегрирования:
![]() нижним,
нижним,
![]() верхним.
Отрезок
верхним.
Отрезок
![]() называется отрезком
интегрирования.
Функция
называется отрезком
интегрирования.
Функция
![]() называется подынтегральной
функцией,
а переменная
называется подынтегральной
функцией,
а переменная
![]() переменной
интегрирования.
Таким образом, по определению,
переменной
интегрирования.
Таким образом, по определению,
![]() (2.4)
(2.4)
Равенство (2.1) называется формулой Ньютона-Лейбница.
Существует и другой подход к введению понятия определенного интеграла, основанный на рассмотрении пределов интегральных сумм, который в большей степени приспособлен для приложений. Рассмотрим его на примере вычисления площади криволинейной трапеции.
П усть
дана фигура, ограниченная графиком
непрерывной и неотрицательной функции
усть
дана фигура, ограниченная графиком
непрерывной и неотрицательной функции
![]() ,
отрезком
,
отрезком
![]() и прямыми
и прямыми
![]() ;
;
![]() (рис. 1). Такую фигуру называют криволинейной
трапецией. Найдем ее площадь.
(рис. 1). Такую фигуру называют криволинейной
трапецией. Найдем ее площадь.
Заметим,
что на отрезке
![]() можно указать такую точку
можно указать такую точку
![]() ,
что площадь
,
что площадь
![]() криволинейной трапеции равна
криволинейной трапеции равна
![]() .
(2.5)
.
(2.5)
Действительно,
пусть
![]() наибольшее значение функции
наибольшее значение функции
![]() на отрезке
на отрезке
![]() ,
а
,
а
![]() наименьшее.
Проведем прямые
наименьшее.
Проведем прямые
![]() и
и
![]() .
Тогда криволинейная трапеция целиком
содержится в прямоугольнике
.
Тогда криволинейная трапеция целиком
содержится в прямоугольнике
![]() и содержит целиком прямоугольник
и содержит целиком прямоугольник
![]() (рис. 2).
(рис. 2).
Поэтому
![]() или
или
![]() ,
т.к.
,
т.к.
![]() ;
;
![]() .
Возьмем число
.
Возьмем число
 и
и
![]() .
.
На
отрезке
![]() возьмем такую точку
возьмем такую точку
![]() ,
что
,
что
![]() .
Так как функция
.
Так как функция
![]() непрерывна на
непрерывна на
![]() ,
то каждому значению функции
,
то каждому значению функции
![]() соответствует хотя бы одно значение ее
аргумента
соответствует хотя бы одно значение ее
аргумента
![]() ,
лежащего внутри отрезка
,
лежащего внутри отрезка
![]() .
Тогда
.
Тогда
![]() .
Данное свойство называется теоремой
о среднем.
.
Данное свойство называется теоремой
о среднем.
 Найдем
теперь площадь криволинейной трапеции
Найдем
теперь площадь криволинейной трапеции
![]() через определенный интеграл. Разобьем
криволинейную трапецию на
через определенный интеграл. Разобьем
криволинейную трапецию на
![]() полос так, как показано на рис. 3. При
этом на отрезке
полос так, как показано на рис. 3. При
этом на отрезке
![]() появились точки
появились точки
![]() ,
,
![]() ,...,
,...,
![]() .
.
В
соответствии с формулой (2.5) найдем для
первой полосы точку
![]() ,
,
![]() такую, что площадь первой полосы равна
такую, что площадь первой полосы равна
![]() .
Для второй полосы найдем точку
.
Для второй полосы найдем точку
![]() ,
,
![]() такую, что площадь полосы равна
такую, что площадь полосы равна
![]() .
Поступаем так для всех
.
Поступаем так для всех
![]() полос, т.к. площадь криволинейной трапеции
равна сумме площадей полос, на которую
она разбита:
полос, т.к. площадь криволинейной трапеции
равна сумме площадей полос, на которую
она разбита:
![]() .
.
Такого
типа равенство будет иметь место, как
бы мы не разбивали криволинейную трапецию
на полосы. Длину наибольшего из отрезков
обозначим через
![]() .
Перейдем в нем к пределу при
.
Перейдем в нем к пределу при
![]() ,
получим
,
получим
![]() .
.
Обозначим
![]() ,
,
через
выражение
 получим
получим
![]() .
(2.6)
.
(2.6)
Таким образом, ввели определенный интеграл через предел особого рода сумм (интегральных сумм).
Определение.
Пусть дана функция
![]() ,
определенная на отрезке
,
определенная на отрезке
![]() ,
где
,
где
![]() .
Выполним следующие операции:
.
Выполним следующие операции:
1.Разобьем
отрезок
![]() на
на
![]() частей точками
частей точками
![]()
![]() ,
так что
,
так что
![]() .
.
2.Величину
![]() назовем шагом разбиения.
назовем шагом разбиения.
3.На
каждом из отрезков
![]() зафиксируем произвольную точку
зафиксируем произвольную точку
![]() ,
,
![]() .
.
4.Составим
сумму всех произведений
![]() ,
,
![]() ;
;
![]() или в сокращенном виде
или в сокращенном виде
 ,
(2.7)
,
(2.7)
где
![]() .
.
Суммы
вида (1.7) называются интегральными
суммами функции
![]() .
.
Очевидно,
что при различных разбиениях отрезка
![]() на части получим различные интегральные
суммы вида (2.4). Таким образом, для данной
функции
на части получим различные интегральные
суммы вида (2.4). Таким образом, для данной
функции
![]() и данного отрезка
и данного отрезка
![]() можно составить бесконечное множество
интегральных сумм вида (2.4), которые
зависят от числа
можно составить бесконечное множество
интегральных сумм вида (2.4), которые
зависят от числа
![]() и от выбора точек деления
и от выбора точек деления
![]() и точек
и точек
![]() .
В примере вычисления площади криволинейной
трапеции точки
.
В примере вычисления площади криволинейной
трапеции точки
![]() подбирались специально, что не противоречит
определению определенного интеграла
через пределы интегральных сумм.
подбирались специально, что не противоречит
определению определенного интеграла
через пределы интегральных сумм.
Определение.
Если при
любой последовательности разбиений
отрезка
![]() таких, что
таких, что
![]()
![]() ,
при любом выборе точек
,
при любом выборе точек
![]() интегральная сумма
интегральная сумма
 стремится
к одному и тому же конечному числу
стремится
к одному и тому же конечному числу
![]() :
:![]() ,
то число
,
то число
![]() называется определенным
интегралом
от функции
называется определенным
интегралом
от функции
![]() на отрезке
на отрезке
![]() и обозначается
и обозначается
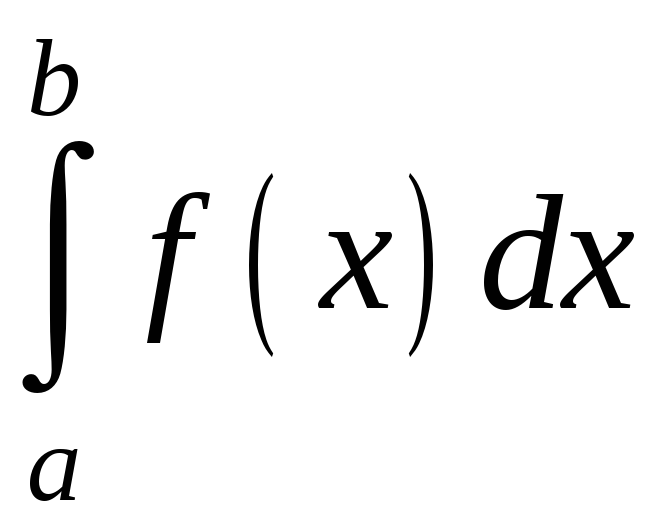 .
Итак, по определению,
.
Итак, по определению,
 .
(2.8)
.
(2.8)
Заметим
без доказательств, что предел в правой
части равенства (2.8) существует и конечен,
если
![]() непрерывна на отрезке
непрерывна на отрезке
![]() .
.
Если
![]() непрерывна и неотрицательна, то
определенный интеграл
непрерывна и неотрицательна, то
определенный интеграл
 численно равен площади криволинейной
трапеции, ограниченной графиком функции
численно равен площади криволинейной
трапеции, ограниченной графиком функции
![]() ,
осью абсцисс и прямыми
,
осью абсцисс и прямыми
![]() ;
;
![]() (см. рис. 1), т.е.
(см. рис. 1), т.е.
 .
(2.9)
.
(2.9)
В этом заключается геометрический смысл определенного интеграла. Без доказательства заметим, что оба определения эквивалентны. Второе определение помогает получить приложение определенного интеграла (вычисление площади и т.д.), а формула Ньютона - Лейбница позволяет вычислить определенный интеграл без вычисления предела интегральной суммы.
Пример
4. Вычислить
 .
.
Решение. Используя правила 1 и 2, представим определенный интеграл в виде суммы трех более простых интегралов, к каждому из которых применим формулу Ньютона-Лейбница:





![]() .
.
Пример
5. Вычислить
![]() .
.
Решение.
Положим
![]() ;
;
![]() ,
тогда
,
тогда
 ,
, .
.
Следовательно,




![]() .
.
Пример
6. Вычислить![]() .
.
Решение.
Сделаем замену
![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Новые пределы интегрирования находим
из соотношения
.
Новые пределы интегрирования находим
из соотношения
![]() ;
если
;
если
![]() ,
то
,
то
![]() ;
если
;
если
![]() ,
то
,
то
![]() .
.
Поэтому


![]()
![]()
Задача 2
1)
Вычислить
 .
.
Решение.
Сделаем замену
![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Новые пределы интегрирования находим
из соотношения
.
Новые пределы интегрирования находим
из соотношения
![]() ;
если
;
если
![]() ,
то
,
то
![]() ;
если
;
если
![]() ,
то
,
то
![]() .
Таким образом, изменению переменной от
.
Таким образом, изменению переменной от
![]() до
до
![]() соответствует изменение переменной
соответствует изменение переменной
![]() от
от
![]() до
до
![]() .
Поэтому
.
Поэтому
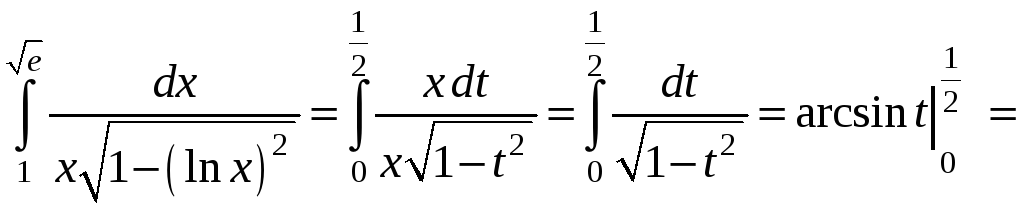
![]()
![]()
2)
Вычислить
 .
.
Решение.
Положим
![]() ,тогда
,тогда
![]() ;
;
![]() ;
;
![]() .
Новые пределы интегрирования находим
из соотношения
.
Новые пределы интегрирования находим
из соотношения
![]() ;
если
;
если
![]() ,
то
,
то
 ;
если
;
если
![]() ,
то
,
то
![]() .
Таким образом, изменению переменной x
от
.
Таким образом, изменению переменной x
от
![]() до x=2
соответствует изменение переменной
до x=2
соответствует изменение переменной
![]() от
от
![]() до
до
![]() .
Следовательно,
.
Следовательно,


![]()
3)
Вычислить
 .
.
Решение.
Положим
![]() ,
тогда
,
тогда
![]() ;
;
![]() ;
;
![]() .
Новые пределы интегрирования находим
из соотношения
.
Новые пределы интегрирования находим
из соотношения
![]() ;
если
;
если
![]() ,
то
,
то
![]() ;
если
;
если
![]() ,
то
,
то
![]() .
Таким образом, изменению переменной
.
Таким образом, изменению переменной
![]() от
от
![]() до
до
![]() соответствует изменение переменной
соответствует изменение переменной
![]() от
от
![]() до
до
![]() ,
следовательно,
,
следовательно,

![]()
