7.Поле равномерно движущегося точечного заряда в вакууме. Принцип суперпозиции для . Силовые линии магнитного поля.

Магнитное поле, создаваемое несколькими движущимися зарядами или токами = векторной суме полей, создаваемых каждым из зарядов или токов в отдельности.

Силовыми линиями называются линии, проведенные в поле так, что касательные к ним в каждой точке совпадают по направлению с вектором магнитной индукции

8 Закон Био–Савара–Лапласа

Найдём выражение для расчёта индукции магнитного поля, созданного током I.В элементарном участке проводника dl содержится n^.dl^.S свободных носителей заряда, где n – концентрация свободных носителей заряда, dl – длина элементарного участка проводника, S – площадь поперечного сечения проводника.Каждый из зарядов создаёт в интересующей нас точке магнитное поле, индукция которого

где v – скорость направленного движения свободных носителей заряда. Умножив В на количество свободных носителей заряда в элементе проводника dl, получим индукцию магнитного поля, созданную этим элементом проводника с током,

поскольку env = j*,

;поскольку dl^.j = dl^.j (dl и j совпадают по направлению),

.

Таким образом, индукция магнитного поля, созданного элементом dl проводника с током I на расстоянии r от элемента проводника, определяется выражением

.

Это выражение и представляет собой закон Био–Савара–Лапласа.

Из закона видно, что вектор магнитной индукции dB всегда перпендикулярен плоскости, в ко-торой лежат векторы dl и r. Его направление определяется по правилу правого винта.

Модуль вектора dB определяется из выражения

,

где  – угол между векторами dl и r. Пример в тетради

9, количество силовых линий магнитного поля, входящих в замкнутый объём, всегда равно количеству линий, выходящих из него.

Но это означает, что суммарный поток вектора магнитной индукции через замкнутую поверхность равен нулю- теорема Г.

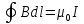
Циркуляция В по произвольному контуру равна произведению на алгебраическую сумму токов, охватываемых контуром.

Найдем циркуляцию вектора В вдоль произвольной линии магнитной индукции –окружности радиуса r Во всех точках линии индукции вектор В равен по модулю и направлен по касательной к этой линии, так что . Следовательно,

10.

11. 11. Сила Лоренца.

Если на движущуюся частицу с электрическим зарядом q одновременно действуют и магнитное, и электрическое поля, то результирующая сила F , называемая силой Лоренца, равна сумме двух составляющих–магнитной и электрической:

Модуль силы Лоренца

,

где  – угол между векторами v и B.

Направление силы Лоренца зависит от направления вектора . Его можно определить с помощью правила правого винта или правила левой руки.

13.Сила, действующая на контур с током со стороны однородного магнитного поля.

Магнитное поле оказывает ориентирующее действие на контур.

Рис. 21.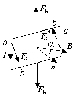

В отсутствие тока рамка находится в положении равновесия. При пропускании постоянного тока через рамку

она поворачивается под действием сил ампера так, сто ее плоскость располагается перпендикулярно вектору В, причем из конца вектора В ток в рамке виден идущим против часовой стрелки.

Рис.21.9

F₁=F₃=Iab

и направлены вдоль вертикальной оси рамки в противоположные стороны, поэтому они полностью уравновешивают друг друга.

14. Силы, действующие на стороны а контура, стремятся повернуть контур так, чтобы вектор n был параллелен вектору В (вектор n – единичный вектор, направление которого совпадает с положительной нормалью к контуру).

Модули этих сил равны F_a = IaB. Силы и создают момент пары сил, модуль которого равен

М = F_absin = IabB sin = IBSsin,

где S – площадь контура;  – угол между вектором F_a и продолжением стороны b контура; этот угол равен по величине углу между единичным вектором n и вектором В.

В векторной форме данное выражение имеет вид

.

где n – единичный вектор, направленный по положительной нормали к контуру.

Выражение для момента сил можно записать и в такой форме:

M = [p_m,B],

где p_m = ISn – магнитный момент контура с током; направление магнитного момента совпадает с положительной нормалью к контуру.

15.-модуль силы ампера

Работа при перемещении перемычки на величину dx

dS=ldx

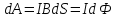
dФ- магнитный поток сквозь поверхность,

В данном случае dФ есть поток вектора магнитной индукции через площадь, пройденную перемычкой в процессе её движения.

Теперь рассмотрим жёсткий замкнутый контур с током I, перемещающийся в магнитном поле.

Выделим бесконечно малый элемент контура dl. При его перемещении на расстояние dh магнитное поле совершает работу А = IdФ, где А – работа по перемещению элемента контура dl на расстояние dh, а dФ – поток вектора магнитной индукции через площадь, пройденную элементом контура dl.

Работа по перемещению всего контура на dh

,

где dФ – магнитный поток через площадь, пройденную всеми элементами контура dl

Работа по перемещению контура на конечное расстояние

,

где Ф₂ и Ф₁ – значения магнитного потока через контур в начальном и конечном положениях контура.

16 Поле в магнетиках. Механизм намагничения. Вектор намагниченности . Токи намагничивания . Теорема о циркуляции вектора намагниченности .

Вещества, способные намагничиваться называются магнетиками. (намагничиваться). Намагниченное вещество создает магнитное поле В', которое накладывается на обусловленное токами поле В₀. Оба поля в сумме дают результирующее поле B=B₀+B^/

Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний. Под В подразумевается усредненное (макроскопическое) поле.

Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые токи (молекулярные

токи). Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего

поля молекулярные токи ориентированы беспорядочным образом,

вследствие чего обусловленное ими результирующее поле равно

нулю. В силу хаотической ориентации магнитных моментов отдельных молекул суммарный магнитный момент тела также равен нулю.

Под действием поля магнитные моменты молекул приобретают

преимущественную ориентацию в одном направлении, вследствие

чего магнетик намагничивается — его суммарный магнитный момент становится отличным от нуля. Магнитные поля отдельных

молекулярных токов в этом случае уже не компенсируют друг

друга и возникает поле В'.

Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность J, равная отношению манитного момента макроскопически малого объема вещества к этому объему , где P_mi – магнитный момент i-го атома из объема .

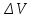Токи намагничивания I' . Намагничивание вещества связано с преимущественной ориентацией магнитных моментов отдельных молекул в одном направлении. Элементарные круговые токи, связанные с каждой молекулой, называются молекулярными. Молекулярные токи оказываются ориентированными, т.е. возникают токи намагничивания -.

Для стационарного случая циркуляция вектора J по контуру равна алгебраической сумме токов намагничивания охватываемых этим контуром.

,