
- •1 Краткое описание устройства и принципа действия разрабатываемого изделия
- •2 Рачетно-конструкторский раздел
- •2.1 Выбор электродвигателя, кинематический и силовой расчеты привода
- •2.2 Расчёт зубчатой передачи редуктора
- •2.3 Расчёт открытой передачи
- •2.4 Предварительный расчет валов редуктора и разработка их эскизов
- •2.5 Расчет конструктивных размеров зубчатой пары редуктора
- •2.6 Расчет конструктивных размеров корпуса редуктора
- •2.7 Первый этап компоновки редуктора
- •2.8 Определение реакций подшипников валов редуктора и построение эпюр изгибающих и крутящих моментов
- •2.9 Подбор и расчет подшипников для валов редуктора
- •2.10 Подбор муфты
- •2.11 Подбор и проверочный расчет шпоночных или шлицевых соединений
- •2.12 Проверочный расчет на сопротивление усталости вала редуктора
- •3 Технологический раздел
- •3.1 Выбор смазки смазка зацепления и подшипников
- •3.2 Описание сборки редуктора
- •Приложение а первый этап компоновки редуктора
2.7 Первый этап компоновки редуктора
Зазор между торцом ступицы колеса и внутренней стенкой корпуса А1, мм определяется по формуле (2.76):
![]() , (2.76)
, (2.76)
где δ – толщина стенок корпуса, мм; δ=8 мм; определена по формуле (2.68).
Подстановкой указанных выше значений в формулу (2.76) получено:
![]() мм.
мм.
При наличии ступицы зазор берется от торца ступицы.
Зазор от окружности вершин зубьев до внутренней стенки корпуса А, мм определяется по формуле (2.77):
![]() , (2.77)
, (2.77)
Подстановкой значений в формулу (2.77) получено:
![]() мм.
мм.
Расстояние между наружным
кольцом подшипника ведущего вала и
внутренней стенкой корпуса А,
принимается
![]() мм.
мм.
Параметры выбранных подшипников легкой серии представлены в таблице 2.1.
Таблица 2.1 – Параметры подшипников легкой серии
|
|
Условное обозначение |
d, мм |
D, мм |
B, мм |
Грузоподъёмность, кН |
|
|
Динамическая С |
Статическая С0 |
|||||
|
Ведущий вал |
208 |
40 |
80 |
18 |
32,0 |
17,8 |
|
Ведомый вал |
213 |
65 |
120 |
23 |
56,0 |
34,08 |
Выбирается способ смазывания
подшипников. Принимается пластичный
смазочный материал. Для предотвращения
вытекания смазки внутрь корпуса и
вымывания пластичного смазочного
материала жидким маслом устанавливаются
мазеудерживающие кольца. Ширина
мазеудерживающих колец определяет
размер
![]() мм.
Принимается y=10
мм.
мм.
Принимается y=10
мм.
2.8 Определение реакций подшипников валов редуктора и построение эпюр изгибающих и крутящих моментов
2.8.1.Ведущий вал
Для построения эпюр необходимы следующие значения:
-
Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40);
-
Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41);
-
Fв – давление на вал; Fв = 1473,8 H; определено по формуле (2.60);
-
d1 – делительный диаметр шестерни – d1 = 58 мм; определен по формуле (2.34);
-
d2 – делительный диаметр колеса – d2 = 222 мм; определен по формуле (2.37).
Расчет сил действующих на валы редуктора для построения эпюр изгибающих моментов определен по формуле (2.78):
![]() , (2.78)
, (2.78)
где Fв – давление на вал; Fв = 1473,8 H; определено по формуле (2.60).
Подстановкой указанных выше значений в формулу (2.78) получено:
![]() Н.
Н.
Реакции подшипников RАy и RВy в вертикальной плоскости находятся решением системы уравнений по формуле (2.79):
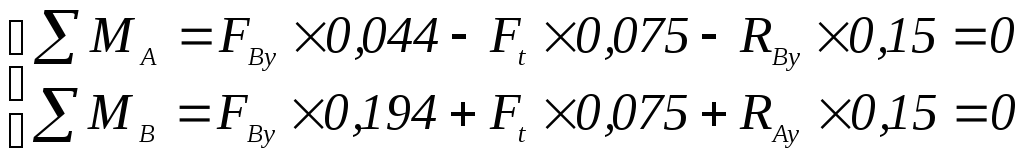 (2.79)
(2.79)
где RВy – реакция точки В, Н; определена по формуле (2.80); представлена на рисунке 2.3;
RАy – реакция точки А, Н; определена по формуле (2.81); представлена на рисунке 2.3;
Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40);
Реакция точки В, RВy Н определяется по формуле(2.80):
![]() , (2.80)
, (2.80)
где Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40).
Подстановкой указанных выше значений в формулу (2.80) получено:
![]() Н.
Н.
Следовательно, реакция точки В направлена в противоположную сторону, RВyист=22300,25 Н.
Реакция точки А, RАy Н определяется по формуле(2.81):
![]() , (2.81)
, (2.81)
где Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40).
Подстановкой указанных выше значений в формулу (2.81) получено:
![]() Н.
Н.
Выполняется проверка суммарных реакций ведущего вала в вертикальной плоскости:
![]() ;
;
Уравнения для построения эпюры изгибающего момента в вертикальной плоскости имеют вид:
-
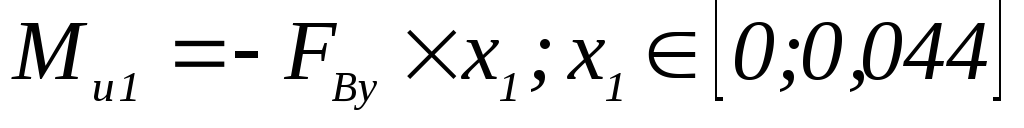 ;
; -
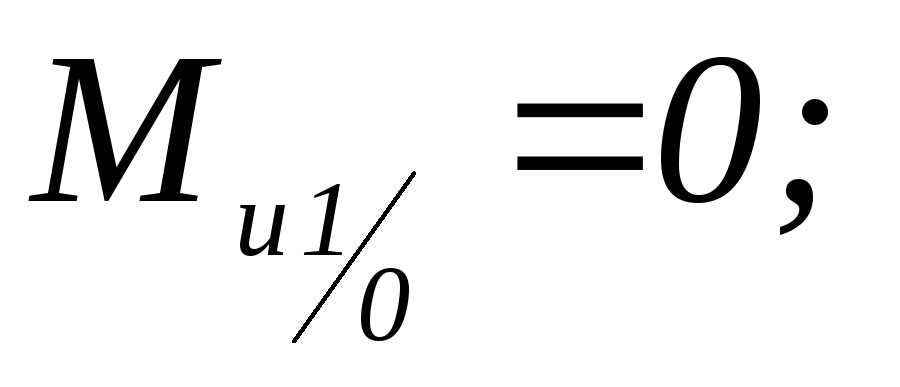
-
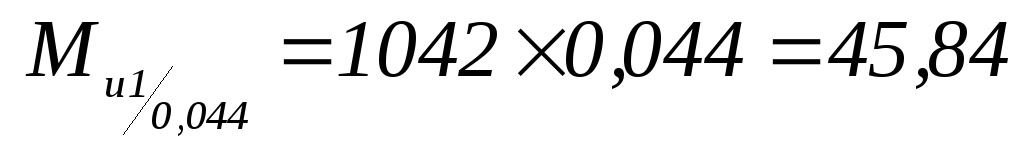 Н×м;
Н×м; -
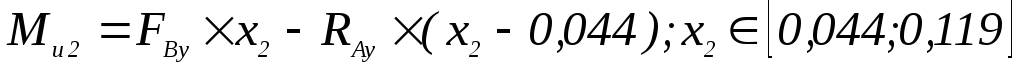 ;
; -
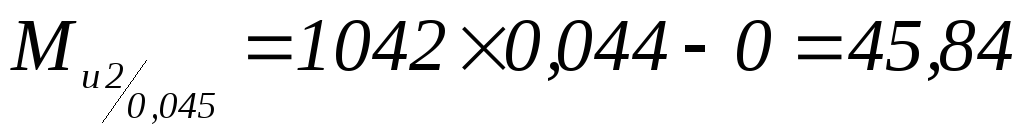 Н×м;
Н×м; -
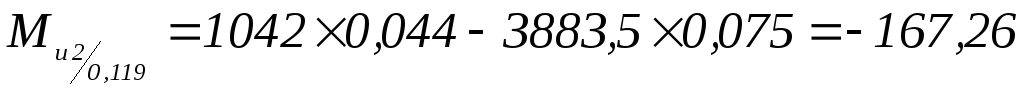 Н×м;
Н×м; -
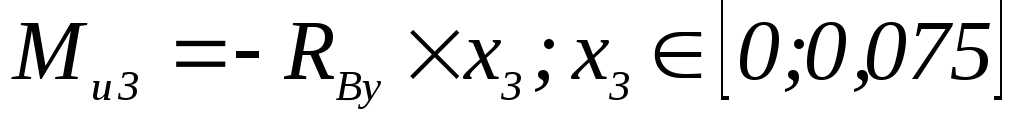 ;
; -

-
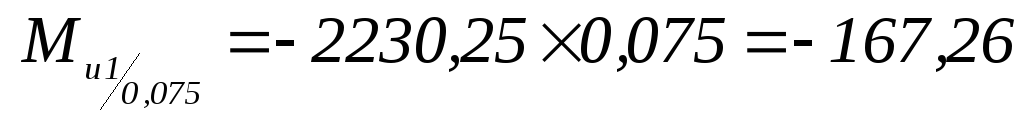 Н×м.
Н×м.
Реакции подшипников RАX и RВX в горизонтальной плоскости находятся решением системы уравнений по формуле (2.82):
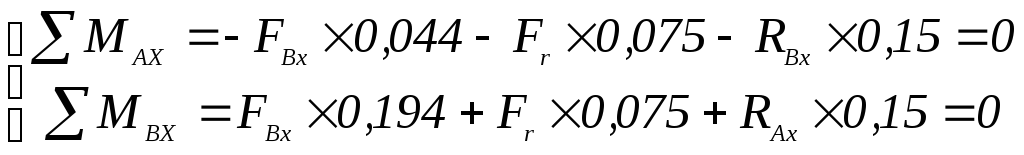 (2.82)
(2.82)
где RВx – реакция точки В, Н; определена по формуле (2.83); представлена на рисунке 2.3;
RАx – реакция точки А, Н; определена по формуле (2.84); представлена на рисунке 2.3;
Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41).
Реакция точки В, RВх Н определяется по формуле(2.83):
![]() , (2.83)
, (2.83)
где Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41).
Подстановкой указанных выше значений в формулу (2.83) получено:
![]() Н.
Н.
Следовательно, реакция точки В направлена в противоположную сторону, RВxист=719,9 Н.
Реакция точки А, RАх Н определяется по формуле(2.84):
![]() , (2.84)
, (2.84)
где Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41).
Подстановкой указанных выше значений в формулу (2.84) получено:
![]() Н.
Н.
Выполняется проверка суммарных реакций ведущего вала в горизонтальной плоскости:
![]() .
.
Уравнения для построения эпюры изгибающего момента в горизонтальной плоскости имеют вид:
-
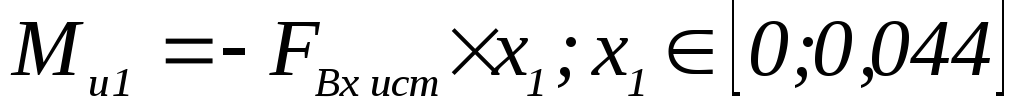 ;
; -
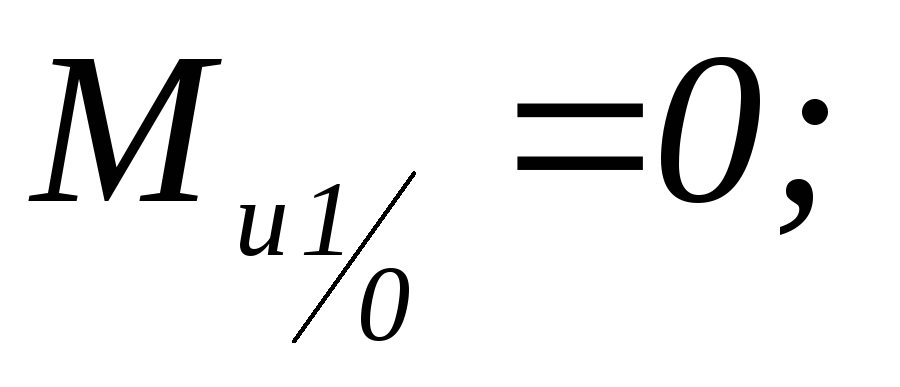
-
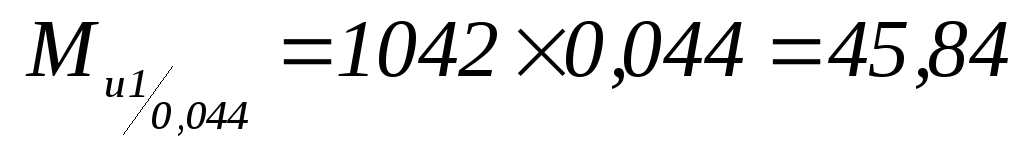 Н×м;
Н×м; -
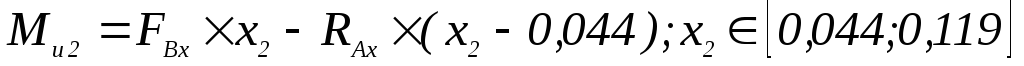 ;
; -
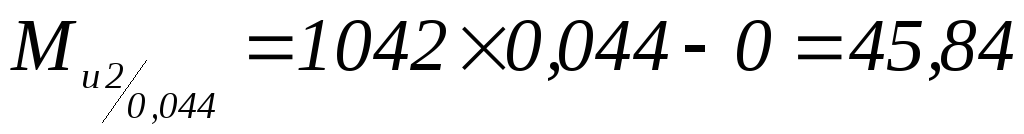 Н×м;
Н×м; -
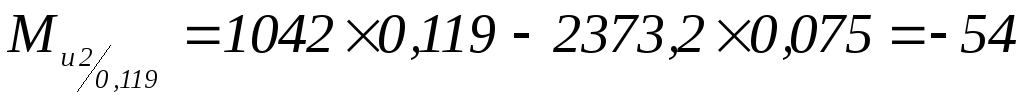 Н×м;
Н×м; -
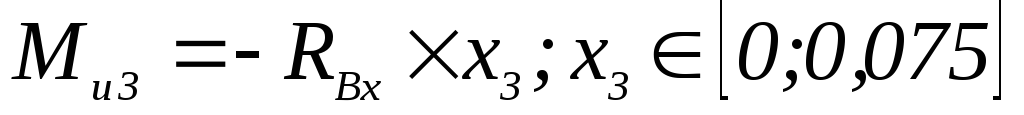 ;
; -
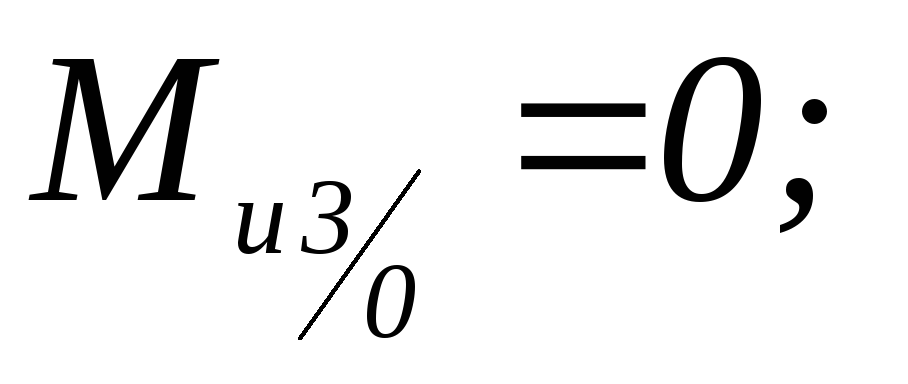
-
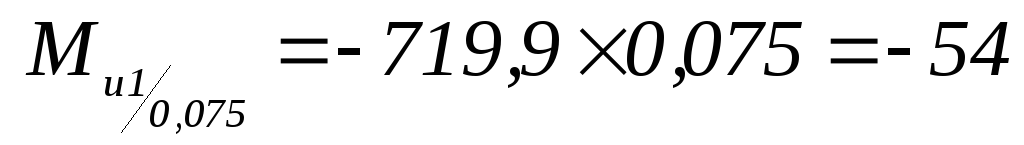 Н×м.
Н×м.
Э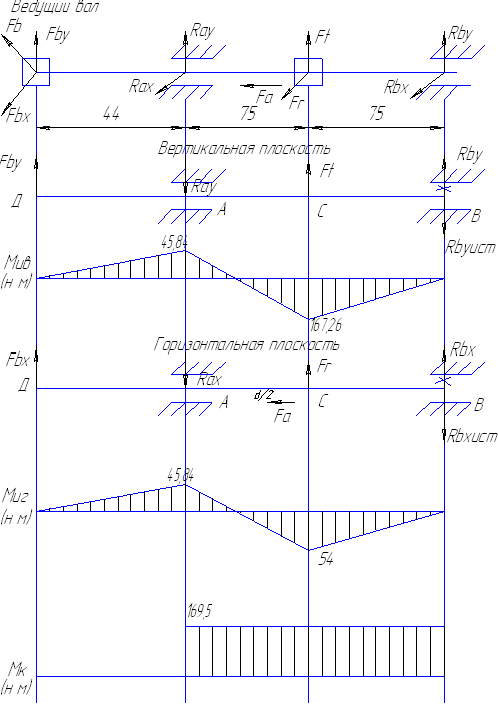 пюры
ведущего вала представлены на рисунке
2.3.
пюры
ведущего вала представлены на рисунке
2.3.
Рисунок 2.3 – Эпюры ведущего вала
2.8.2.Ведомый вал
Реакции подшипников RАy и RВy на ведомом валу в вертикальной плоскости находятся решением системы уравнений по формуле (2.83):
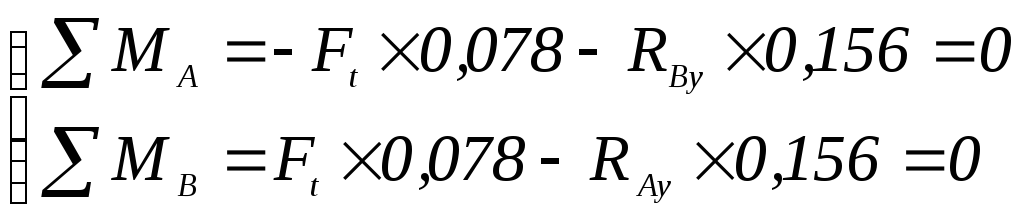 , (2.83)
, (2.83)
где RВy – реакция точки В, Н; определена по формуле (2.84); представлена на рисунке 2.4;
RАy – реакция точки А, Н; определена по формуле (2.85); представлена на рисунке 2.4;
Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40).
Реакция точки В, R2Вy Н определяется по формуле(2.84):
![]() , (2.84)
, (2.84)
где Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40).
Подстановкой указанных выше значений в формулу (2.84) получено:
![]() Н.
Н.
Реакция точки А, RАy,Н определяется по формуле(2.85):
![]() , (2.85)
, (2.85)
где Ft – окружная сила; Ft = 5071,8 H; определена по формуле (2.40).
Подстановкой указанных выше значений в формулу (2.85) получено:
![]() Н.
Н.
Выполняется проверка суммарных реакций ведомого вала в вертикальной плоскости:
![]() .
.
Уравнения для построения эпюры изгибающего момента ведомого вала в вертикальной плоскости имеют вид:
-
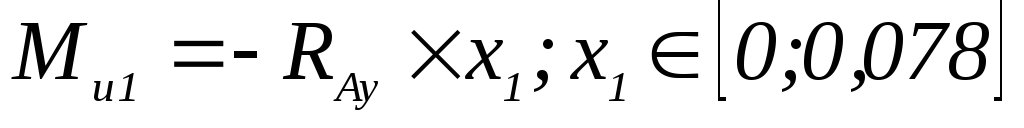 ;
; -
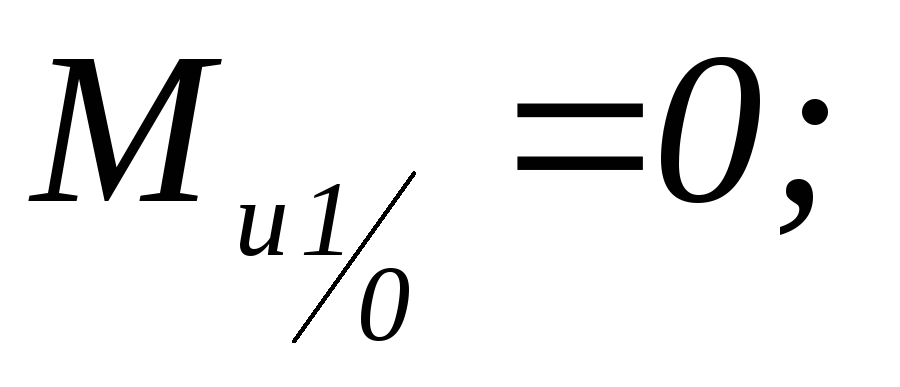
-
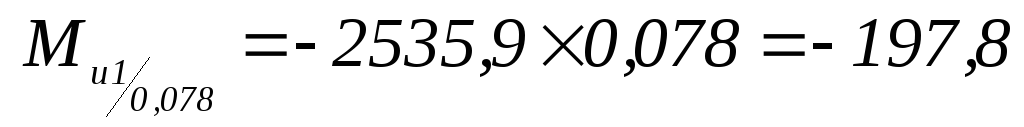 Н×м;
Н×м; -
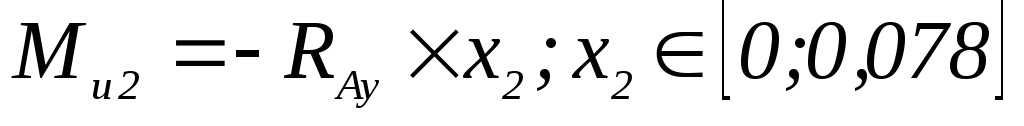 ;
; -
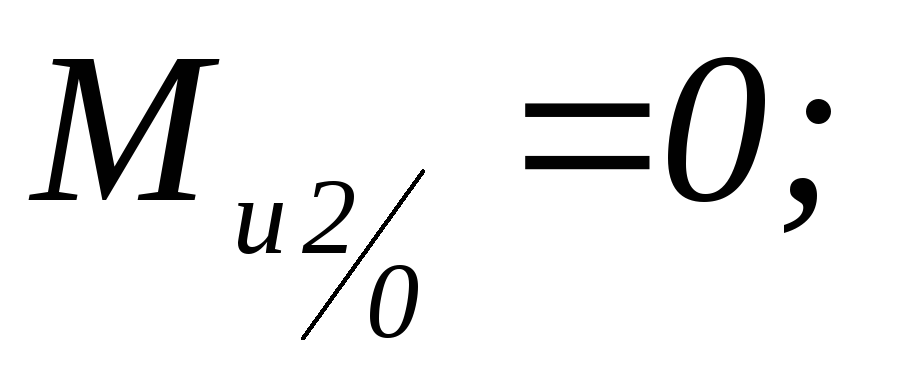
-
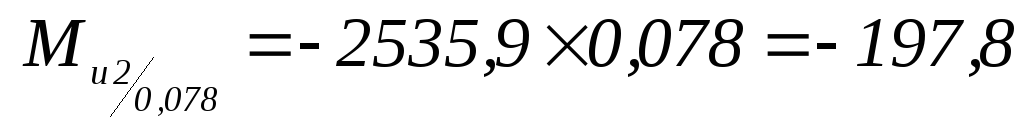 Н×м.
Н×м.
Реакции подшипников RАx и RВx в горизонтальной плоскости находятся решением системы уравнений по формуле (2.86):
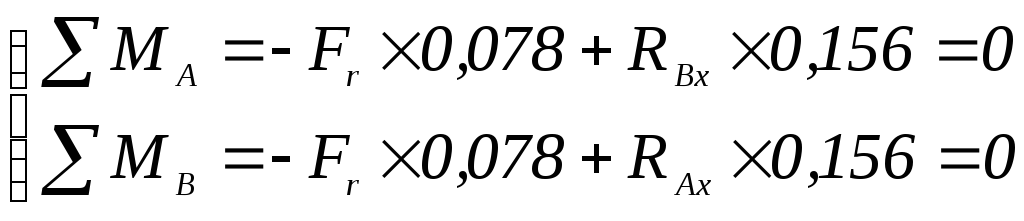 , (2.86)
, (2.86)
где Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41).
Реакция точки В, RВx, Н определяется по формуле(2.87):
![]() , (2.87)
, (2.87)
где Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41).
Подстановкой указанных выше значений в формулу (2.87) получено:
![]() Н.
Н.
Реакция точки А, RАх, Н определяется по формуле(2.88):
![]() , (2.88)
, (2.88)
где Fr – радиальная сила; Fr = 2051,2 H; определена по формуле (2.41).
Подстановкой указанных выше значений в формулу (2.88) получено:
![]() Н.
Н.
Выполняется проверка суммарных реакций ведомого вала в горизонтальной плоскости:
![]() .
.
Уравнения для построения эпюры изгибающего момента в горизонтальной плоскости ведомого вала имеют вид:
-
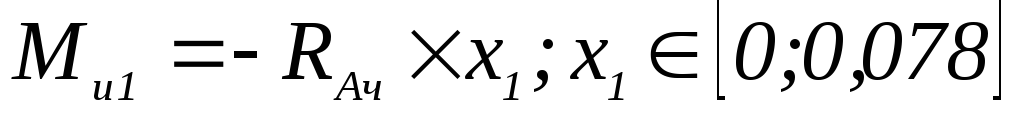 ;
; -
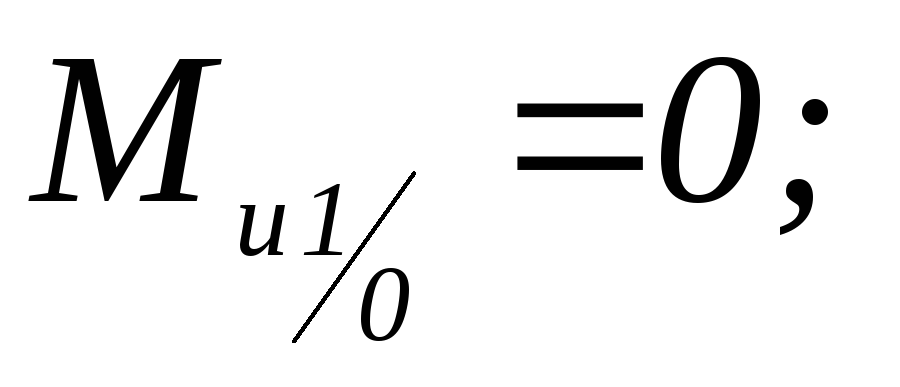
-
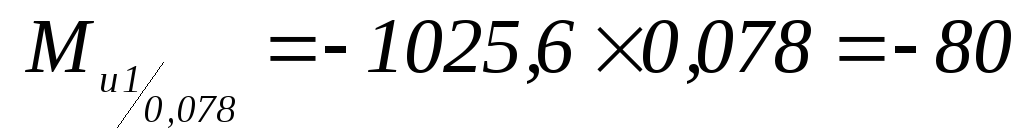 Н×м;
Н×м; -
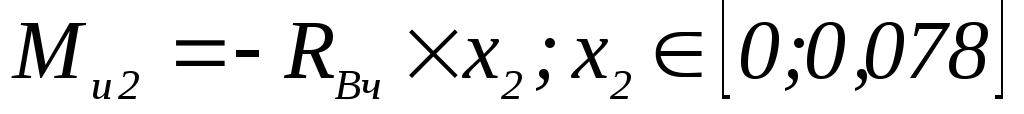 ;
; -
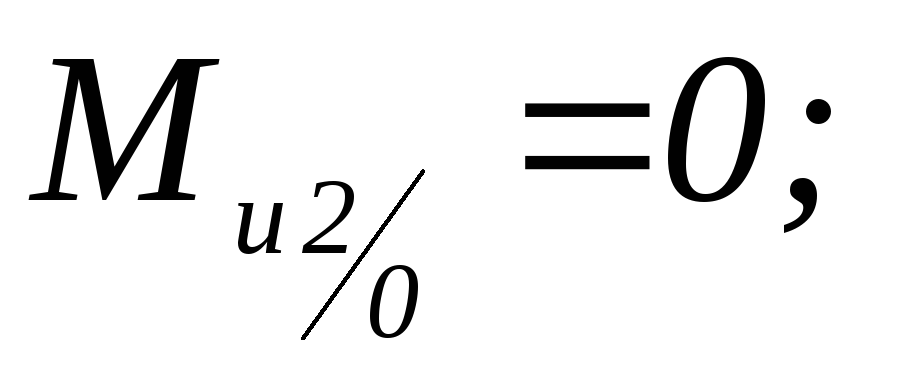
-
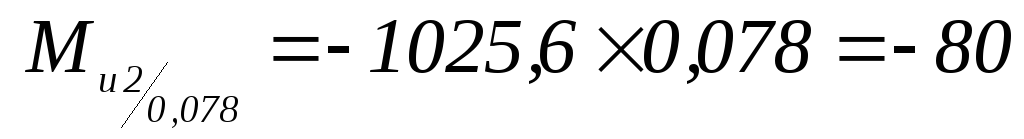 Н×м.
Н×м.
Э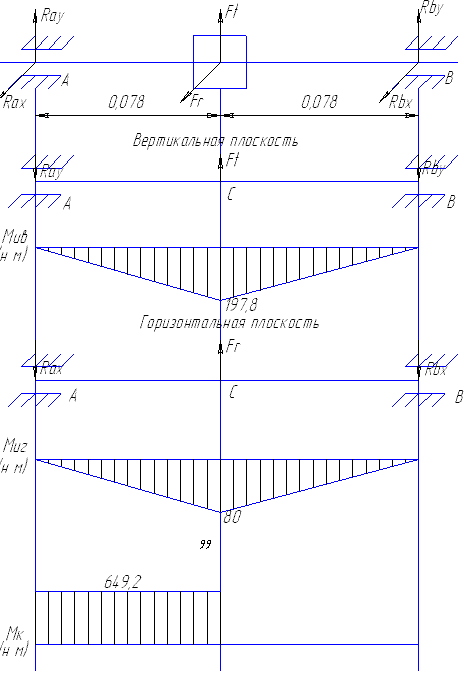 пюры
ведомого вала представлены на рисунке
2.4.
пюры
ведомого вала представлены на рисунке
2.4.
Рисунок 2.4 – Эпюры ведомого вала
Суммарная реакция на ведущем валу в горизонтальной плоскости Pr1, определяется по формуле (2.89):
![]() , (2.89)
, (2.89)
где RAхист – реакция точки A, Н; RAхист=2373,2 Н; определена по формуле (2.84);
R2Ayист – реакция точки A, Н; R2Ayист=3885,5 Н; определена по формуле (2.81).
Подстановкой указанных выше значений в формулу (2.89) получено:
![]() Н.
Н.
Суммарная реакция на ведущем валу в горизонтальной плоскости Pr2 определяется по формуле (2.90):
![]() , (2.90)
, (2.90)
где RBх.ист – реакция точки A, Н; RBх.ист=719,9 Н; определена по формуле (2.83);
RByист – реакция точки A, Н; RByист=2230,25 Н; определена по формуле (2.80).
Подстановкой указанных выше значений в формулу (2.90) получено:
![]() Н.
Н.
Суммарная реакция на ведомом валу в горизонтальной плоскости Pr3, определяется по формуле (2.91):
![]() , (2.91)
, (2.91)
где RAх – реакция точки A, Н; RAх=1025,6 Н; определена по формуле (2.88);
RAyист – реакция точки A, Н; RAy=2535,9 Н; определена по формуле (2.85).
Подстановкой указанных выше значений в формулу (2.91) получено:
![]() Н.
Н.
Суммарная реакция на ведомом валу в вертикальной плоскости Pr4, определяется по формуле (2.92):
![]() , (2.92)
, (2.92)
где RAх – реакция точки A, Н; RAх=1025,6 Н; определена по формуле (2.88);
RAyист – реакция точки A, Н; RAy=2535,9 Н; определена по формуле (2.85).
Подстановкой указанных выше значений в формулу (2.92) получено:
![]() Н.
Н.
