
Типовой расчет №2
Векторная алгебра и аналитическая геометрия.
Типовые примеры.
Задание 1.
Коллинеарны ли
векторы
![]() , построенные по векторам
, построенные по векторам![]()
![]() ={4;
0; 4},
={4;
0; 4},
![]() {-1; 3; 2}
{-1; 3; 2}
![]()
![]()
Решение: При умножении вектора на число его координаты умножаются на это число
Найдем координаты
векторов
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,=
{12; 0; 12}
,=
{12; 0; 12}
![]() ={-9;
27; 18}
={-9;
27; 18}
![]() ={8;
0; 8}
={8;
0; 8}
![]() ={1;
-3;-2}
={1;
-3;-2}
При сложении векторов их координаты складываются Таким образом, получим
![]()
![]()
Два вектора коллинеарны в том и только том случае, когда один из них может быть получен
умножением
другого на некоторое число:
![]()
Векторное равенство
![]()
равносильно трем числовым
![]()
или
![]()
![]() ,
следовательно, векторы
,
следовательно, векторы
![]() неколлинеарны
неколлинеарны
Задание 2
Найти косинус угла
между векторами
![]() ,
если заданы координат точек
,
если заданы координат точек
![]()
Решение
Косинус угла![]() между
векторами
между
векторами
![]() определяется
формулой
определяется
формулой
![]() где
где
![]() -скалярное произведение векторов
-скалярное произведение векторов
![]() -длины
векторов
-длины
векторов
Найдем координаты векторов
![]()
Тогда

Задание 3
Вычислить объем тетраэдра с вершинами в точках
![]()
и его высоту,
опущенную из вершины
![]() на
на
![]()
Решение: известно, что
Vтетр
=![]()
Находим:

Так как
 то V=
то V=![]() куб.ед.
куб.ед.
С другой стороны,
объем тетраэдра равен V=![]()
![]() H,
где
H,
где
![]() -площадь
грани
-площадь
грани
![]() ,
,
H-длина
высоты, опущенной из вершины
![]() на
грань
на
грань
![]()
![]() =
=![]() Находим
Находим

Окончательно имеем:
![]() =
=![]() кв.ед.
кв.ед.

Задание 4.
Структурная матрица торговли трех стран S1, S2, S3 имеет вид:
 .
.
Найти соотношение национальных доходов стран для сбалансированной торговли.
Решение:
Находим собственный
вектор ![]() ,
отвечающий собственному значению
,
отвечающий собственному значению ![]() ,
решив уравнение
,
решив уравнение ![]() =0 или систему
=0 или систему
 =
=![]() методом Гаусса. Найдем
методом Гаусса. Найдем ![]() ,
,
![]() ,
,![]() ,
т.е.
,
т.е.![]() .
Полученный результат означает, что
сбалансированность торговли трех стран
достигается при соотношении национальных
доходов стран
.
Полученный результат означает, что
сбалансированность торговли трех стран
достигается при соотношении национальных
доходов стран ![]() .
.
Задание 5
Даны две
последовательные вершины
![]() ромба АВСD и точка
пересечения
ромба АВСD и точка
пересечения
его диагоналей О![]()
Найти :
-
Длину и уравнение стороны CD
-
Уравнение высоты, проведенной из вершины В
-
Внутренний угол при вершине А
-
Площадь ромба
Решение.
Известно, что точка пересечения диагоналей ромба делит эти диагонали пополам. Найдем
координаты точек С и D, воспользовавшись формулами для координат середины отрезка.
![]()
Следовательно:

-
Длина стороны CD=

Прямая CD проходит через две заданные точки, её уравнение имеет вид

CD: 5х-y-19=0-уравнение стороны CD
-
Угловой коэффициент прямой CD
КCD=![]() из
условия перпендикулярности прямых ВК
и CD КВК=
из
условия перпендикулярности прямых ВК
и CD КВК=![]()
Уравнение высоты имеет вид
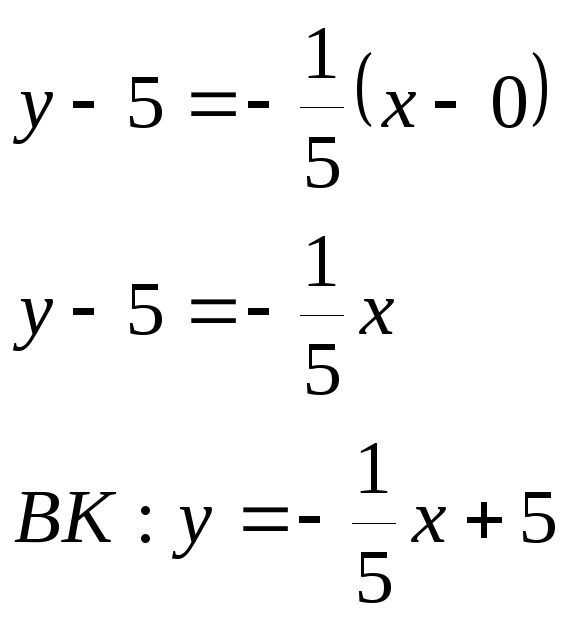
-
Угловой коэффициент прямой AD
К1=![]()
Угловой коэффициент прямой АВ:
К2=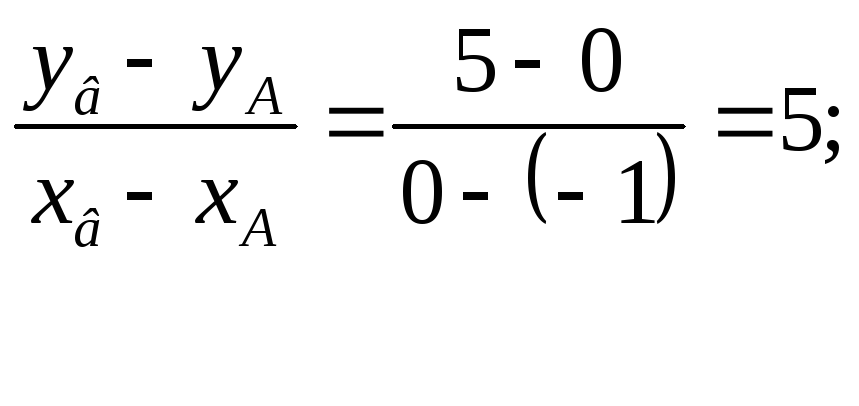
tg
![]()
-
Площадь ромба S=
 ,где
d1 и d2
–диагонали ромба.
,где
d1 и d2
–диагонали ромба.
Найдем длины диагоналей ромба.
d1=AC=![]()
d2=BD=![]()
S1= ед.
ед.
Задание 6
Даны четыре точки
![]() .
Составить уравнения:
.
Составить уравнения:
-
Плоскости

-
Прямой

-
Прямой
 ,
перпендикулярной к плоскости
,
перпендикулярной к плоскости
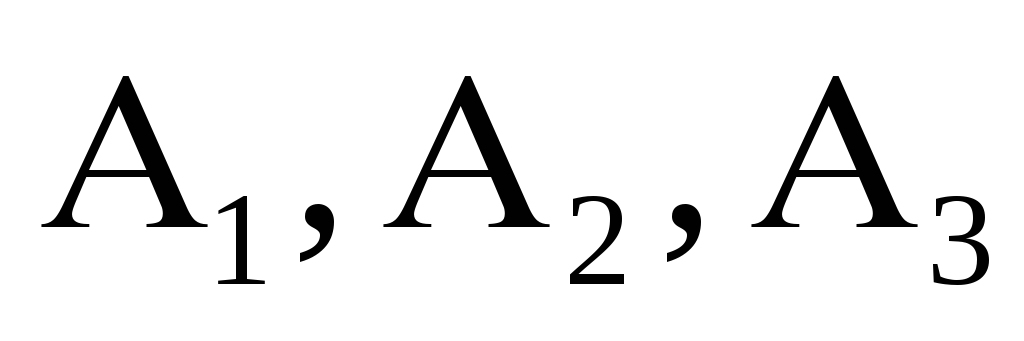
-
Прямой
 ,
параллельно прямой
,
параллельно прямой

-
Плоскости, проходящей через точку
 перпендикулярно
вектору
перпендикулярно
вектору

-
Найти косинус угла между координатной плоскостью Оху и плоскостью

-
Решение :
Используя формулу:

Составляем уравнение
плоскости
![]()

Раскрыв данный определить по элементам первой строки, придем к уравнению
6х - 7y - 9z + 97=0;
-
Учитывая уравнения прямой, проходящей через две точки
![]() ,
уравнение прямой
,
уравнение прямой
![]() можно записать в виде
можно записать в виде
![]()
-
Из условия перпендикулярности прямой
 и
плоскости
и
плоскости
 следует,
следует,
что в качестве направляющего вектора прямой S можно взять нормальный вектор
![]() плоскости
плоскости
![]()
Тогда уравнение
прямой
![]() М
с учетом уравнений
М
с учетом уравнений

запишется в виде
![]()
-
Так как прямая
 параллельна
прямой
параллельна
прямой
 ,
то их направляющие векторы
,
то их направляющие векторы
![]() и
и
![]() можно считать совпадающими:
можно считать совпадающими:
![]() =
=![]() =
=![]()
Следовательно
уравнение прямой
![]() параллельной прямой
параллельной прямой
![]() имеет вид
имеет вид
![]()
-
Если плоскость проходит через точку М0
 и
перпендикулярна к вектору
и
перпендикулярна к вектору
![]() ,
то её уравнение записывается в виде
,
то её уравнение записывается в виде
![]()
Подставляя в это
уравнение вместо х0, y0,
z0 координаты точки
![]() ,
а вместо А, В, С
,
а вместо А, В, С
координаты вектора
![]()
получим уравнение искомой плоскости
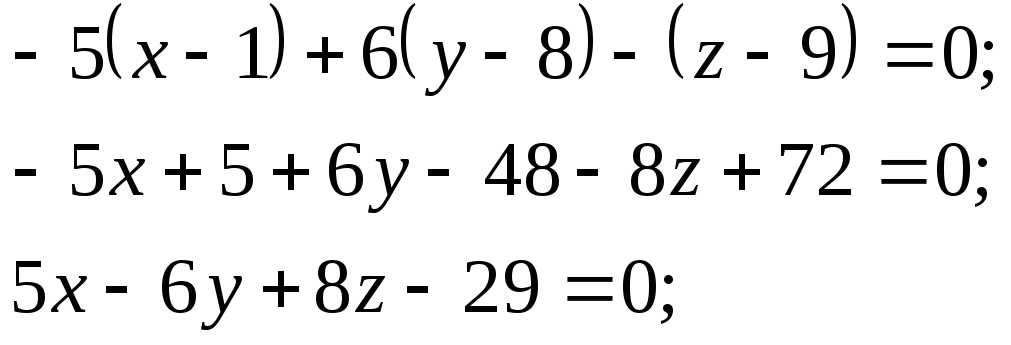
-
Величина угла
 между плоскостями
между плоскостями
А1х + В1y + C1z + D1=0 и А2х + В2y + C2z + D2=0
вычисляется на основании формулы:
cos![]()
![]()
![]()
ЗАДАЧИ
