2.2.Функция распределения Бозе - Эйнштейна

В отличие от классических частиц элементарные частицы микро­мира: фотоны, фононы, электроны, протоны, нейтроны и др. — яв­ляются неразличимыми частицами и, следовательно, в общем случае не подчиняются статистике Максвелла—Больцмана. Распределение таких частиц по энергиям зависит от того, подчиняются ли частицы принципу Паули. Если частицы не подчиняются этому принципу (например, фотоны и фононы), то в данном энергетическом состоянии может находиться неограниченное число частиц. Такие частицы при­нято называть бозонами, а распределение их по энергиям описывается функцией Бозе—Эйнштейна:

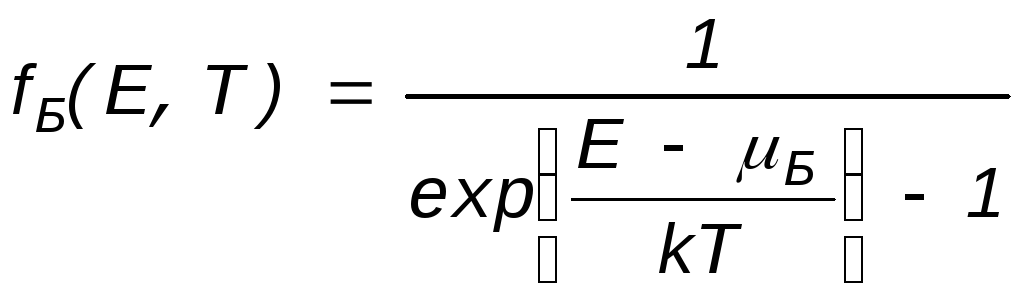
(2.3.)

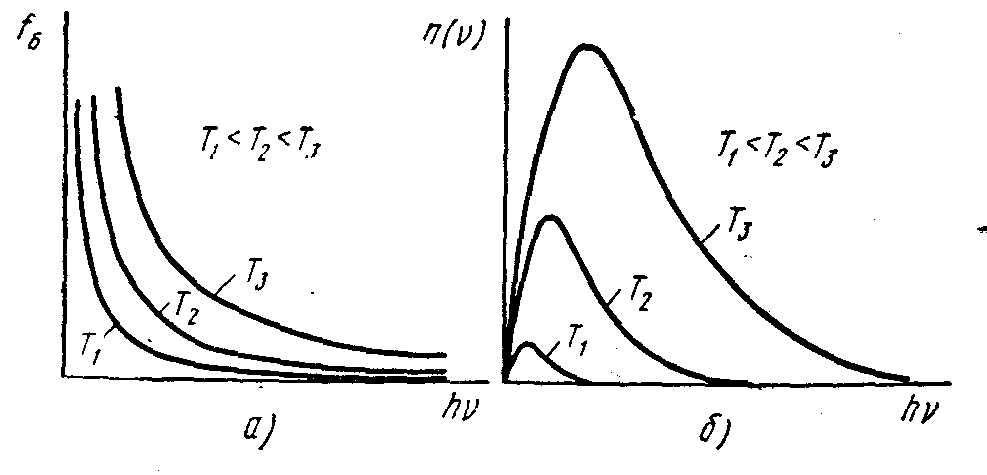
Рис. 2.2. Графики функции распределения Бозе — Эйн­штейна (а) и распределение частиц по энергиям (б) при трех различных значениях температуры

В условиях равновесия бозоны имеют минимум свободной энергии. Поэтому химический потенциал бозонов = 0.

2.3.Функция распределения Ферми—Дирака

Если частицы подчиняются принципу Паули (например, электроны, нейтроны и др.), то в каждом энергетическом состоянии одновременно не может быть более одной частицы. В этих условиях функция распределения, выражающая среднее число частиц в данном энергетическом состоянии, будет представлять собой вероятность заполнения данного состояния. Расчетом наиболее вероятного распределения по энергетическим уровням неразличимых частиц, подчиняющихся принципу Паули, получают формулу ·

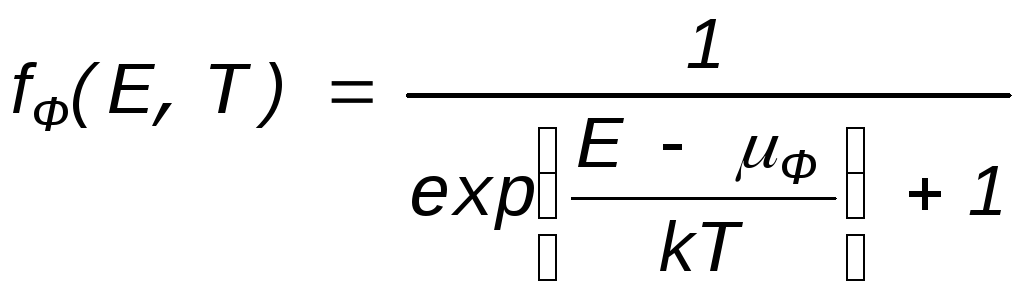(2.4.)

получившую название функции распределения Ферми—Дирака. Частицы, описываемые этой функцией распределения, получили; название фермионов.

Рассмотрим основные свойства распределения Ферми—Дирака применительно к электронам в металле. При температуре абсолютного нуля электроны последовательно занимают все состояния, начиная с самого нижнего, соответствующего дну зоны проводимости. Значение функции распределения для всех этих уровней, очевидно, равняется единице. Как видно из формулы (2.4.),. последним заполненным состоянием будет энергетический уровень, высота которого, отсчитанная от дна зоны проводимости, равна химическому потенциалу Е_F = μ_Ф. Этот энергетический уровень Е_F полу­чил название уровня Ферми. Все энергетические уровни, лежащие выше уровня Ферми, свободны, а значение функции распределения для этих уровней равно нулю (f_Ф(Е>E_F) = 0). Описанное распределе­ние электронов по энергиям при Т = 0°К показано на рис.2.3,а ступенчатой линией.

При повышении температуры часть электронов переходит на более высокие энергетические уровни Е > Е_F, в результате чего вероятность заполнения этих уровней увеличивается, а вероятность заполнения уровней, лежащих ниже уровня Ферми Е <E_F, уменьшается. Ход кривых функции распределения для двух значений температуры, отличных от нуля, показан кривыми на рис. 2.3,а.

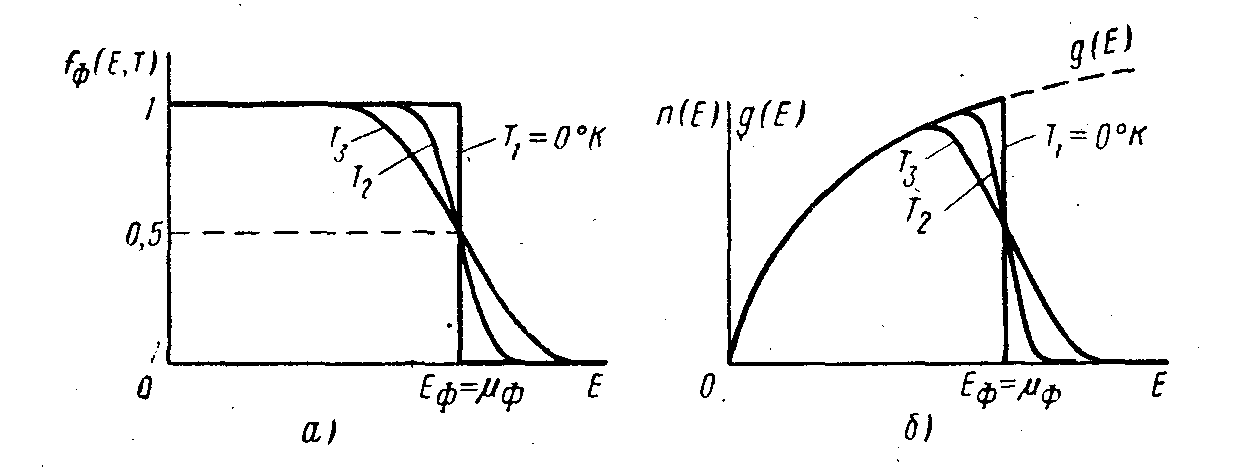
Рис. 2.3. Графики функции распределения Ферми — Дирака (а) и распределение частиц по энергиям (б) при трех различных значениях

температуры

С учетом введенного понятия об уровне Ферми функция распреде­ления Ферми—Дирака запишется так:

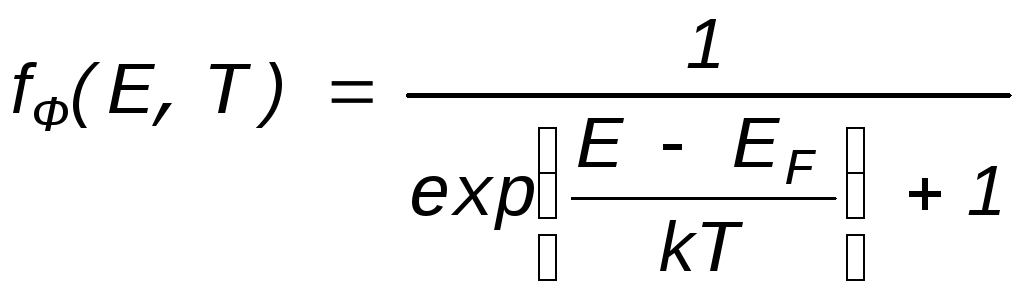(2.5.)

Из формулы (2.5) следует важное свойство уровня Ферми: вероят­ность заполнения электроном уровня E_F при любой температуре равна 1/2.

Графики полученного распределения электронов для трех значений температуры показаны на рис. 2.4,6.