4.4. Векторний добуток векторів. Мішаний добуток.

Задаємо у просторі додатню орієнтацію. Будемо вважати, що трійка векторів орієнтована за правилом правої руки, тобто з кінця третього вектора найменший оберт від першого до другого видно проти годинникової стрілки (рис.4.7),

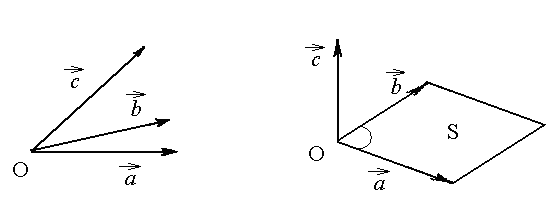
Рис.4.7. Рис.4.8.

Означення. Векторним добутком двох векторів та називають вектор , що задовольняє наступним умовам:

1. Модуль вектора 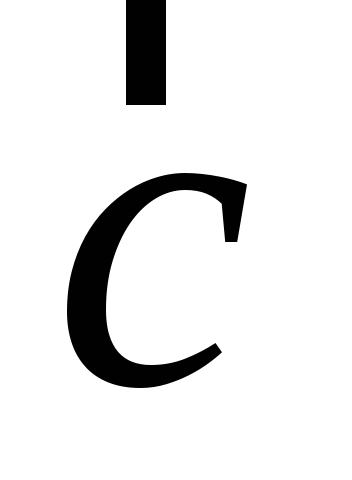чисельно дорівнює площі паралелограма, побудованого на векторах 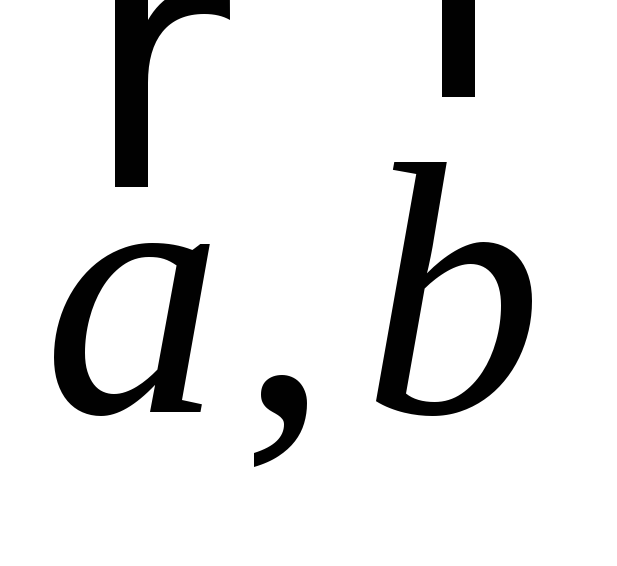,(рис.4.8)

,

де

2. Вектор напрямлений перпендикулярно до площини цього паралелограма, тобто

і .

2. Впорядкована трійка векторів (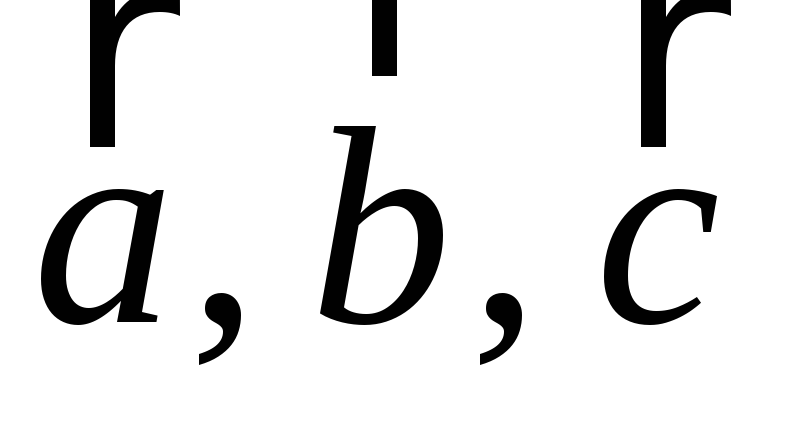) задає додатню орієнтацію простору.

Властивості векторного добутку:

1. При зміні порядку співмножників векторний добуток змінює свій знак на протилежний, модуль при цьому не змінюється.

.

Дійсно при перестановці векторів та площа паралелограма, побудованого на векторах, не змінюється, однак орієнтація векторів і буде лівою.

2. Векторний квадрат дорівнює нуль – вектору, тобто

(за визначенням).

3. Скалярний множник можна виносити за знак векторного добутку, тобто якщо 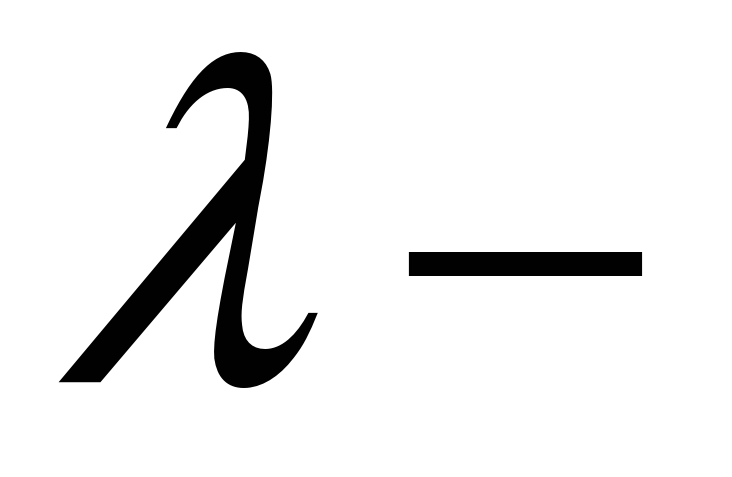скаляр, то

.

4. Для будь-яких трьох векторів 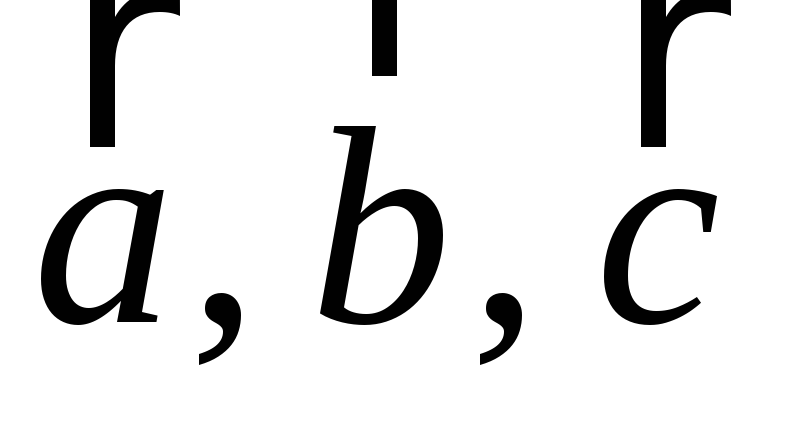справедлива рівність

(розподільна властивість).

Розглянемо координатну форму векторного добутку. Нехай

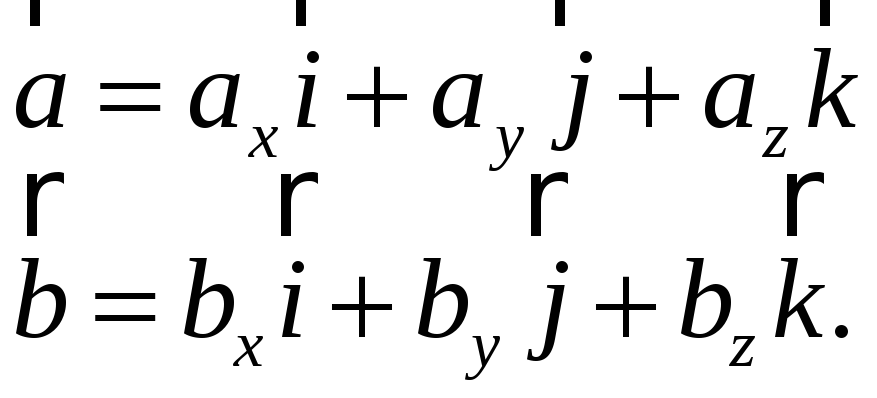
Якщо помножити векторно , одержимо таку рівність

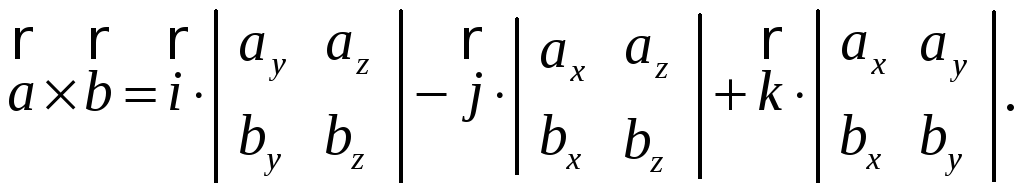
Останню рівність можна записати у вигляді визначника третього порядку

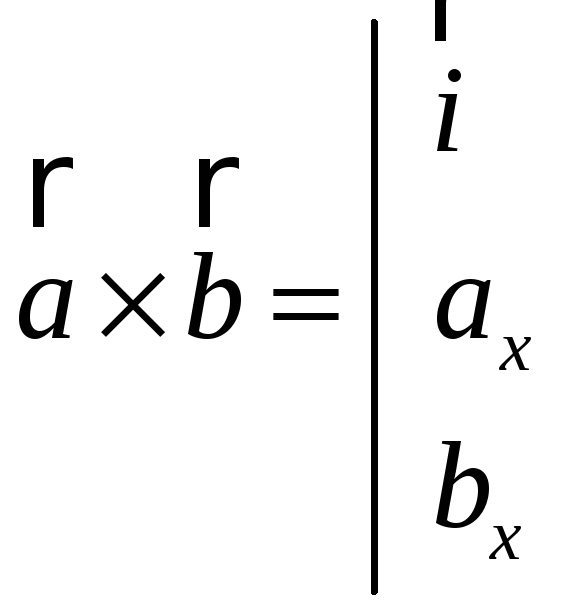
Знайдемо довжину вектора :

.

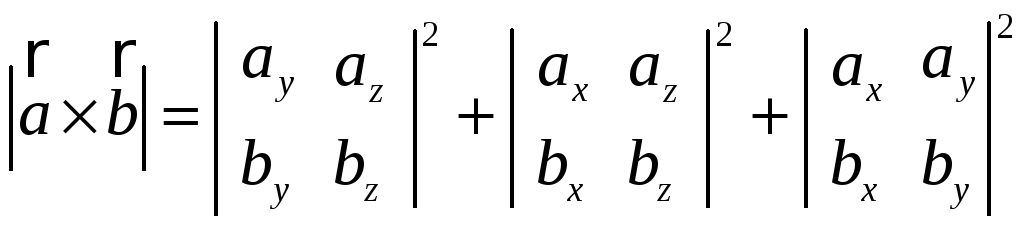Приклад. Знайти площу трикутника з вершинами , і .

Площа трикутника дорівнює площі паралелограма, побудованого на векторах і . і , звідси

=.

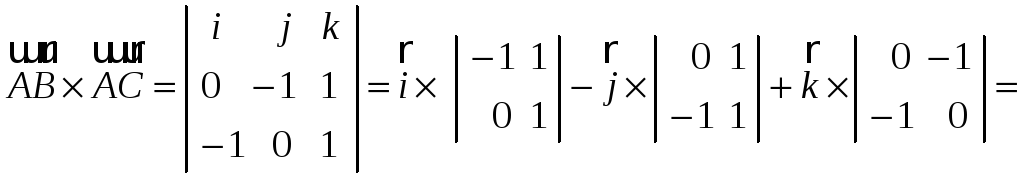
Отже,

.

Означення. Мішаним добутком (або векторно-скалярним добутком) векторів , , називається число

.

Побудуємо паралелепіпед (рис. 4.9), ребрами якого є вектори ,,, що приведені до загальної вершини . Нехай вектор , тобто він перпендикулярний до площини, в якій лежать вектори і (напрям ). Нагадаємо, що – площа паралелограма, побудованого на векторах і , тобто площа основи паралелепіпеда. Висота цього паралелепіпеда H

.

Знак плюс відповідає гострому куту , знак мінус – тупому куту . У першому випадку вектори утворюють праву трійку, а у другому – ліву трійку.

Рис. 4.9

На основі визначення скалярного добутку маємо:

,

де – об’єм паралелепіпеда, побудованого на векторах , , . Звідси

,

тобто мішаний добуток трьох векторів дорівнює об’єму паралелепіпеда, побудованого на цих векторах, який береться із знаком плюс, якщо ці вектори утворюють праву трійку, та з знаком мінус, якщо вони утворюють ліву трійку.

Зазначимо основні властивості мішаного добутку:

1. Мішаний добуток не змінюється при циклічній перестановці цого співмножників, тобто

.

Дійсно у цьому випадку не змінюється об’єм паралелепіпеда та орієнтація його ребер.

2. При перестановці двох сусідніх співмножників мішаний добуток змінює свій знак на протилежний:

,

тобто при перестановці співмножників права трійка переходить у ліву, а ліва у праву. За допомогою мішаного добутку одержимо необхідну та достанню умову компланарності трьох векторів :

(об’єм паралелепіпеда дорівнює нулю).

Якщо

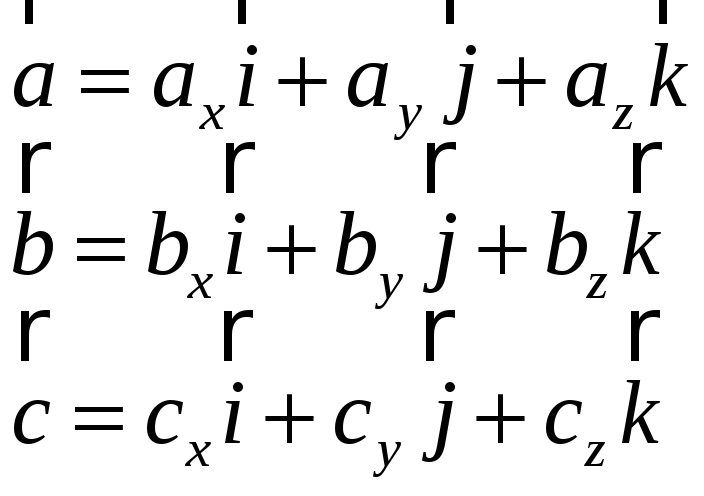
то, використовуючи вирази у координатах для векторного та скалярного добутків, одержимо:

.
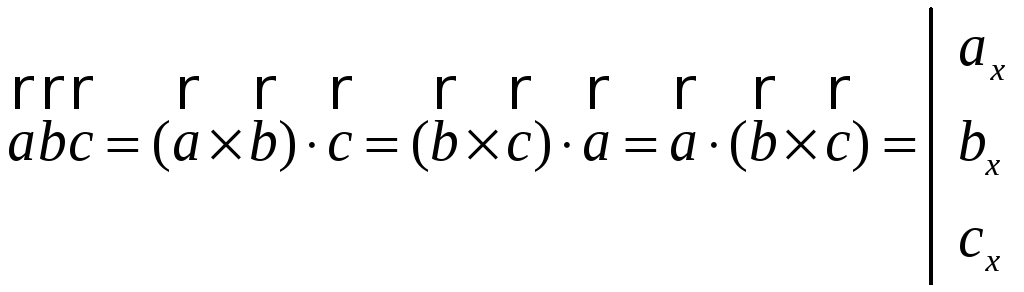