Розділ 2. Векторна алгебра Лекція 4. Вектори та дії над ними. Скалярний, векторний та мішаний добутки векторів.

4.1 Вектори у геометричній формі та дії над ними.

2. Прямокутна система координат. Розкладення вектора по трьох некомпланарних векторах. Дії над векторами, заданими координатами.

3. Скалярний добуток векторів та його властивості

4. Векторний та змішаний добуток векторів.

4.1. Вектори у геометричній формі та дії над ними

Вектором називається напрямлений відрізок. Початок вектора називається точкою його прикладення. Зображується вектор відрізком зі стрілкою, що розташована біля кінця вектора (рис.4.1). Позначається вектор або . Напрямком вектора називається напрямок променя , довжиною (модулем) вектора називається довжина відрізка .

Рис.4.1

Два вектори називаються рівними, коли вони суміщаються паралельним переносом. Рівні вектори мають рівні довжини і однакові напрями. Вектор, у якого початок і кінець співпадають, називається нульовим і позначається через .Сумою кількох векторів, наприклад називається вектор

,

який за величиною та напрямком дорівнює вектору, початком якого є початок вектора (першого доданка), а кінець – кінець вектора (останнього доданка)(рис 4.2)

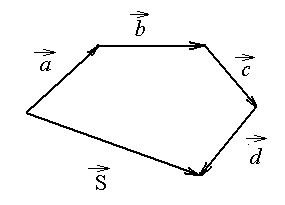
Рис. 4.2

Легко перевірити, що додаток має такі властивості:

1. додаток векторів – переставний

,

2. сполучна властивість

,

3) .

4) .

(Вектор протилежний вектору , його довжина дорівнює довжині вектора , а напрям – протилежний вектору ).

Під різницею векторів та розуміємо вектор

,

такий, що дорівнює сумі векторів та. Добутком вектора на скаляр називається вектор , який має довжину , а напрям такий, як у , якщо , або такий, як у , якщо . Операція множення на число має такі властивості:

1.;

;

2. ;

3. ;

/,

де скаляри; одиничний вектор.

Два вектори та називаються коленіарними, якщо вони належать одній прямій або паралельним прямим. Можна довести, що необхідньою і достатньою умовою колінеарності двох векторів є їх пропорціональність, тобто

скаляр).

Три вектори називаються компланарними, якщо вони належать будь-якій площині або паралельні їй. Можна довести, що три ненульових вектори компланарні тоді та тільки тоді, коли один з них є лінійною комбінацією двох інших, тобто

,

де скаляри.

Розглянемо ще одне визначення, що має дуже важливе значення в теорії векторів. Це визначення проекції вектора на вісь. Нагадаємо, що вісь – це пряма, яка має напрямок. Заданий напрямок будемо вважати додатним, протилежний напрямок – від’ємним.

Під компонентою вектора відносно осі розуміємо вектор , початок якого є проекція на вісь початку вектора , а кінець якого є проекція на вісь кінця цього вектора.

Під проекцією вектора на вісь розуміємо скаляр

,

який дорівнює довжині компоненти вектора на вісь , якщо її напрямок збігається з напрямом осі , та – мінус довжині компоненти, коли її напрямок протилежний напрямку осі. Вкажемо на основні властивості проекції.

1. Проекція вектора на вісь дорівнює добутку довжини вектора на косинус кута між напрямком вектора та напрямком осі, тобто

.

2. Проекція суми додатку будь-якого числа доданків – векторів на дану вісь дорівнює додатку їх проекцій на цю вісь .

3. Якщо даний вектор помножити на скаляр, то його проекцію на івсь теж треба помножити на цей скаляр .