
Timofeeva_S_S_Nadezhnost_tekhnicheskikh_sistem_i_tekhnogenny_risk_uchebn_posobie_Irkutsk_Izd-vo_IRNITU_2015_Ch_1_141
.pdf
0,111871 0,005374 0,048036
0,087884 0,004260 0,048475
0,068907 0,003364 0,048815
0,053947 0,002648 0,049079
0,042185 0,002079 0,049283
0,032958 0,001630 0,049442
0,025731 0,001275 0,049566
0,020078 0,000997 0,496620
Графическая иллюстрация результатов дана на рис. 2 и 3.
Рис. 2. Вероятность безотказной работы
Рис. 3. Интенсивность и плотность Распределения времени до отказа
Согласно (2.7), среднее время безотказной работы системы будет равно:

Пример 2.Требуется определить кратность резервирования системы с постоянным резервом, обеспечивающим вероятность безотказной работы 0,96 в течение времени t =150 час. Элементы системы равнонадежны и имеют экспоненциальное распределение со средним временем безотказной работы Т=300 час. Найти также кратность резервирования для системы, элементы которой имеют распределение Рэлея с тем же средним.
Решение: Кратность резервирования может быть определена по формуле:
где P(t) – вероятность безотказной работы элемента в течение времени t;
Pc(t)=0,96 – вероятность безотказной работы системы в течение времени t.
Для экспоненциальною распределения  , где
, где 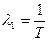 интенсивность отказа элемента..
интенсивность отказа элемента..
Для распределения Рэлея  , где
, где  – параметр распределения.
– параметр распределения.
В течении времени t=150 час получим:
–для экспоненциального закона:
–для закона Рэлея:
Представляя значения Р1(t) и Р2(t) в формулах для кратности резервирования m, получим:
–для экспоненциального распределения:
–для распределения Рэлея:
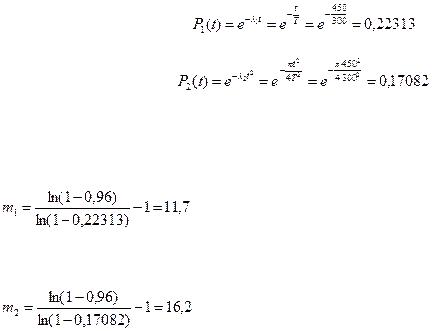
Округляя до целых чисел в большую сторону, получим m1=3, m2=1. Таким образом, для достижения заданной надежности в первом случае потребуется 3 резервных элемента, а во втором случае – только один.
Из примера видно, что надежность системы определяется не только ее структурой и временем работы, но также законом распределения времени до отказа элементов.
Пример 3. В условиях предыдущего примера необходимо обеспечить заданную надежность системы в течении времени t=450 час.
Решение: определим вероятность безотказной работы элемента в течение времени t=450 час для экспоненциального распределения и распределения Рэлея:
Найдем кратность резервирования:
–для экспоненциального распределения:
–для распределения Рэлея:
Округление до целых чисел дает требуемую кратность m1=12, m2=17.Если система работает время t =450 час, то для достижения заданной надежности необходимо иметь 12резервных элементов в первом случае и 17 резервных элементов во втором случае.
Из расчета следует, что структурное резервирование не может обеспечить вероятность безотказной работы системы 0,96 в течение 450 часов. Кратность резервирования настолько высока, что ее практическая реализуемость вряд ли возможна.
Пример 4. Дана резервированная система с постоянным резервом кратности m, все элементы которой равнонадежны и имеют усеченный нормальный закон распределения времени до отказа с параметрами m0 = 400 час и σ0 = 200 час.
Определить все показатели надежности системы. Результаты представить в виде таблиц и графиков. Принять m = 0,1,2.

Решение: для равнонадежных элементов формулы (1)–(3) показателей надежности принимают вид:
Pc(t) = 1– (1–P(t))m+1
fc (t)=(m+1)f(t)(1–P(t)) m
λс(t) =
Плотность распределения времени до отказа и вероятность безотказной работы для усеченного нормального распределения равны соответственно:
f(t) =
P(t) =
где Ф0 (t) – функция Лапласа.
Значения вероятности безотказной работы системы Pc(t) для кратности резервирования m = 0,1,2 содержатся в табл. 2. Соответствующие графики приведены на рис. 4.
Следует иметь в виду, что при больших значениях t вероятность безотказной работы настолько мала, что нет смысла эксплуатировать систему. Таблица необходима только для иллюстрации результатов решения задачи, представления решения в графическом виде и вычисления среднего времени безотказной работы системы методом Симпсона.
Из графиков следует, что Pc(t) возрастает при увеличении кратности резервирования, причем этот эффект тем сильнее, чем меньше m.
На основе данных таблицы 2 приближенно вычислим среднее время безотказной работы системы для значений m = 0,1,2. Воспользуемся формулой Симпсона:
Т1 = 
в которой шаг интегрирования примем равным h = 50 час, n = 20. Расчеты показывают, что при m= 0 Т1 ≈ 411 час, при m = 1 Т1 ≈ 518 час, при m = 2 T1≈573 час.
В табл. 3 содержатся значения плотности распределения вероятностей fc(t) для той же кратности и резервирования. Графики fc(t) приведены на рис. 5.
Пример 5. Дана резервированная система с резервом замещением кратности m = 2. Элементы системы имеют постоянную интенсивность отказа λ = 0,05, час-1. Определить вероятность безотказной работы в среде и время безотказной работы системы. Сравнить Pc(t) с постоянно включенным резервом.
Решение: по формуле (13) получим:
Pc(t) = 
Рассчитанные Pc(t) при различных значениях t сведены в табл. 5. Для сравнения в таблицу помещены также значения P  (t) для постоянно включенного резерва.
(t) для постоянно включенного резерва.
График вероятности безотказной работы для обоих видов резервирования показан на рис. 7.
Среднее время безотказной работы для резерва замещением по формуле(11)
равно T  c=3T
c=3T 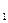 =3∙20=60 час. Для постоянного резерва, как было показано в примере 1, это время составляет 36,7 часа.
=3∙20=60 час. Для постоянного резерва, как было показано в примере 1, это время составляет 36,7 часа.
Порядок выполнения работы
1.Внимательно изучите теоретические положения и примеры расчетов.
2.Выполните расчеты по заданиям, приведенным ниже.
3.Подготовьте отчет.
Задание.1. Техническая система представляет собой дублированную систему с постоянно включенным резервом. Вероятность безотказной работы основной и резервной подсистем в течение t = 200 час равна 0,8. Найти вероятность безотказной работы и вероятность отказа системы в течение времени t. Найти среднее время безотказной работы системы при условии, что ее подсистемы имеют постоянную интенсивность отказа.
Задание 2.Интенсивность отказа элементов системы λ=0,0025 час-1. Требуется определить кратность резервирования системы с постоянно включенным резервом, построенную из этих элементов, которая обеспечивает среднее время безотказной работы системы Тl c=800 час.
Задание 3.Найти показатели надежности резервированной системы с постоянным резервом кратности m=3, элементы которой имеют интенсивности
отказа λ0 = 0,004 час  ,
,  = 0,007 час
= 0,007 час  ,
,  =0,002 час
=0,002 час  ,
,  =0,001 час
=0,001 час  .
.
Время непрерывной работы системы t = 120 час.
Задание 4. Определить показатели надежности мажоритарной системы, состоящей из 6 равнонадежных элементов, время до отказа которых
равномерно распределено на интервале от 0 до 1000 часов. Количество резервных элементов равно 2. Получить аналитическое и графическое представления показателей надежности системы.
Задание 5. Получить формулу для вероятности безотказной работы мажоритарной системы, состоящей из элементов разной надежности при n = 4, m = 2.
Задание 6.Интенсивность отказа одного элемента λ = 0,0035 час  . Требуется определить кратность резервирования системы (резерв замещением), построенную из этих элементов, которая обеспечивает среднее время
. Требуется определить кратность резервирования системы (резерв замещением), построенную из этих элементов, которая обеспечивает среднее время
безотказной работы системы T  =800 час.
=800 час.
Задание 7.Найти показатели надежности P  (t), Тс,
(t), Тс,  (t) резервированной системы (резерв замещением) кратности m =3, элементы которой имеют
(t) резервированной системы (резерв замещением) кратности m =3, элементы которой имеют
интенсивности отказа λ  =0,04 час
=0,04 час  , λ
, λ  = 0,07час
= 0,07час  , λ
, λ  = 0,02 час
= 0,02 час  , λ
, λ  = 0,1 час
= 0,1 час  . Решение получить в виде формул, таблиц и графиков.
. Решение получить в виде формул, таблиц и графиков.
Задание 8. Для резерва замещением кратности m получить формулу вероятности безотказной работы, если элементы системы равнонадежны и
имеют гамма-распределение времени до отказа с параметрами  и
и  .
.
Задание 9. Для резерва замещением кратности m получить формулу плотности распределения времени безотказной работы при условии, что системы равнонадежны и имеют нормальное распределение с параметрами m и  (
(  <m/3).
<m/3).
Задание 10. Даны две системы со скользящим резервом. Первая система состоит из n = 7 элементов, из которых m=3 резервных. Вторая система состоит из n= 5 элементов с m = 2 резервными. Определить более надежную систему по критерию вероятности безотказной работы. Элементы обеих систем имеют
постоянную интенсивность отказа λ =0,01 час  .
.
Задание 11. Дана последовательно-параллельная система размером 3×5 (5 элементов нерезервированной системы, 3 резервных подсистемы) с постоянно включенным резервом. Все элементы имеют одинаковую надежность, время до отказа элементов имеет распределение Рэлея с математическим ожиданием Т = 50 час. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию Pc(t). Указание: воспользоваться формулами (8) и (14).
Задание 12. Дана последовательно-параллельная система размером 3×5 (5 элементов нерезервированной системы, 3 резервных подсистемы), резервированная методом замещения. Все элементы имеют одинаковую
интенсивность отказа λ=0,02 час  . Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию Pc(t). Указание: воспользоваться формулами
. Требуется определить вероятность безотказной работы системы при общем и раздельном резервировании. Провести сравнение по критерию Pc(t). Указание: воспользоваться формулами
(9) и (15).
Задание 13. Элементы резервированной системы с постоянно включенным резервом имеют распределение Вейбулла времени работы до отказа. Найти выражениедля среднего времени безотказной работы системы при кратности резервирования m = 0,1, 2, 3,4, 5. Вычислить среднее время безотказной
работы при параметрах закона распределения 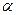 =2,5,
=2,5,  = 20. Решение представить в виде таблицы.
= 20. Решение представить в виде таблицы.
Задание 14. Даны две системы с постоянно включенным резервом с дробной кратностью резервирования m = 1/2 и m = 2/3 соответственно. Определить показатели надежности систем Pc(t), Tc, λc(t). Решение представить в виде формул, графиков и таблиц. Известны следующие исходные данные для числового анализа: время работы системы t= 0÷500 час, среднее время безотказной работы нерезервированной системы Т=550 час, основная и все резервные системы равнонадежны и имеют экспоненциальное распределение времени до отказа.. Определить какая из систем имеет более высокие показатели надежности.
Задание 15.Даны две системы, описанные в задание 14. Определить
критическое время t  , свыше которого резервирование с дробной кратностью не целесообразно. Определить значение вероятности Р(tкр). Решение получить в аналитическом и численном виде.
, свыше которого резервирование с дробной кратностью не целесообразно. Определить значение вероятности Р(tкр). Решение получить в аналитическом и численном виде.
Задание 16. Резервированная система с постоянно включенным резервом состоит из двух подсистем, имеющих различные законы распределения
времени до отказа. Необходимо вычислить Рс(t), T  , λ
, λ  (t). Решение получить в аналитическом виде, в виде графиков и таблиц. Графики представить в диапазоне t = 0÷500 час. Исходные данные содержатся в табл. 6.
(t). Решение получить в аналитическом виде, в виде графиков и таблиц. Графики представить в диапазоне t = 0÷500 час. Исходные данные содержатся в табл. 6.
Таблица 6 - Сводные данные расчетных значений статистических характеристик
№ интер |
Границы |
Середина |
Частота в |
Хср· (Хср– |
(Хср– |
(Хср– |
Час- |
|
вала |
интервала |
интервала Хср |
интер вале ni |
ni |
x) |
x)2 |
2·ni) |
тость, Pi |
….
Последовательность расчетов статистических характеристик:
Составить ряд распределения.
Для упрощения расчета численных значений случайной величины разбиваются на несколько интервалов. При объеме выборки около 100 единиц рекомендуется назначать 6–10 интервалов. Ширина интервала равна
∆X=W/k, (1)

где W = Хтax – Xmjn – размах выборки;
Хтах Хmjn – максимальное и минимальное значения случайной величины в выборке;
к – число интервалов.
В колонку 2 табл. 1 записываются границы интервалов в порядке возрастания случайной величины. т. е. составляется ряд распределения.
1.2. Рассчитать среднее значение выборки 
Для этого в каждом интервале определяется среднее значение интервала, подсчитывается частота ni попадания случайных величин в каждый интервал. При этом если значение попадает вне границы двух интервалов, его нужно отнести к левому интервалу.
Среднее значение выборки определяется по формуле
(2)
где Xcp i – середина i-го интервала;
ni– число случаев в i-том интервале;
 –сумма значений по вертикали в колонке 5;
–сумма значений по вертикали в колонке 5;
N – объем выборки;
к – число интервалов.
Среднее число выборки и является средней наработкой на отказ Т0.
1.3. Определить дисперсию выборки Д и среднее квадратическое отклонение
σ.
Дисперсия случайной величины характеризует ее рассеивание около математического ожидания. Для выборки объемом N дисперсия определяется по формуле
(3)
В соответствии c этой формулой для каждого интервала рассчитываетcя разность и заполняются последовательно колонки 6, 7 и 8 табл. 1. Числитель формулы 2 является суммой всех значений в колонке 8.
Среднее квадратическое отклонение равно корню квадратному из дисперсии,
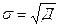 (4)
(4)
Размерность среднего квадратического отклонения совпадает с размерностью случайной величины.
1.4. Рассчитать коэффициент вариации. Числовое значение коэффициента вариации
 . (5)
. (5)
2. Определить закон распределения наработки между отказами
Закон распределения характеризует связь между значениями случайной величины и соответствующими им вероятностями. Случайные величины, используемые для оценки показателей надежности, наиболее часто подчиняются нормальному, экспоненциальному или распределению Вейбулла.
2.1. Построить гистограмму эмпирического распределения и выдвинуть статистическую, гипотезу.
Гистограмма распределения строится по результатам расчета статистической вероятности. Статистической вероятностью является частность
Pi = ni /N, (6)
где ni – число случаев в i-ом интервале;
N – объем выборки.
Значение Р необходимо записать в колонку 9 табл. 1.
При построении гистограммы по оси абсцисс откладываются интервалы (берутся из табл. 1) и на каждом интервале строятся прямоугольники, высота которых равна Р. Масштаб по оси ординат выбирается в зависимости и от максимального значения Р.
По виду гистограммы необходимо выдвинуть статистическую гипотезу, т. е. предварительно определить закон распределения случайной величины. При этом учесть, что если коэффициент вариации V<0,33, то наиболее вероятно нормальное распределение; если К=0,33–2,00, то может быть распределение Вейбулла; если V =1,0, вероятным является экспоненциальное распределение.
2.2. Проверить статистическую гипотезу.
Правдоподобие гипотезы оценивается критериями согласия. С помощью критериев определяется – с какой вероятностью эмпирическое распределение согласуется с теоретическим, т. е. оценивается сходимостью по вероятности.
Наиболее часто применяется критерий Пирсона, который рассчитывается по формуле

(7)
где к, пi, N – см. уравнение 1 и табл. 1;
Pi – теоретическая вероятность в каждом интервале.
Предварительный анализ информации показывает, что распределение между отказами машин во всех вариантах задания близко к экспонентному. В связи с этим в данной работе предлагается оценить сходимость с экспоненциальным законом.
Таблица 2 - Между отказами машин
№ п/п xa xб λ- xa λ- xб е- λ- xa е- λ- xб Рi N · Рi ni-N·Pi (ni-N·Pi)2 
…
Последовательность расчетов
1.Начертить таблицу по форме табл. 2.
2.Заполнить колонки 1, 2, 3, взяв данные из табл. 4–13.
3.Рассчитать показатель, экспоненты
4.Для каждого интервала рассчитать значения Х-ка и X-j, колонки 4 и 5 табл. 2).
5.По табл. 14 X2 значений функции ехр(-λ·х) найти значение в каждом интервале (колонки 6 и 7).
6.Рассчитать теоретическую вероятность Рi в каждом интервале (колонка 8).
7.Определить значение N–Pi для колонки 9. Произведение N·Pi является теоретическим числом случаев попадания изучаемой величины в i-й интервал.
8.Выполнить последующие расчеты и заполнить колонки 10, 11 и 12. Разность (пi – N·Pi) характеризует между опытным и теоретическим числом случаев в каждом интервале.
9.Определить значение критерия X2, суммируя результаты по всем интервалам колонки 12.
10.По критерию X2 и числу степеней свободы
