
- •31. Свойства вероятностей. Условные вероятности.
- •32. Вероятность суммы. Формулы полной вероятности.
- •33. Формула Байеса. Независимые испытания. Схема Бернулли. Формула Бернулли.
- •34. Предельные теоремы в схеме Бернулли.
- •35. Математическое ожидание дискретной случайной величины.
- •36. Дисперсия дискретной случайной величины.
- •37. Непрерывная случайная величина. Интегральная и дифференциальная функция распределения.
- •38. Математическое ожидание и дисперсия непрерывной случайной величины.
- •39. Законы распределения случайных величин.
- •Распределение Пуассона.
- •Геометрический закон распределения.
- •40. Генеральная совокупность и выборка.
37. Непрерывная случайная величина. Интегральная и дифференциальная функция распределения.
Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом.
Пусть X – непрерывная случайная величина с возможными значениями из некоторого интервала (a; b) и x – действительное число. Под выражением X < x понимается событие «случайная величина X приняла значение, меньшее x». Вероятность этого события P(X < x) есть некоторая функция переменной x.
Определение.
Интегральной
функцией распределения
непрерывной случайной величины X
называется функция
![]() ,
равная вероятности того, что X
приняла значение, меньшее x:
,
равная вероятности того, что X
приняла значение, меньшее x:
![]() (1)
(1)
Функция распределения совершенно также определяется для дискретных случайных величин.
Свойства
интегральной функцией распределения
![]() .
.
-
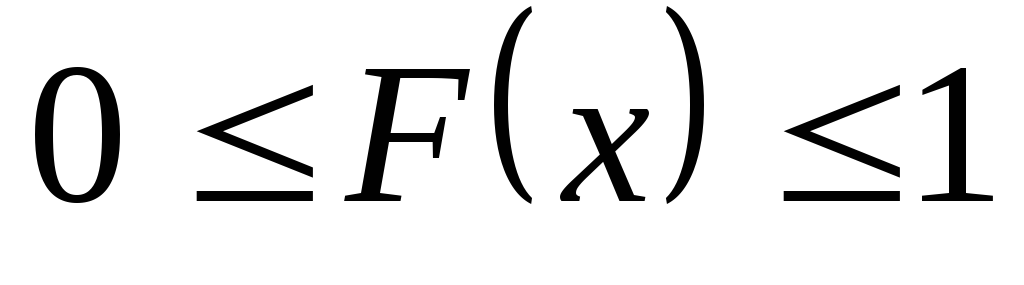 (эта функция есть
вероятность).
(эта функция есть
вероятность). -
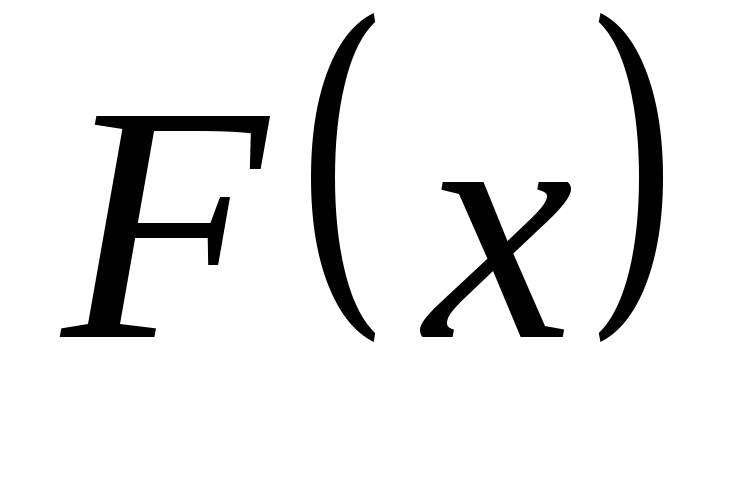 - неубывающая
функция.
- неубывающая
функция. -
Вероятность попадания случайной величины X в полуинтервал
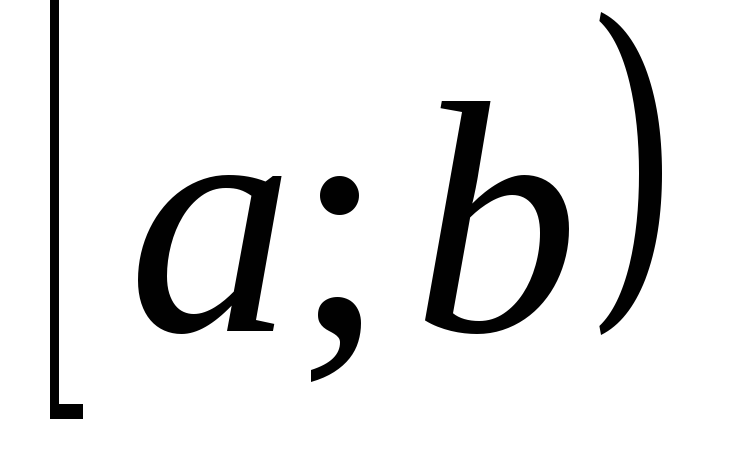 равна разности между значениями функции
распределения в правом и левом концах
интервала (a;
b):
равна разности между значениями функции
распределения в правом и левом концах
интервала (a;
b):
![]()
-
Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:
![]()
-
Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы:
![]()
-
Если возможные значения случайной величины X принадлежат интервалу (a; b), то
-
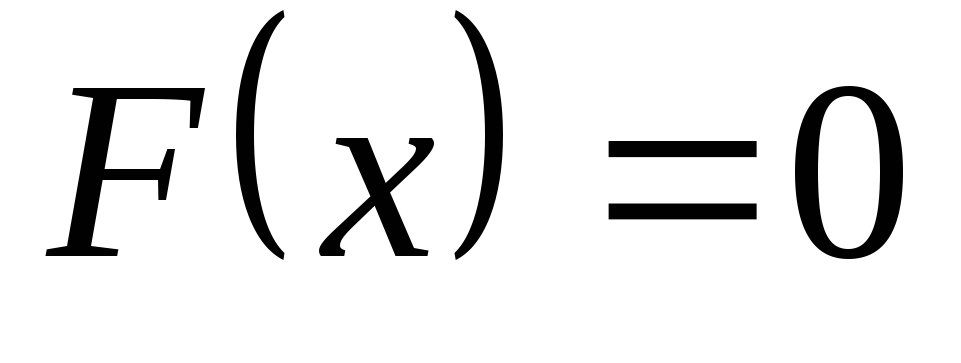 при
при
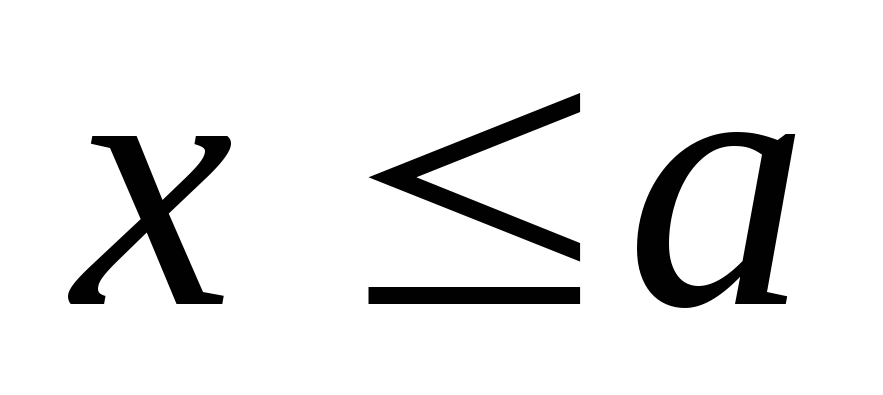 ,
, -
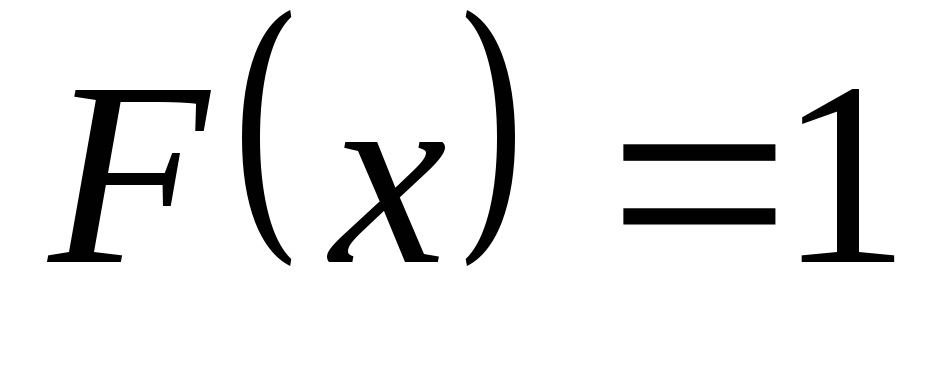 при
при
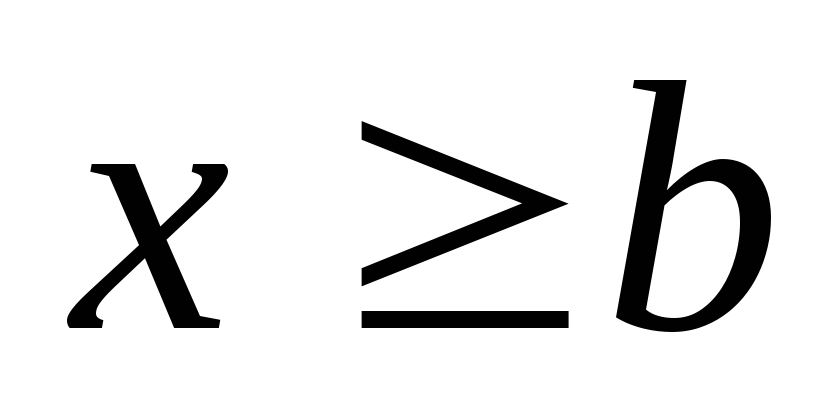 .
.
-
Следствие.
![]() ,
,
![]() .
.
Определение.
Дифференциальной
функцией распределения
непрерывной случайной величины X
называется функция
![]() ,
равная производной интегральной функции:
,
равная производной интегральной функции:
![]() (2)
(2)
Так как
![]() - неубывающая функция, то
- неубывающая функция, то
![]() .
.
Теорема. Вероятность попадания непрерывной случайной величины X в интервале (a; b) равна определенному интегралу от дифференциальной функции распределения величины X, взятому в пределах от a до b:
![]() (3)
(3)
Из (3) следует, что
геометрически вероятность
![]() представляет собой площадь криволинейной
трапеции, ограниченной графиком плотности
вероятности
представляет собой площадь криволинейной
трапеции, ограниченной графиком плотности
вероятности
![]() и отрезками прямых y
= 0, x = a,
x = b.
и отрезками прямых y
= 0, x = a,
x = b.
Следствие.
В частности, если
![]() - четная функция и концы интервала
симметричны относительно начала
координат, то
- четная функция и концы интервала
симметричны относительно начала
координат, то
![]()
На основании
формулы Ньютона-Лейбница можно записать
![]() ,
откуда, в силу следствия 1, можно записать:
,
откуда, в силу следствия 1, можно записать:
![]() (4).
(4).
Верно также
равенство:
![]() (5).
(5).
Пример. Задана плотность вероятности случайной величины X
![]()
![]() .
.
Требуется найти коэффициент A, функцию распределения F(x) и вероятность попадания случайной величины X в интервал (0; 1).
Коэффициент A найдем, воспользовавшись соотношением (5).
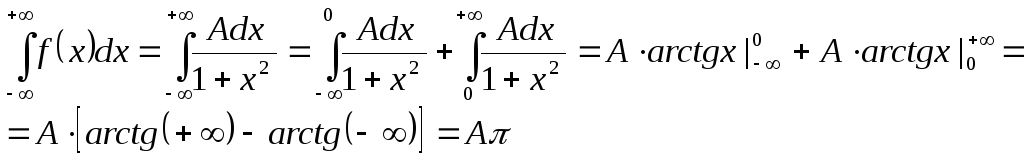
Так как
![]() ,
откуда
,
откуда
![]() .
.
Применяя формулу
(4), получаем функцию распределения
![]() .
.
![]()
Наконец, на основании 3 и 5 свойств, с учетом найденной функции F(x) получим
![]() .
.
38. Математическое ожидание и дисперсия непрерывной случайной величины.
Определение.
Математическим
ожиданием непрерывной случайной величины
X
с плотностью
вероятности
![]() называют величину несобственного
интеграла (если он сходится):
называют величину несобственного
интеграла (если он сходится):
![]() (1)
(1)
Свойства математического ожидания непрерывной случайной величины.
-
Математическое ожидание постоянной величины C равно этой величине.
-
Постоянный множитель можно выносить за знак математического ожидания, т.е.
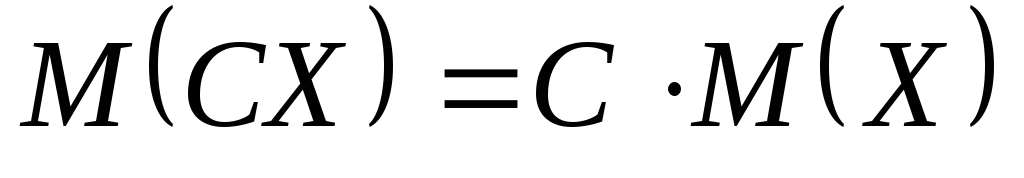 .
. -
Математическое ожидание суммы двух случайных величин X и Y равно сумме их математических ожиданий: M(X+Y) = M(X) + M(Y).
-
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M(X) M(Y).
-
Математическое ожидание разности – двух случайных величин X и Y равно разности их математических ожиданий: M(X–Y) = M(X) – M(Y).
Определение.
Дисперсией
непрерывной случайной величины X,
математическим ожиданием которой
![]() и функция
и функция
![]() является ее плотностью вероятности,
называется величина несобственного
интеграла (если он сходится):
является ее плотностью вероятности,
называется величина несобственного
интеграла (если он сходится):
![]() (2)
(2)
Математическое ожидание и дисперсия непрерывной случайной величины имеют те же свойства, что и математическое ожидание и дисперсия дискретной случайной величины.
Для непрерывной
случайной величины X
среднее квадратическое отклонение
![]() определяется, как и для дискретной
величины, формулой
определяется, как и для дискретной
величины, формулой
![]() .
.
Свойства дисперсии дискретной случайной величины.
-
Дисперсия дискретной случайной величины X равна разности между математическим ожиданием квадрата величины X и квадратом ее математического ожидания:
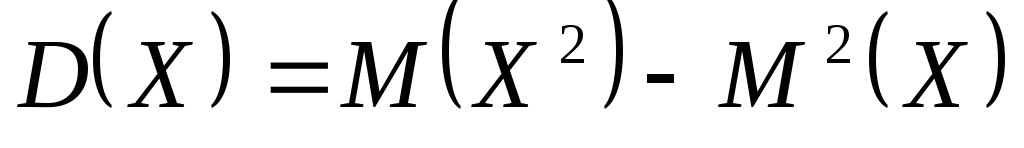
-
Дисперсия постоянной величины равна нулю.
-
Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат:
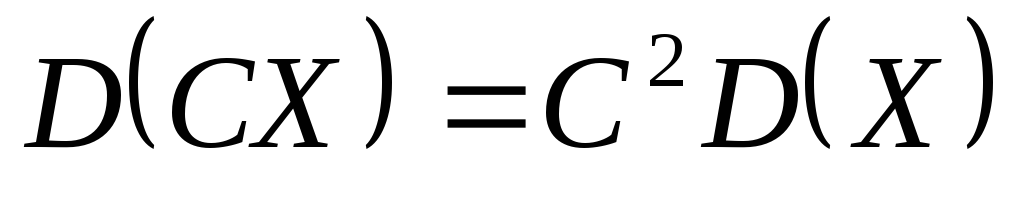
-
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

-
Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин:
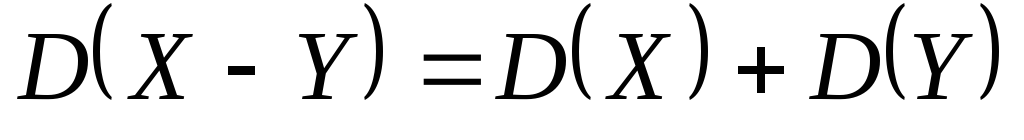
Пример. Случайная величина X задана плотностью вероятности. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение величины X.
![]()
 ,
,
![]()
![]()
