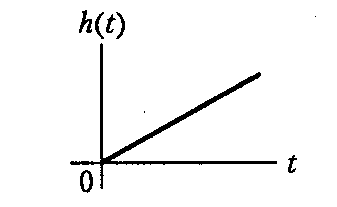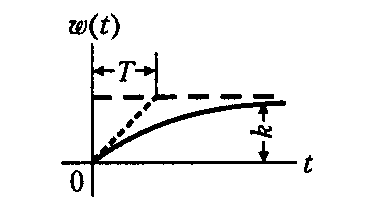- •Основы теории автоматического управления Конспект лекций
- •Терминология
- •Введение
- •1. Классификация систем автоматического регулирования
- •1.1. Классификация по основному признаку
- •1.2. Общая классификация систем автоматического управления
- •2. Математические модели элементов и систем управления
- •2.1. Передаточные функции. Преобразования Лапласа
- •2.2. Типовых звенья и их передаточные функции
- •2.2.1. Усилительное (безынерционное) звено
- •2.2.2. Интегрирующие звенья
- •1. Идеальное интегрирующее звено
- •2. Интегрирующее звено с замедлением
- •3. Изодромное звено
- •2.2.3. Дифференцирующие звенья
- •1. Идеальное дифференцирующее звено
- •2. Дифференцирующее звено с замедлением
- •2.2.4. Инерционное звено первого порядка (апериодическое)
- •2.2.5. Интегро-дифференцирующее звено
- •2.2.6. Инерционное звено второго порядка
- •2.2.7. Запаздывающее звено
- •2.2.8. Представление реальных аср типовыми звеньями
- •3. Основные характеристики звеньев и систем
- •3.1. Статические свойства элементов и систем
- •3.2. Соединения статических элементов
- •3.3. Временные характеристики
- •3.4. Частотные характеристики
- •3.5. Частотные характеристики типовых звеньев
- •1. Частотная характеристика усилительного звена (безынерционного)
- •2. Частотные характеристики инерционного звена первого порядка
- •3. Частотные характеристики интегрирующего звена
- •4. Дифференцирующее звено
- •5. Инерционное звено второго порядка
- •6. Колебательное звено
- •7. Запаздывающее звено
- •8. Частотные характеристики интегро-дифференцирующих звеньев и их соединений
- •3.6. Соединение звеньев. Передаточные функции соединений
- •1. Последовательное соединение звеньев
- •2. Параллельное соединение звеньев
- •3. Встречно-параллельное соединение звеньев или соединение с обратной связью
- •4. Эквивалентные преобразования структурных схем
- •3. Пропорцилнально-интегральные регуляторы
- •4. Пропорционально-интегрально-дифференциольные регуляторы
- •3.8. Последовательные и параллельные корректирующие устройства
- •3.9 Передаточные функции систем автоматического регулирования
- •4. Импульсные системы
- •4.1. Математическое описание дискретных объектов управления в электромеханических системах
- •4.2. Общие сведения об импульсных системах
- •4.3. Цифровые регуляторы в электромеханических системах
- •4.3.1. Методика синтеза регуляторов в мехатронной системе
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Постановка задачи исследования устойчивости
- •5.2. Оценка устойчивости разомкнутой и замкнутой системы с помощью алгебраического критерия Рауса-Гурвица
- •5.3. Частотные критерии устойчивости
- •1. Критерий Михайлова
- •2. Критерий устойчивости Найквиста
- •Приложения
- •Список литературы
- •Оглавление
3. Изодромное звено
Звено записывается уравнением
![]() (2.18)
(2.18)
Передаточная функция звена
![]() ,
,
где
![]() – постоянная времени изодромного
звена.
– постоянная времени изодромного
звена.
Из этих выражений
видно, что звено можно представить в
виде совокупности двух звеньев,
действующих параллельно, идеального
интегрирующего с коэффициентом передачи
![]() и безынерционного с коэффициентом
передачи
и безынерционного с коэффициентом
передачи
![]() .
.
Примеры изодромных звеньев изображены на рис. 2.6
Таким звеном может
быть комбинация пружины с демпфером
(рис. 2.6, б). В качестве входной величины
здесь рассматривается прикладываемая
сила
![]() ,
а в качестве выходной – перемещение
,
а в качестве выходной – перемещение
![]() точки
точки
![]() ,
в которой приложена сила. Это перемещение
складывается из деформации пружины
,
в которой приложена сила. Это перемещение
складывается из деформации пружины
![]() и перемещения поршня
и перемещения поршня
![]() ,
где
,
где
![]() – жесткость пружины;
– жесткость пружины;
![]() – коэффициент скоростного сопротивления
демпфера.
– коэффициент скоростного сопротивления
демпфера.
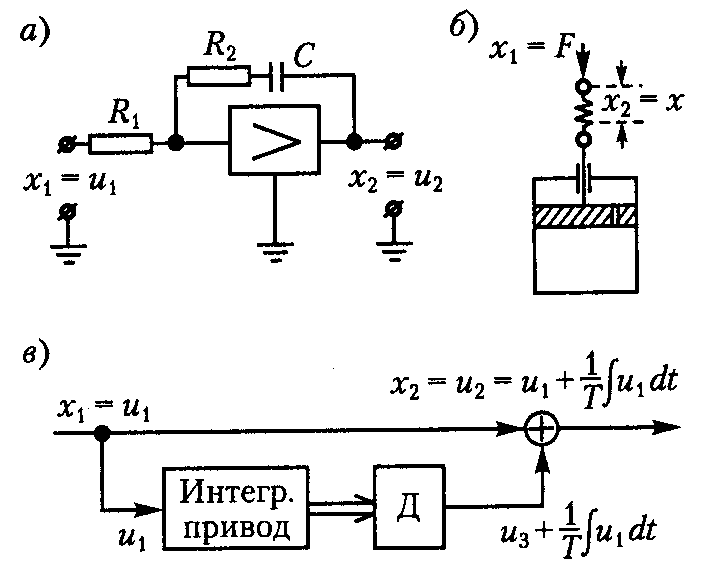
Рис. 2.6. Примеры изодромных звеньев
Результирующее перемещение точки
![]() .
.
При использовании
операционного усилителя (рис. 2.6, а)
изодромное звено может быть получено
посредством применения
![]() – цепи в обратной связи.
– цепи в обратной связи.
В системах
управления часто находят применение
изодромные звенья, построенные на базе
интегрирующего привода (2.6, в). В этом
случае входное напряжение
![]() поступает непосредственно на выход,
кроме того, это же напряжение поступает
на вход интегрирующего привода. Угол
поворота вала интегрирующего привода,
в соответствии с изложенным выше,
пропорционален интегралу от входного
напряжения
поступает непосредственно на выход,
кроме того, это же напряжение поступает
на вход интегрирующего привода. Угол
поворота вала интегрирующего привода,
в соответствии с изложенным выше,
пропорционален интегралу от входного
напряжения
![]() .
На выходном валу устанавливается
какой-либо датчик (Д), представляющий
собой линейный преобразователь угла
поворота в напряжение, например,
потенциометр или линейный вращающийся
трансформатор. Напряжение этого
преобразователя
.
На выходном валу устанавливается
какой-либо датчик (Д), представляющий
собой линейный преобразователь угла
поворота в напряжение, например,
потенциометр или линейный вращающийся
трансформатор. Напряжение этого
преобразователя
![]() суммируется с напряжением
суммируется с напряжением
![]() .
Эта сумма и представляет собой выходное
напряжение
.
Эта сумма и представляет собой выходное
напряжение
![]() .
.
Логарифмическая амплитудно-частотная характеристика (ЛАХ) строится по выражению:
![]() .
.
Асимптотическая
ЛАХ представляет собой две прямые: с
отрицательным наклоном -20 дБ/дек (при
![]() )
и параллельную оси частот (при
)
и параллельную оси частот (при
![]() ).
Из рассмотрения ЛАХ и ЛЧХ видно, что в
области малых частот (меньших, чем
сопрягающая частота) звено ведет себя
как идеальное интегрирующее и тем
точнее, чем меньше частота.
).
Из рассмотрения ЛАХ и ЛЧХ видно, что в
области малых частот (меньших, чем
сопрягающая частота) звено ведет себя
как идеальное интегрирующее и тем
точнее, чем меньше частота.
В области больших
частот (больших, чем сопрягающая частота)
звено ведет себя как безынерционное с
коэффициентом передачи
![]() .
.
Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систем автоматического регулирования.
Временные характеристики интегрирующих звеньев представлены в таблице 2.1, а частотные – в приложении 2.
Таблица 2.1. Временные характиристики интегрирующих звеньев
|
Тип звена и передаточная функция |
Переходная функция |
Функция веса |
|
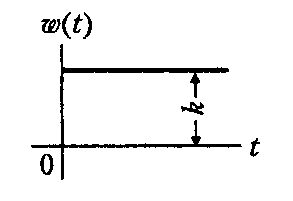
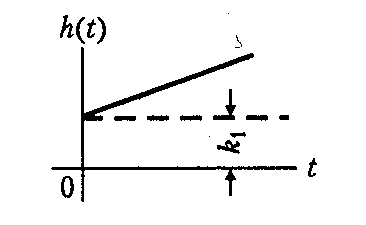
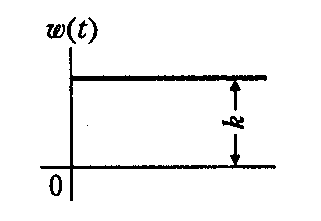
Идеальное
|
h(t) = kt ∙ 1(t) |
w(t) = k ∙ 1(t) |
|
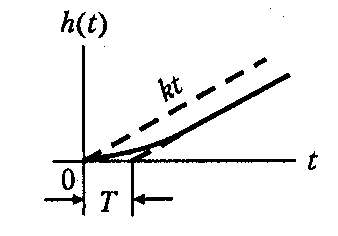
С замедлением
|
|
|
Продолжение табл. 2.1
|
Тип звена и передаточная функция |
Переходная функция |
Функция веса |
|
Изодромное
|
|
|