3. Встречно-параллельное соединение звеньев или соединение с обратной связью
При встречно-параллельном
соединении звеньев на вход звена
одновременно с входной величиной
системы подается ее выходная величина,
прошедшая через звено обратной связи
с передаточной функцией
.
На рис. 3.34
представлена система из звеньев,
соединенных встречно-параллельно. Как
видно из схемы:
.
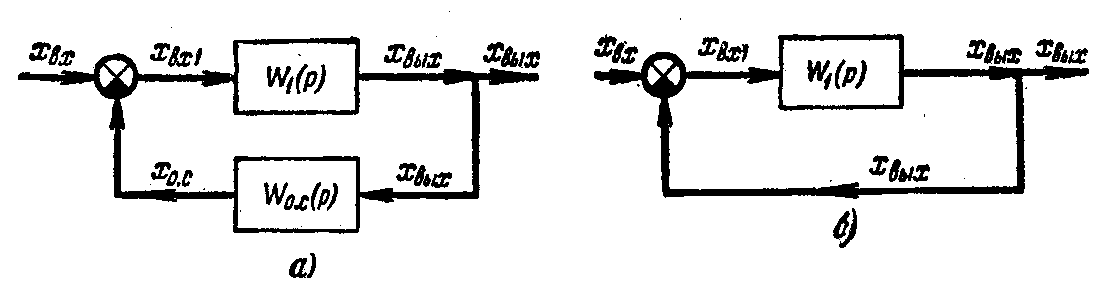
Рис. 3.34. Встречно-параллельное соединение звеньев
При отрицательной, наиболее распространенной обратной связи ее величина вычитается из входной величины. При положительной обратной связи ее величина суммируется с входной величиной.
Передаточная функция системы в этом случае запишется как
.
Разделив это
равенство на
и
учитывая, что
,
а передаточная функция системы
,
получим:
,
откуда
. (3.44)
В знаменателе
знак «+» относится к отрицательной
обратной связи, когда
.
В системах регулирования для обеспечения устойчивости их работы обычно применяется отрицательная обратная связь, тогда выражение (3.44) запишем:
.
На схемах принято в случае наличия отрицательной обратной связи зачернять тот сектор суммирующего устройства, к которому подводится линия, изображающая канал обратной связи (рис. 3.34).
Если выход системы
подать в качестве отрицательной обратной
связи, не пропуская ни через какое
звено, прямо на вход системы (рис. 3.34,
б),
то
.
Следовательно, для этого случая передаточная функция системы будет равна:
. (3.45)
Если в качестве звена обратной связи применяется усилительное звено, то такая связь называется жесткой обратной связью. Система, показанная на рис. 3.34, б является частным случаем жесткой отрицательной обратной связи с коэффициентом передачи усилительного звена, равным единице.
В качестве примера
рассмотрим систему, состоящую из
интегрирующего звена с передаточной
функцией
,
охваченного жесткой отрицательной
обратной связью, для которой
.
Согласно выражению (3.45) передаточная функция системы с ООС будет равна:
,
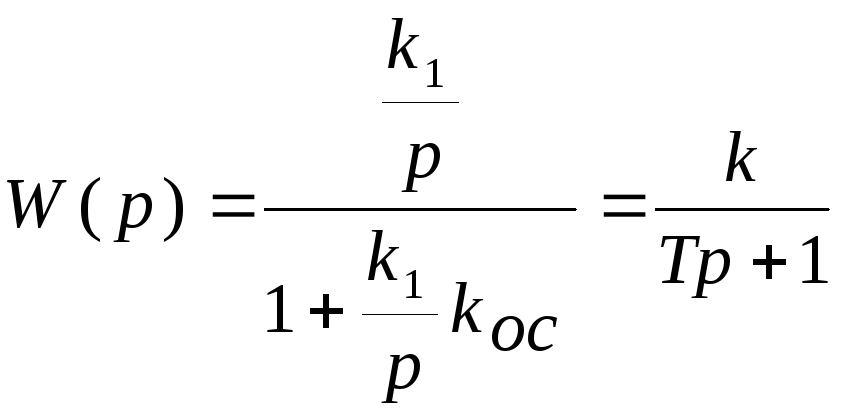где
.
Таким образом, при охвате интегрирующего звена жесткой отрицательной обратной связью в виде усилительного звена получаем инерционное звено первого порядка.
В случае охвата
такой жесткой отрицательной обратной
связью инерционного звена первого
порядка, для которого
,
находим
,
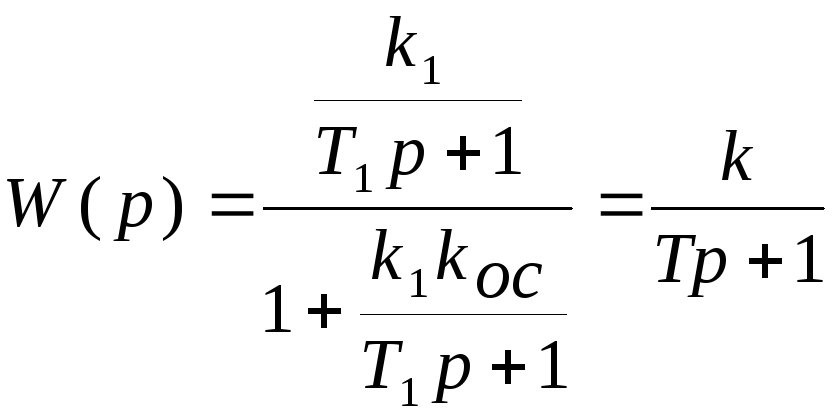где
.
Получаем также
инерционное звено первого порядка, но
коэффициент усиления и постоянная
времени звена при этом уменьшается в
(
)
раз.
4. Эквивалентные преобразования структурных схем
Разбивка дифференциального уравнения
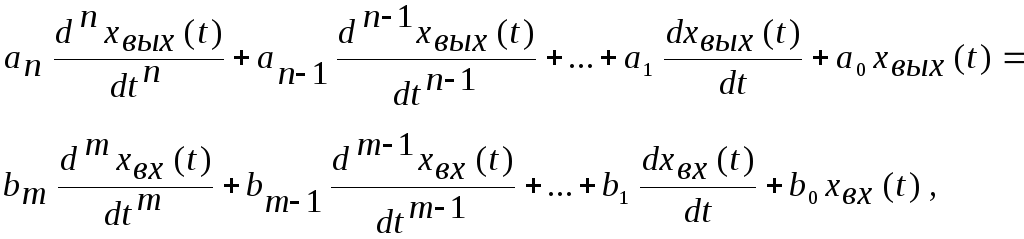
определяющего процесс автоматического регулирования в системе, на дифференциальные уравнения элементарных звеньев, в общем случае может быть выполнена различным образом.
Следовательно, один и тот же процесс автоматического регулирования может быть осуществлен с помощью систем, реализованных различным числом элементарных звеньев с различными структурными связями между ними.
Имея в качестве исходной какую-либо одну из таких систем и определив передаточные функции всех ее элементарных звеньев, можно в дальнейшем упростить структурную схему системы путем ее эквивалентных преобразований. Во всех различных структурных схемах, полученных в результате эквивалентных преобразований первоначальной схемы, передаточная функция системы в целом не изменяется независимо от того, на сколько и каких элементарных звеньев разбита система и какие структурные связи имеются между ее звеньями.
Основные правила эквивалентного преобразования структурных схем следующие:
1. Звенья, соединенные последовательно, могут быть заменены одним звеном с передаточной функцией, равной произведению передаточных функций последовательно соединенных звеньев.
2. Звенья, соединенные параллельно, могут быть заменены одним звеном с передаточной функцией параллельно соединенных звеньев.
3. Звенья, соединенные встречно-параллельно, могут быть заменены одним звеном с передаточной функцией, определяемой по формуле встречно-параллельного соединения
4. Внешнее воздействие
,
приложенное к выходу звена
(рис. 3.40,
а)
с передаточной функцией
,
можно перенести на его вход (рис. 3.40,
б),
поместив между воздействием и входом
звена дополнительное звено с передаточной
функцией
.
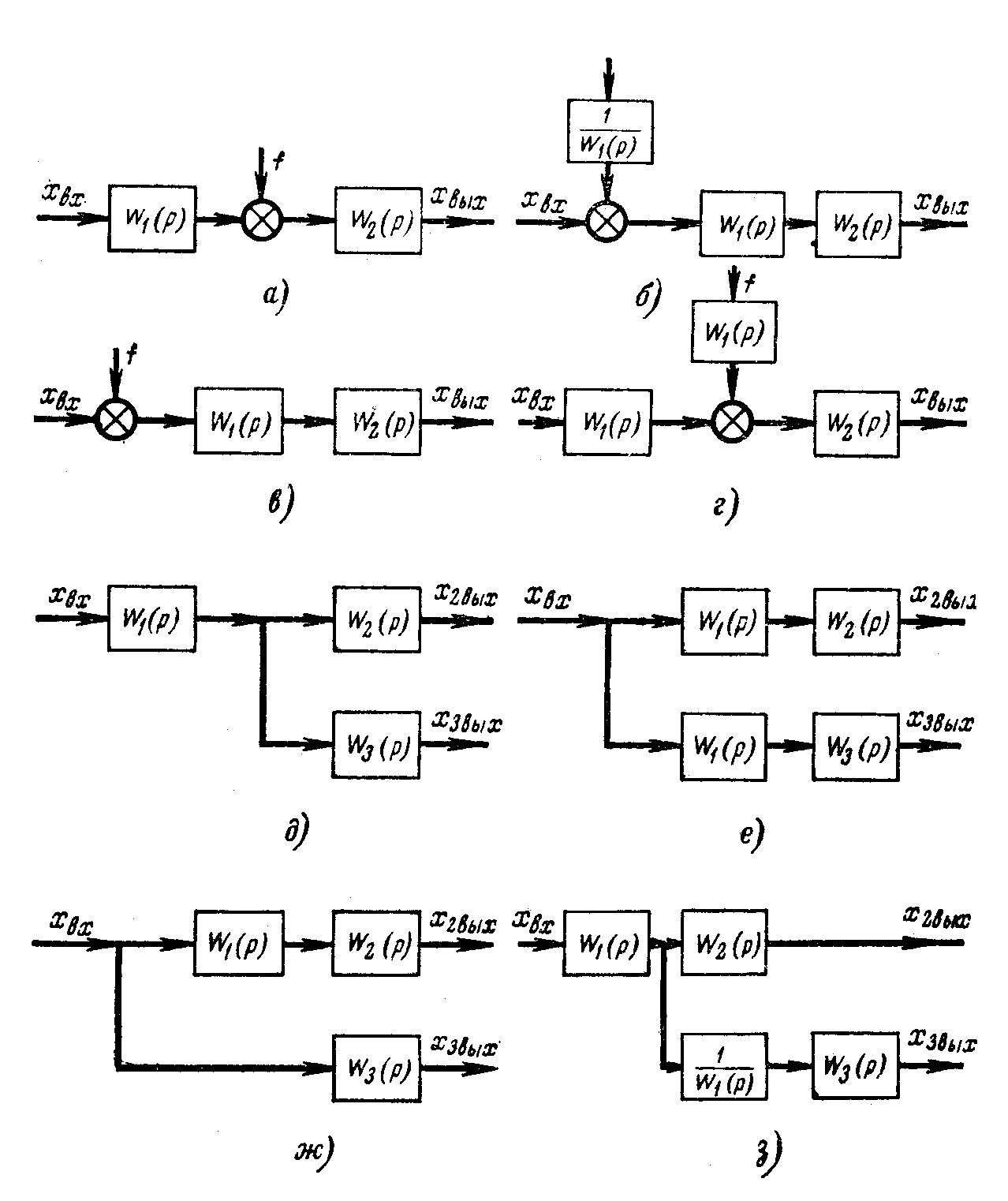
Рис. 3.35. Эквивалентные преобразования структурных схем
5. Внешнее воздействие
,
приложенное к входу звена
(рис. 3.35,
в)
с передаточной функцией
,
можно перенести на его выход (рис. 3.35,
г),
поместив между воздействием и выходом
звена дополнительное звено с той же
передаточной функцией
.
6. Точку присоединения
любой структурной связи к выходу звена,
имеющего передаточную функцию
(рис. 3.35, д),
можно перенести на его вход, включив в
эту связь дополнительное звено с той
же передаточной функцией
(рис. 3.35, е).
7. Точку присоединения
любой структурной связи к входу звена
с передаточной функцией
(рис. 3.35, ж),
можно перенести на его выход, включив
в эту связь дополнительное звено с той
же передаточной функцией
(рис. 3.35, з).
С помощью перечисленных правил структурные схемы с перекрестными связями можно преобразовать в структурные схемы без перекрестных связей, заменять многоконтурные системы автоматического регулирования одноконтурными, а также выделять линейную часть в нелинейных системах автоматического регулирования.
3.7 Типовые передаточные функции
автоматических регуляторов
Автоматические регуляторы по своим динамическим свойствам подразделяются на линейные и нелинейные. При проектировании наиболее часто применяемых линейных автоматических регуляторов используют пропорциональный, интегральный, пропорционально-интегральный и пропорционально-интегрально-дифференциольный законы регулирования.
1. Пропорциональные регуляторы
Пропорциональные регуляторы (П-регуляторы) воздействуют на регулирующий орган пропорционально отклонению регулируемой величины от заданного значения:
Передаточная функция этого регулятора выразится как
Коэффициент
называется коэффициентом передачи
регулятора. В динамическом отношении
П-регуляторы аналогичны усилительному
звену (см. рис. выше).
2. Интегральные регуляторы
Интегральные регуляторы (И-регуляторы) воздействуют на регулирующий орган пропорционально интегралу от отклонения регулируемой величины:
Передаточная функция И-регулятора запишется как
где
– коэффициент передачи регулятора.
Иначе
Следовательно, в И-регуляторе скорость перемещения исполнительного механизма (скорость воздействия на регулирующий орган) пропорциональна отклонению регулируемой величины. В динамическом отношении И-регуляторы представляют собой интегрирующее звено (см. рис. выше).