
- •Основы теории автоматического управления Конспект лекций
- •Терминология
- •Введение
- •1. Классификация систем автоматического регулирования
- •1.1. Классификация по основному признаку
- •1.2. Общая классификация систем автоматического управления
- •2. Математические модели элементов и систем управления
- •2.1. Передаточные функции. Преобразования Лапласа
- •2.2. Типовых звенья и их передаточные функции
- •2.2.1. Усилительное (безынерционное) звено
- •2.2.2. Интегрирующие звенья
- •1. Идеальное интегрирующее звено
- •2. Интегрирующее звено с замедлением
- •3. Изодромное звено
- •2.2.3. Дифференцирующие звенья
- •1. Идеальное дифференцирующее звено
- •2. Дифференцирующее звено с замедлением
- •2.2.4. Инерционное звено первого порядка (апериодическое)
- •2.2.5. Интегро-дифференцирующее звено
- •2.2.6. Инерционное звено второго порядка
- •2.2.7. Запаздывающее звено
- •2.2.8. Представление реальных аср типовыми звеньями
- •3. Основные характеристики звеньев и систем
- •3.1. Статические свойства элементов и систем
- •3.2. Соединения статических элементов
- •3.3. Временные характеристики
- •3.4. Частотные характеристики
- •3.5. Частотные характеристики типовых звеньев
- •1. Частотная характеристика усилительного звена (безынерционного)
- •2. Частотные характеристики инерционного звена первого порядка
- •3. Частотные характеристики интегрирующего звена
- •4. Дифференцирующее звено
- •5. Инерционное звено второго порядка
- •6. Колебательное звено
- •7. Запаздывающее звено
- •8. Частотные характеристики интегро-дифференцирующих звеньев и их соединений
- •3.6. Соединение звеньев. Передаточные функции соединений
- •1. Последовательное соединение звеньев
- •2. Параллельное соединение звеньев
- •3. Встречно-параллельное соединение звеньев или соединение с обратной связью
- •4. Эквивалентные преобразования структурных схем
- •3. Пропорцилнально-интегральные регуляторы
- •4. Пропорционально-интегрально-дифференциольные регуляторы
- •3.8. Последовательные и параллельные корректирующие устройства
- •3.9 Передаточные функции систем автоматического регулирования
- •4. Импульсные системы
- •4.1. Математическое описание дискретных объектов управления в электромеханических системах
- •4.2. Общие сведения об импульсных системах
- •4.3. Цифровые регуляторы в электромеханических системах
- •4.3.1. Методика синтеза регуляторов в мехатронной системе
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Постановка задачи исследования устойчивости
- •5.2. Оценка устойчивости разомкнутой и замкнутой системы с помощью алгебраического критерия Рауса-Гурвица
- •5.3. Частотные критерии устойчивости
- •1. Критерий Михайлова
- •2. Критерий устойчивости Найквиста
- •Приложения
- •Список литературы
- •Оглавление
8. Частотные характеристики интегро-дифференцирующих звеньев и их соединений
В соответствии с
передаточной функцией звена
![]() находим его амплитудно-фазовую
характеристику:
находим его амплитудно-фазовую
характеристику:
![]() . (3.34)
. (3.34)
Вещественная и мнимая частотные характеристики
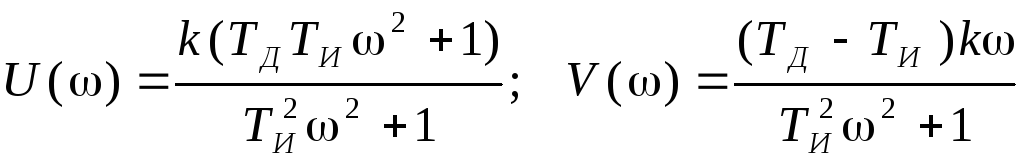 . (3.35)
. (3.35)
Амплитудно-частотная и фазо-частотная характеристика звена имеют вид:
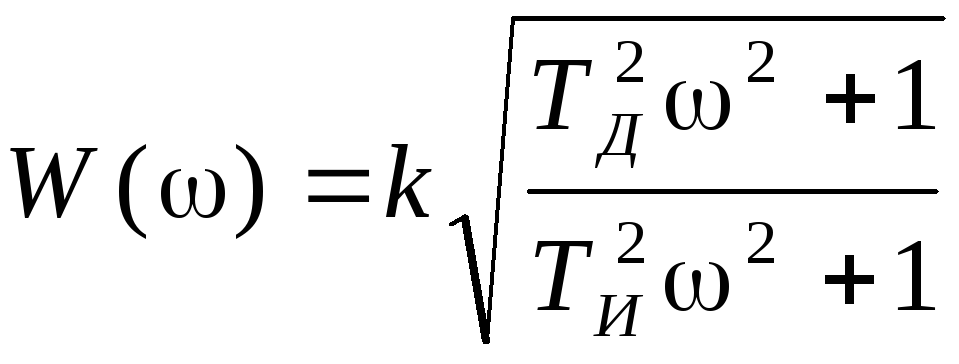 . (3.36)
. (3.36)
![]() . (3.37)
. (3.37)
Амплитудно-фазовую
характеристику можно представить также
в виде явной функции (параметрически
заданной)
![]() ,
используя равенства (3.54).
,
используя равенства (3.54).
Без вывода приводим АФХ интегро-дифференцирующего звена:
![]() , (3.38)
, (3.38)
где
![]() .
.
Следовательно,
АФХ имеет вид окружности, центр которой
расположен на вещественной положительной
полуоси в точке с координатами (![]() ).
Радиус окружности равен
).
Радиус окружности равен
![]() .
.
Амплитудно-фазовые
характеристики для двух различных
соотношений постоянных времени
![]() и
и
![]() представлены на рис. 3.28).
представлены на рис. 3.28).
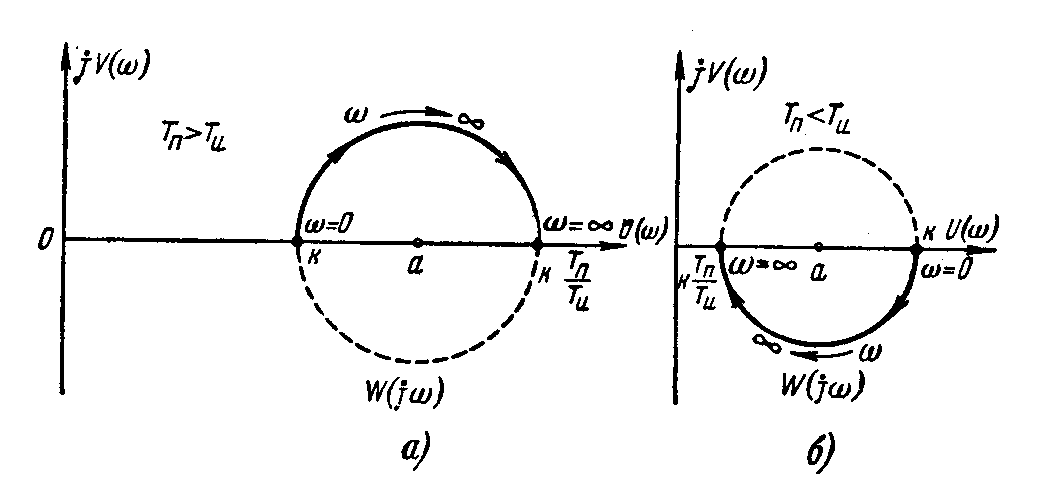
Рис. 3.28. АФХ интегро-дифференцирующего звена
АЧХ и ФЧХ звена приведены на рис. 3.29.
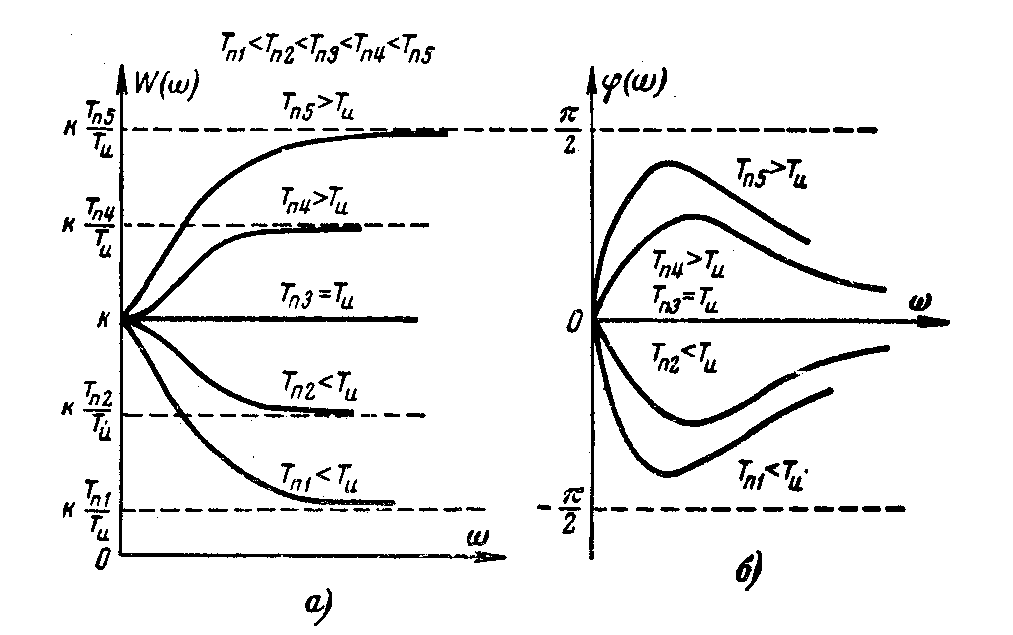
Рис. 3.29. Амплитудно-частотные и фазочастотные
характеристики интегро-дифференцирующего звена
На малых частотах
(![]() )
входных колебаний интегро-дифференцирующее
звено ведет как усилительное с
коэффициентом усиления
)
входных колебаний интегро-дифференцирующее
звено ведет как усилительное с
коэффициентом усиления
![]() .
При этом колебания проходят через звено
без искажений по фазе, т.к
.
При этом колебания проходят через звено
без искажений по фазе, т.к
![]() .
.
На больших частотах
входных колебаний (![]() )
звено также ведет себя как усилительное,
но с коэффициентом усиления, равным
)
звено также ведет себя как усилительное,
но с коэффициентом усиления, равным
![]() .
При этом ФЧХ также стремится к нулю.
.
При этом ФЧХ также стремится к нулю.
На средних частотах
выходные колебания или опережают
входные колебания (![]() ),
или отстают от них (
),
или отстают от них (![]() ).
).
При
![]() интегро-дифференцирующее звено по
своим свойствам приближается к
дифференцирующему звену. Если при этом
интегро-дифференцирующее звено по
своим свойствам приближается к
дифференцирующему звену. Если при этом
![]() ,
а
,
а
![]() ,
но так, что произведение
,
но так, что произведение
![]() – конечная постоянная величина, получаем
реальное дифференцирующее звено (см.
рис. 3.19).
– конечная постоянная величина, получаем
реальное дифференцирующее звено (см.
рис. 3.19).
При
![]() интегро-дифференцирующее звено по
своим свойствам приближается или к
интегрирующему, или к апериодическому.
интегро-дифференцирующее звено по
своим свойствам приближается или к
интегрирующему, или к апериодическому.
При
![]() ,
а
,
а
![]() ,
,
![]()
![]() ,
на при этом отношение
,
на при этом отношение
![]() является
конечной постоянной величиной, то звено
превращается в интегрирующее.
является
конечной постоянной величиной, то звено
превращается в интегрирующее.
Если при
![]() величины
величины
![]() конечны, получаем апериодическое звено.
конечны, получаем апериодическое звено.
При
![]() интегро-дифференцирующее звено
превращается в усилительное с
коэффициентом усиления
интегро-дифференцирующее звено
превращается в усилительное с
коэффициентом усиления
![]() .
При этом на всех частотах сигнал проходит
через звено без фазовых искажений.
Физически это можно объяснить тем, что
дифференцирующая составляющая дает
опережение выходной величины по
отношению к входной. Интегрирующая
же составляющая, наоборот создает
отставание выходной величины от
входной. При равенстве этих составляющих
они взаимно уравновешивают друг друга,
и результирующее воздействие их на
фазу выходного сигнала равно нулю.
.
При этом на всех частотах сигнал проходит
через звено без фазовых искажений.
Физически это можно объяснить тем, что
дифференцирующая составляющая дает
опережение выходной величины по
отношению к входной. Интегрирующая
же составляющая, наоборот создает
отставание выходной величины от
входной. При равенстве этих составляющих
они взаимно уравновешивают друг друга,
и результирующее воздействие их на
фазу выходного сигнала равно нулю.
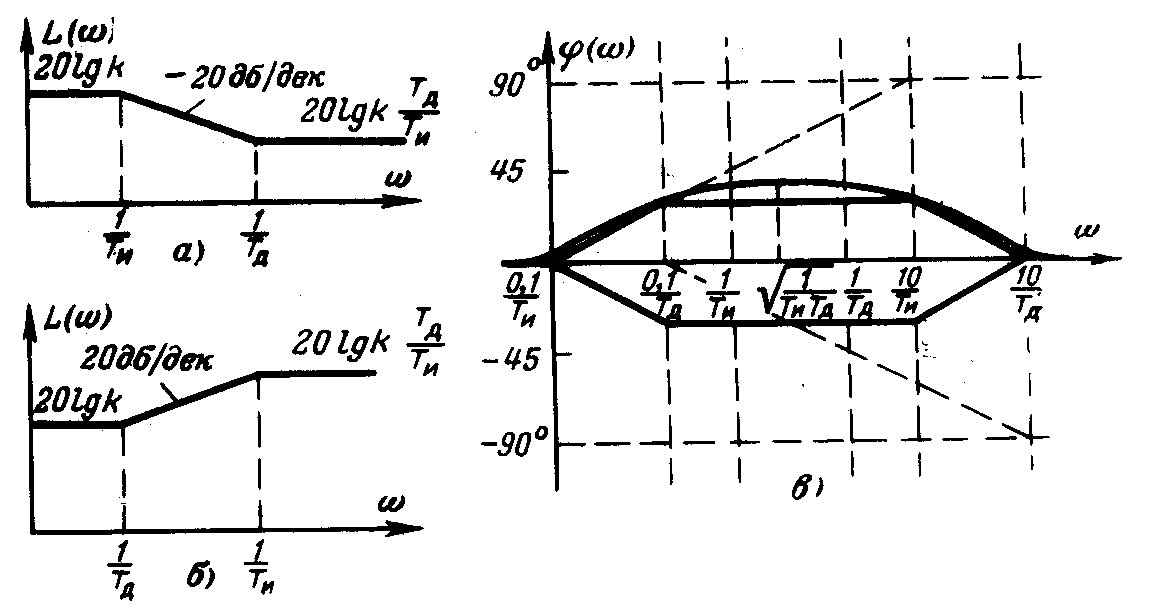
Рис. 3.30. Логарифмические частотные характеристики
интегро-дифференцирующего
звена при разных отношениях
![]()
Логарифмируя
выражение (3.36)
![]() ,
получим логарифмическую АЧХ звена:
,
получим логарифмическую АЧХ звена:
![]() . (3.39)
. (3.39)
Из этого выражения
следует, что вид аппроксимированной
ЛАЧХ звена зависит от соотношения
постоянных времени
![]() и
и
![]() .
.
При
![]() в интервале между сопрягающими частотами
в интервале между сопрягающими частотами
![]() и
и
![]() асимптота определяется отрезком прямой
с наклоном -20 дБ/дек (рис. 3.30, а).
асимптота определяется отрезком прямой
с наклоном -20 дБ/дек (рис. 3.30, а).
При
![]() сопрягающие частоты
сопрягающие частоты
![]() и
и
![]() ,
а асимптота в этом диапазоне частот
определяется отрезком прямой с наклоном
+20 дБ/дек (рис. 3.30, б).
В интервале низких частот
,
а асимптота в этом диапазоне частот
определяется отрезком прямой с наклоном
+20 дБ/дек (рис. 3.30, б).
В интервале низких частот
![]() ЛАЧХ аппроксимируется прямой
ЛАЧХ аппроксимируется прямой
![]() ,
а в интервале высоких частот
,
а в интервале высоких частот
![]() – прямой
– прямой
![]() .
На рис. 3.30, в
приведены аппроксимированные ЛАЧХ как
при
.
На рис. 3.30, в
приведены аппроксимированные ЛАЧХ как
при
![]() ,
так и при
,
так и при
![]() .
.
При последовательном соединении двух интегро-дифференцирующих звеньев получаем также интегро-дифференцирующее звено . Амплитудно-фазовая характеристика звена
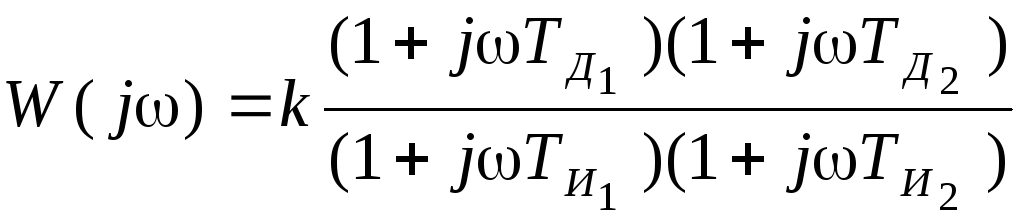 . (3.40)
. (3.40)
Логарифмическая амплитудно-частотная характеристика
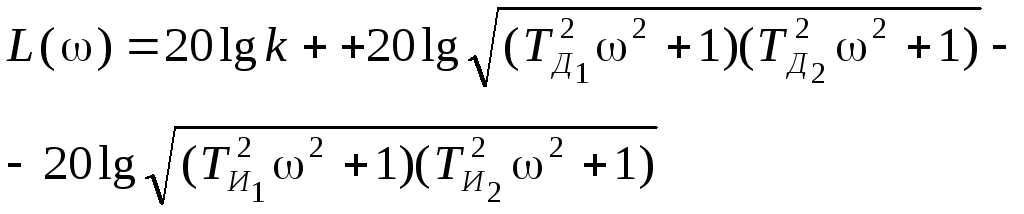 (3.41)
(3.41)
Фазо-частотная характеристика звена
![]()
Частотные
характеристики комбинированного
интегро-дифференцирующего звена
второго порядка, представленного
![]() -
цепью, изображенной на рис. 2.13, а,
приведены на рис. 3.31.
-
цепью, изображенной на рис. 2.13, а,
приведены на рис. 3.31.
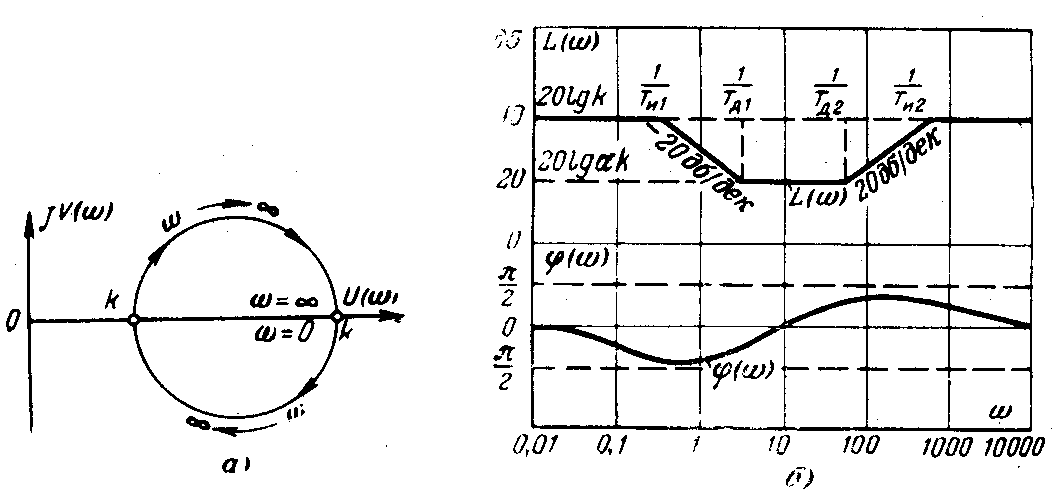
Рис. 3.31. АФХ и ЛЧХ комбинированного
интегро-дифференцирующего звена
Такое комбинированное звено (3.40) имеет принципиальное отличие от звена (3.34), которое заключается в следующем: на низких частотах это соединение ведет себя как интегрирующее, а в области высоких частот – как дифференцирующее устройство.
В связи с этим такое комбинированное устройство с АФХ вида (3.40) на практике широко применяются для построения и улучшения динамических свойств АСР.
