5. Инерционное звено второго порядка
В соответствии с передаточной функцией инерционного звена второго порядка
АФХ можно записать в виде:
Вещественная частотная характеристика
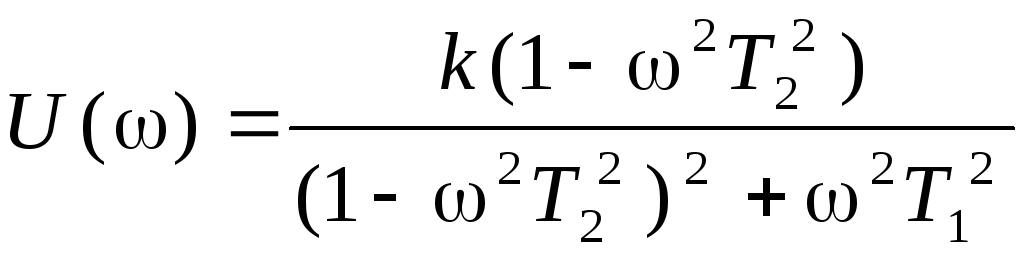
Мнимая частотная характеристика
Амплитудно-частотная характеристика
Фазо-частотная характеристика
На рис. 3.20 изображена амплитудно-фазовая характеристика (АФХ) звена.
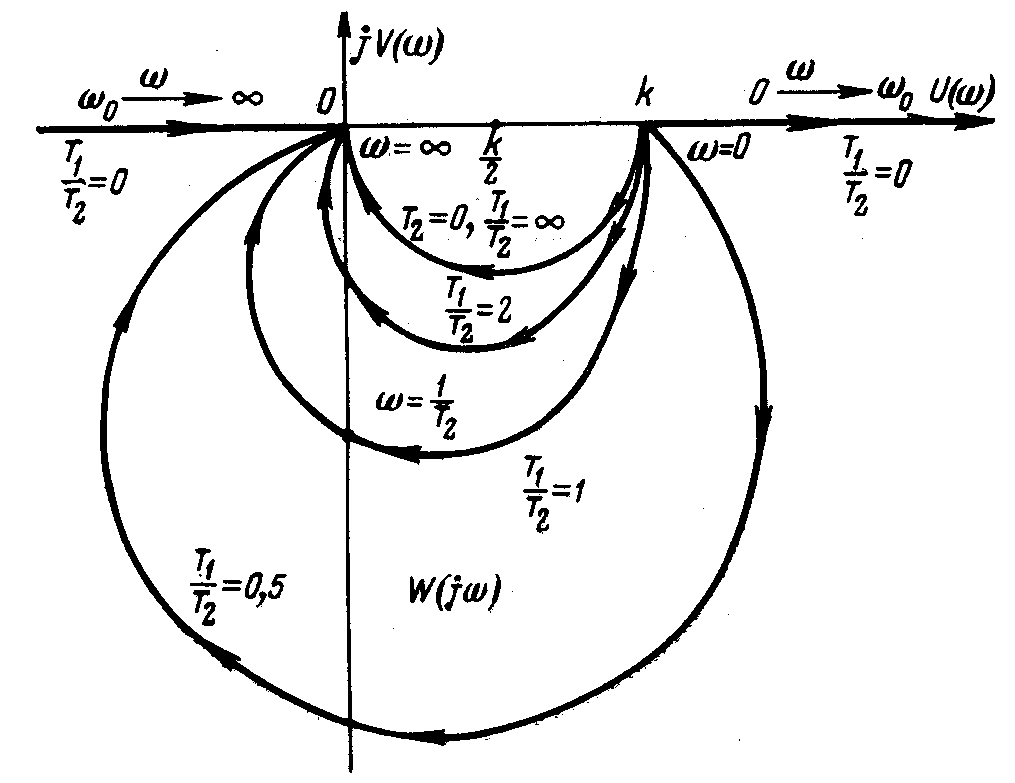
Рис. 3.20. АФХ инерционного звена второго порядка
при разном отношении
АФХ
начинается на действительной оси в
точке с абсциссой, равной
.
Вид АФХ определяется величиной отношения
постоянных времени
.
Чем больше это отношение, тем меньше
колебательность звена. При
колебательное звено превращается в
соединение из двух апериодических
звеньев первого порядка.
При
и
отношение
,
а инерционное звено второго порядка
превращается в инерционное звено
первого порядка с постоянной времени
.
Амплитудно-фазовая характеристика в
этом случае определяется выражением
,
и имеет вид
окружности с радиусом
,
центр которой расположен на вещественной
оси в точке (
).
При
инерционное звено второго порядка
превращается в колебательное звено
(соотношение 2.49).
При этом, чем
меньше
,
тем меньше отношение
и
тем меньше степень затухания колебаний
в звене (соотношение (2.51).
При
степень затухания
будет равна нулю и возникшие в звене
колебания будут незатухающими с
собственной частотой колебаний, равной
.
Амплитудно-фазовая характеристика при этом определяется выражением
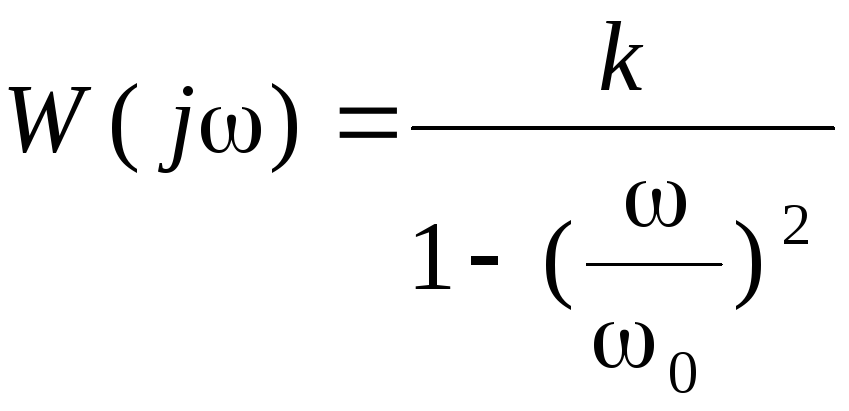. (3.31)
Графически эта
характеристика при изменении частоты
колебаний входной величины
имеет вид двух полупрямых
(рис. 3.20).
Первая полупрямая начинается при
на вещественной положительной полуоси
в точке
и при возрастании
уходит в бесконечность по вещественной
полуоси в положительном направлении.
Вторая полупрямая совпадает с
отрицательной вещественной полуосью.
Начало прямой в бесконечности при
,
а конец – в начале координат при
,
т.е. функция не определена и терпит
разрыв на частоте
.
Такой разрыв графически представляют
окружностью бесконечного радиуса, а
функцию для практического использования
доопределяют затуханием
Определяя первую производную АЧХ по частоте и приравнивая полученное выражение нулю, находим:
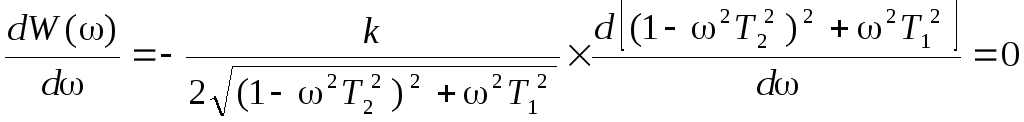
Отсюда вытекает, что
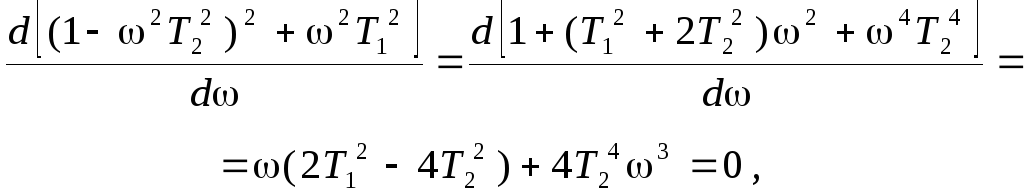
или
Из этого уравнения находим значение частот, при которых АЧХ имеет экстремумы:
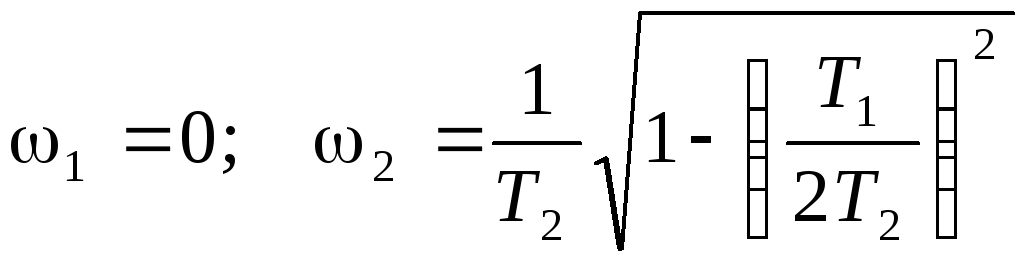
Из выражения для
АЧХ следует, что при
АЧХ равна коэффициенту усиления
инерционного звена второго порядка:
,
и не зависит от
величины постоянных времени
,
и их соотношения.
Второе вещественное
экстремальное значение
имеется только при
.
При этом чем больше
отношение постоянных времени приближается
к значению
,
тем ближе подходит вторая точка
экстремума к первой (это видно из рис.
3.21, а).
Рассмотрим второй
экстремум кривой
,
появляющийся при
.
Из рисунка видно, (и это можно аналитически
показать на АЧХ), что при возрастании
от
до
АЧХ также возрастает, начиная со значения
,
и при
достигает максимального значения:
,
при дальнейшем увеличении частоты АЧХ стремится к нулю.
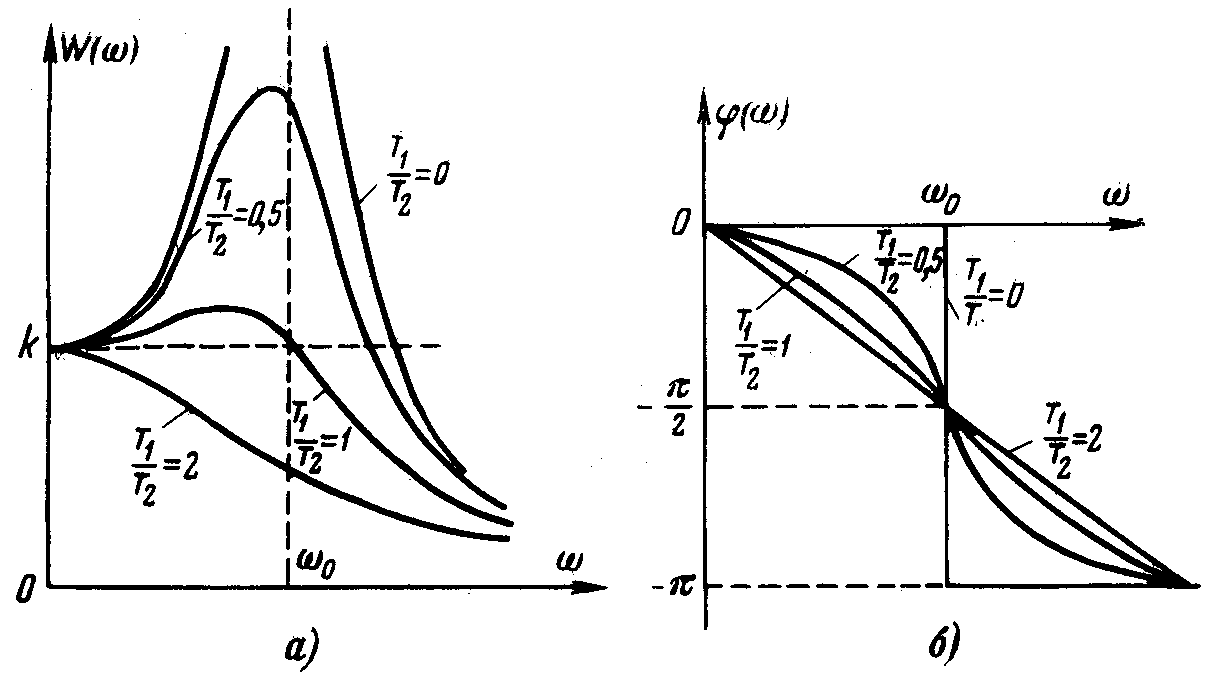
Рис. 3.21
Амплитудно-частотные
и фазочастотные
характеристики инерционного звена второго порядка
Если продолжить
дальнейшее уменьшение отношения
,
максимум АЧХ увеличивается и приближается
к собственной частоте колебаний звена
.
При
максимум
.
Амплитудно-частотная характеристика
при этом совпадает с амплитудно-фазовой
и определяется выражением (3.31).
Итак, если входная
величина является постоянной (
),
то
.
Если частота входной величины стремится
к бесконечности, то амплитудно-частотная
характеристика стремится к нулю, что
явствует из рисунка.
Из рисунка 3.21, б
видно, что всё семейство характеристик
для различных отношений
равно нулю при
,
равно
при частоте
и стремится к
при частоте
.
Так как
отрицательна, то выходные колебания
во всем диапазоне изменения
отстают от входных колебаний.
При
фаза выходных колебаний совпадает с
фазой входных колебаний в диапазоне
изменений
от
.
При
происходит изменение фазы скачком от
до
,
и в диапазоне изменения
от
фаза выходных колебаний отстает от
фазы входных колебаний на
.
-
Построение асимптотических логарифмических
частотных характеристик (ЛЧХ)
Амплитудно-фазовую характеристику (АФХ) можно записать
Вначале построения
асимптотической ЛАХ проводятся
вспомогательные вертикальные линии
через сопрягающие частоты
и
.
Для определенности построения принято,
что
.
ЛАХ строится по выражению
. (**)
Построение ЛЧХ изображено на рис. 3.22.
Левее первой
сопрягающей частоты (
),
это выражение заменяется приближенным
,
которому соответствует горизонтальная прямая (первая асимптота ЛАХ).
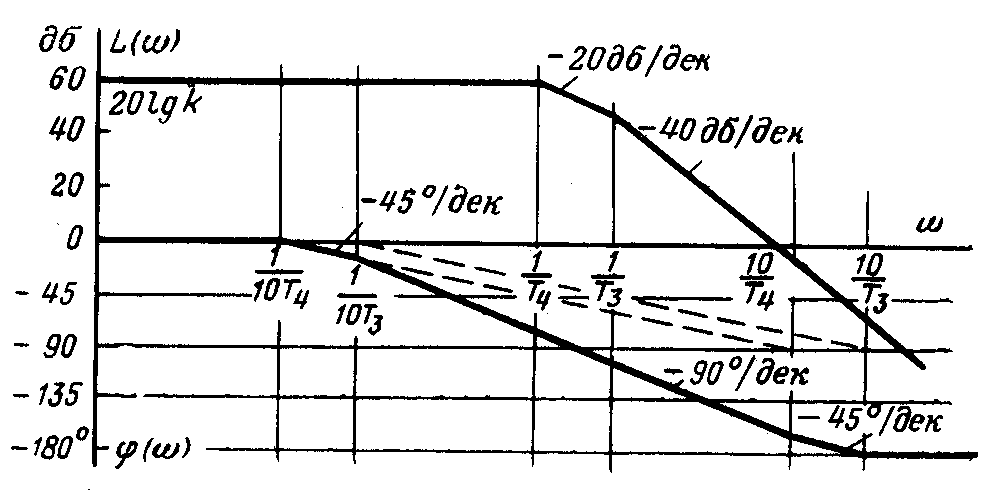
Рис. 3.22. Построение асимптотической ЛЧХ
Для
частот
выражение (**)
заменяется приближенным
,
которому
соответствует прямая с отрицательным
наклоном -20 дБ/дек (вторая асимптота).
Для частот
выражение (**) заменяется приближенным
,
которому соответствует прямая с отрицательным наклоном -40 дБ/дек. (третья асимптота). Действительная ЛАХ показана на рисунке пунктиром. Она отличается от асимптотической в точках излома на 3 дБ.
Фазо-частотная характеристика
.
На рис. 3.23 приведен листинг MathCAD-программы расчета и построения логарифмической частотной характеристики инерционного звена второго порядка для ЛАХ, отмеченной (**) с параметрами расчета:
.
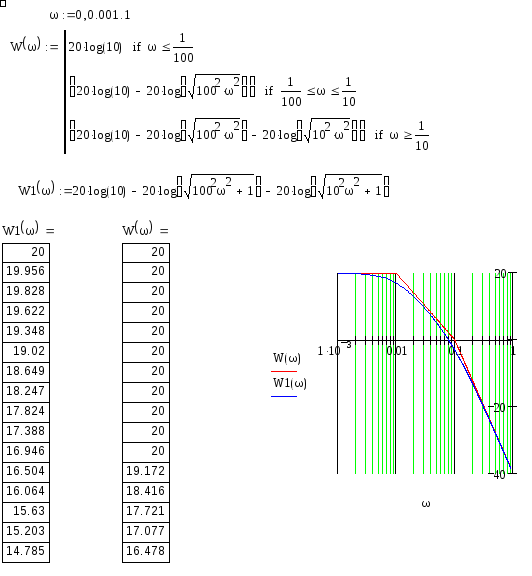
Рис. 3.23. Mathcad-программа расчета и построения ЛАЧХ
При
построении логарифмической фазочастотной
характеристики в соответствии с
выражением (3.17)
типа
,
в которых знаменатель
может быть нулевым или отрицательным.
Во избежание сингулярности (при
)
или ошибки (при
)
вычисления фазового сдвига
тригонометрических функций
необходима ручная коррекция главного
значения
,
возвращаемого функцией
,
с учетом знаков чисел
и
:
