
- •Основы теории автоматического управления Конспект лекций
- •Терминология
- •Введение
- •1. Классификация систем автоматического регулирования
- •1.1. Классификация по основному признаку
- •1.2. Общая классификация систем автоматического управления
- •2. Математические модели элементов и систем управления
- •2.1. Передаточные функции. Преобразования Лапласа
- •2.2. Типовых звенья и их передаточные функции
- •2.2.1. Усилительное (безынерционное) звено
- •2.2.2. Интегрирующие звенья
- •1. Идеальное интегрирующее звено
- •2. Интегрирующее звено с замедлением
- •3. Изодромное звено
- •2.2.3. Дифференцирующие звенья
- •1. Идеальное дифференцирующее звено
- •2. Дифференцирующее звено с замедлением
- •2.2.4. Инерционное звено первого порядка (апериодическое)
- •2.2.5. Интегро-дифференцирующее звено
- •2.2.6. Инерционное звено второго порядка
- •2.2.7. Запаздывающее звено
- •2.2.8. Представление реальных аср типовыми звеньями
- •3. Основные характеристики звеньев и систем
- •3.1. Статические свойства элементов и систем
- •3.2. Соединения статических элементов
- •3.3. Временные характеристики
- •3.4. Частотные характеристики
- •3.5. Частотные характеристики типовых звеньев
- •1. Частотная характеристика усилительного звена (безынерционного)
- •2. Частотные характеристики инерционного звена первого порядка
- •3. Частотные характеристики интегрирующего звена
- •4. Дифференцирующее звено
- •5. Инерционное звено второго порядка
- •6. Колебательное звено
- •7. Запаздывающее звено
- •8. Частотные характеристики интегро-дифференцирующих звеньев и их соединений
- •3.6. Соединение звеньев. Передаточные функции соединений
- •1. Последовательное соединение звеньев
- •2. Параллельное соединение звеньев
- •3. Встречно-параллельное соединение звеньев или соединение с обратной связью
- •4. Эквивалентные преобразования структурных схем
- •3. Пропорцилнально-интегральные регуляторы
- •4. Пропорционально-интегрально-дифференциольные регуляторы
- •3.8. Последовательные и параллельные корректирующие устройства
- •3.9 Передаточные функции систем автоматического регулирования
- •4. Импульсные системы
- •4.1. Математическое описание дискретных объектов управления в электромеханических системах
- •4.2. Общие сведения об импульсных системах
- •4.3. Цифровые регуляторы в электромеханических системах
- •4.3.1. Методика синтеза регуляторов в мехатронной системе
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Постановка задачи исследования устойчивости
- •5.2. Оценка устойчивости разомкнутой и замкнутой системы с помощью алгебраического критерия Рауса-Гурвица
- •5.3. Частотные критерии устойчивости
- •1. Критерий Михайлова
- •2. Критерий устойчивости Найквиста
- •Приложения
- •Список литературы
- •Оглавление
3.5. Частотные характеристики типовых звеньев
1. Частотная характеристика усилительного звена (безынерционного)
Исходя из выражения
(2.9), переходя от
![]() ,
можно записать:
,
можно записать:
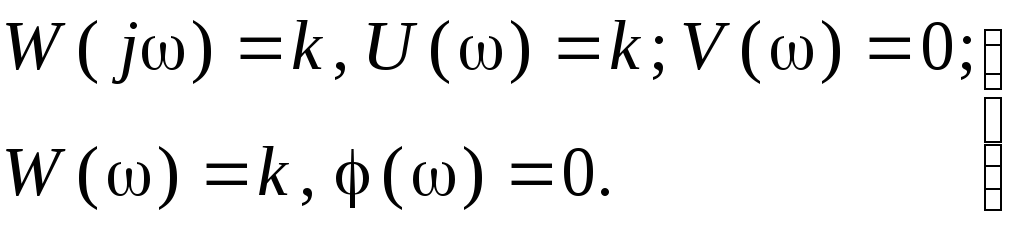 (3.18)
(3.18)
Таким образом, АФХ усилительного звена представляет собой вектор, совпадающий с положительным направлением оси абсцисс, модуль которого не зависит от частоты и равен коэффициенту передачи звена.
Воздействия любой частоты, поступающие на вход этого звена, усиливаются в одинаковой степени без фазового сдвига.
Логарифмическая АЧХ звена определяется выражением
![]() ,
(3.19)
,
(3.19)
и представляет
собой прямую, параллельную оси абсцисс
и проходящую от нее на расстоянии
![]() .
Логарифмическая ФЧХ при всех частотах
совпадает с осью абсцисс, так как фазовый
сдвиг при всех частотах равен нулю.
.
Логарифмическая ФЧХ при всех частотах
совпадает с осью абсцисс, так как фазовый
сдвиг при всех частотах равен нулю.
2. Частотные характеристики инерционного звена первого порядка
Из передаточной
функции звена
![]() находим его АФХ:
находим его АФХ:
![]() (3.20)
(3.20)
Вещественная и мнимая частотные характеристики
![]() . (3.21)
. (3.21)
Согласно уравнениям (3.16) и (3.17) АЧХ и ФЧХ имеют вид:
![]() (3.22)
(3.22)
Задаваясь различными
значениями
![]() ,
можно по выражениям (3.21) построить АФХ
звена. Однако в данном случае можно из
этих же двух уравнений параметрически
получить на плоскости
,
можно по выражениям (3.21) построить АФХ
звена. Однако в данном случае можно из
этих же двух уравнений параметрически
получить на плоскости
![]() уравнение кривой
уравнение кривой
![]() в явном виде как функцию.
в явном виде как функцию.
Складывая выражения (3.21), получим:
![]() .
.
Возводя в квадрат левую и правую части равенства, найдем:

откуда
![]()
Прибавляя к обеим
частям этого равенства слагаемое
![]() ,
получаем:
,
получаем:
![]() (3.23)
(3.23)
Из полученного
уравнения следует, что АФХ имеет вид
окружности (рис. 3.13, а)
с радиусом
![]() ,
центр которой расположен на положительной
вещественной полуоси в точке с
координатами (
,
центр которой расположен на положительной
вещественной полуоси в точке с
координатами (![]() ).
Окружность касается мнимой оси в начале
координат.
).
Окружность касается мнимой оси в начале
координат.
Изменениям
![]() от
от
![]() соответствует
полуокружность, расположенная в
четвертом квадранте, а изменениям
соответствует
полуокружность, расположенная в
четвертом квадранте, а изменениям
![]() от
от
![]() – полуокружность в первом квадранте.
– полуокружность в первом квадранте.
Из графиков
частотных характеристик, представленных
на рисунке, видно, усиление звена по
амплитуде при увеличении частоты
уменьшается. Это уменьшение тем резче,
чем больше постоянная времени
![]() .
.
С ростом частоты
увеличивается также фазовый сдвиг
выходных колебаний п отношению к
входным. Фазо-частотная характеристика
звена отрицательна, следовательно,
выходные колебания звена по фазе отстают
от входных. При одной и той же частоте
фазовый сдвиг тем больше, чем больше
постоянная времени звена. При частотах,
амплитуда которых больше
![]() ,
т.е. в рабочей полосе частот (
,
т.е. в рабочей полосе частот (![]() )
апериодическое звено ведет себя как
усилительное. При увеличении входных
частот выходная величина звена по
модулю стремится к нулю, а фаза
)
апериодическое звено ведет себя как
усилительное. При увеличении входных
частот выходная величина звена по
модулю стремится к нулю, а фаза
![]() .
.
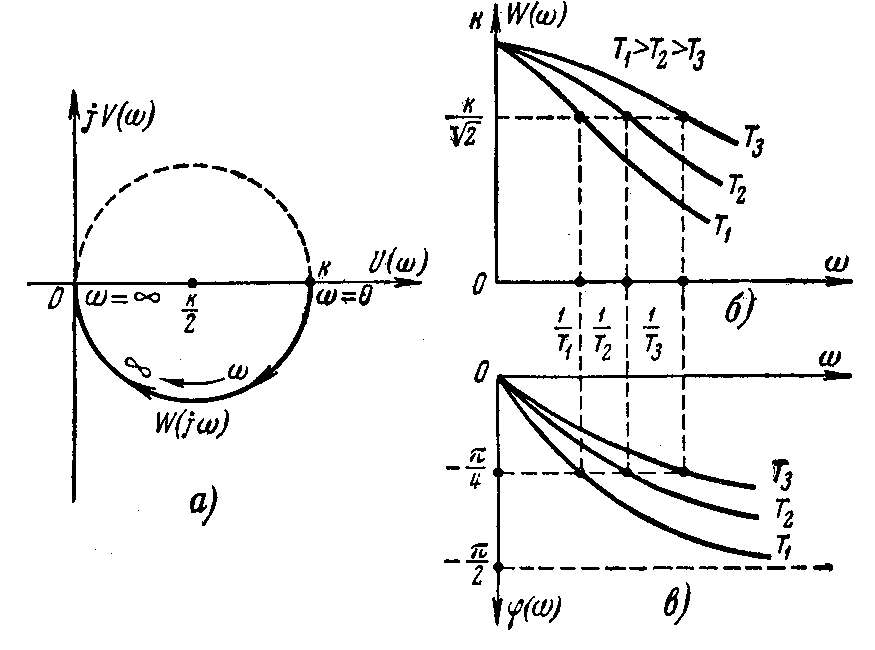
Рис. 3.13. Частотные характеристики апериодического звена
Характерным для
звена является
![]() ,
что ясно видно из выражений (3.22).
,
что ясно видно из выражений (3.22).
Логарифмируя выражение для АЧХ (3.22), найдем действительную характеристику
![]() . (*)
. (*)
Однако для целей практического использования часто бывает достаточно построить асимптотическую логарифмическую АЧХ – ЛАЧХ.
Наиболее просто, практически без вычислительной работы строится асимптотическая ЛАЧХ по выражению (*). Построение показано на рис. 3.14.
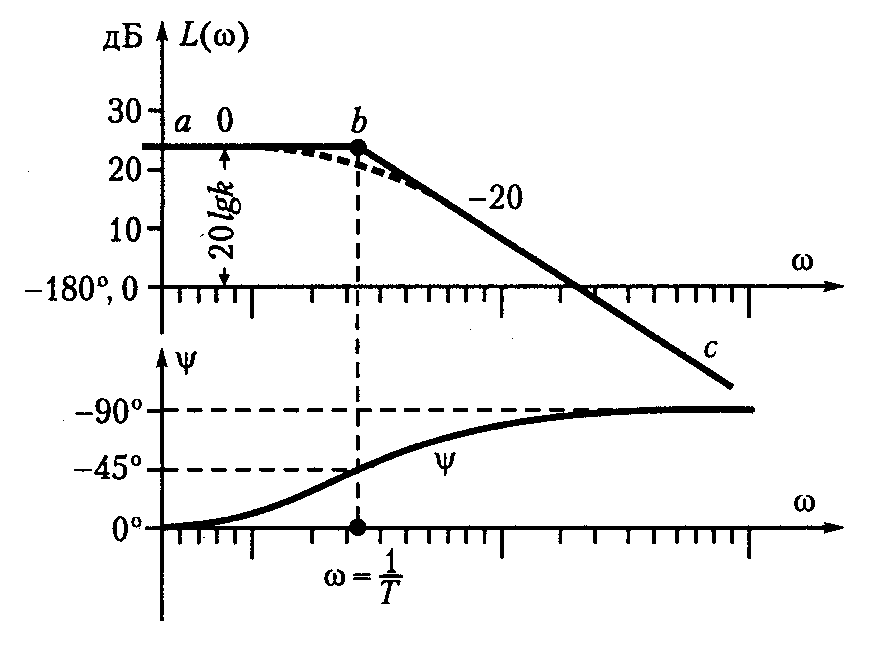
Рис. 3.14. Построение асимптотической ЛЧХ
На стандартной
сетку проводится вертикальная прямая
через точку с частотой, называемой
сопрягающей частотой
![]() .
Для частот меньших, чем сопрягающая,
т.е. при
.
Для частот меньших, чем сопрягающая,
т.е. при
![]() можно пренебречь первым слагаемым под
корнем в выражении (*). Тогда левее
сопрягающей частоты (рис. 3.14) можно
заменить (*) приближенным выражением
можно пренебречь первым слагаемым под
корнем в выражении (*). Тогда левее
сопрягающей частоты (рис. 3.14) можно
заменить (*) приближенным выражением
![]() ,
которому соответствует прямая линия,
параллельная оси частот. Прямая
,
которому соответствует прямая линия,
параллельная оси частот. Прямая
![]() является первой асимптотой.
является первой асимптотой.
Для частот больших,
чем сопрягающая (![]() )
в выражении (*) можно пренебречь под
корнем единицей по сравнению с
)
в выражении (*) можно пренебречь под
корнем единицей по сравнению с
![]() .
Тогда вместо (*) будем иметь приближенной
значение
.
Тогда вместо (*) будем иметь приближенной
значение
![]() ,
,
которому соответствует прямая с отрицательным наклоном -20 дБ/дек (прямая bc), являющаяся второй асимптотой.
Ломаная линия abc
называется асимптотической ЛАХ.
Действительная ЛАХ (показана на рис.
3.11 пунктиром) будет несколько отличаться
от асимптотической, причем наибольшее
отклонение будет наблюдаться в точке
![]() .
Оно равно приблизительно 3 дБ, так как
.
Оно равно приблизительно 3 дБ, так как
![]() дБ,
дБ,
что в линейном
масштабе соответствует отклонению в
![]() раз. На всем остальном протяжении влево
и вправо от сопрягающей частоты
действительная ЛАХ будет отличаться
от асимптотической менее чем на 3 дБ.
Поэтому во многих практических расчетах
достаточно ограничится построением
асимптотической ЛАХ. Что касается
построения логарифмической фазовой
характеристики, изображенной на
рис.3.14. Характерными ее особенностями
являются сдвиг по фазе
раз. На всем остальном протяжении влево
и вправо от сопрягающей частоты
действительная ЛАХ будет отличаться
от асимптотической менее чем на 3 дБ.
Поэтому во многих практических расчетах
достаточно ограничится построением
асимптотической ЛАХ. Что касается
построения логарифмической фазовой
характеристики, изображенной на
рис.3.14. Характерными ее особенностями
являются сдвиг по фазе
![]() на сопрягающей частоте (т.к.
на сопрягающей частоте (т.к.
![]() )
и симметрия ЛФХ относительно сопрягающей
частоты.
)
и симметрия ЛФХ относительно сопрягающей
частоты.
