
- •Основы теории автоматического управления Конспект лекций
- •Терминология
- •Введение
- •1. Классификация систем автоматического регулирования
- •1.1. Классификация по основному признаку
- •1.2. Общая классификация систем автоматического управления
- •2. Математические модели элементов и систем управления
- •2.1. Передаточные функции. Преобразования Лапласа
- •2.2. Типовых звенья и их передаточные функции
- •2.2.1. Усилительное (безынерционное) звено
- •2.2.2. Интегрирующие звенья
- •1. Идеальное интегрирующее звено
- •2. Интегрирующее звено с замедлением
- •3. Изодромное звено
- •2.2.3. Дифференцирующие звенья
- •1. Идеальное дифференцирующее звено
- •2. Дифференцирующее звено с замедлением
- •2.2.4. Инерционное звено первого порядка (апериодическое)
- •2.2.5. Интегро-дифференцирующее звено
- •2.2.6. Инерционное звено второго порядка
- •2.2.7. Запаздывающее звено
- •2.2.8. Представление реальных аср типовыми звеньями
- •3. Основные характеристики звеньев и систем
- •3.1. Статические свойства элементов и систем
- •3.2. Соединения статических элементов
- •3.3. Временные характеристики
- •3.4. Частотные характеристики
- •3.5. Частотные характеристики типовых звеньев
- •1. Частотная характеристика усилительного звена (безынерционного)
- •2. Частотные характеристики инерционного звена первого порядка
- •3. Частотные характеристики интегрирующего звена
- •4. Дифференцирующее звено
- •5. Инерционное звено второго порядка
- •6. Колебательное звено
- •7. Запаздывающее звено
- •8. Частотные характеристики интегро-дифференцирующих звеньев и их соединений
- •3.6. Соединение звеньев. Передаточные функции соединений
- •1. Последовательное соединение звеньев
- •2. Параллельное соединение звеньев
- •3. Встречно-параллельное соединение звеньев или соединение с обратной связью
- •4. Эквивалентные преобразования структурных схем
- •3. Пропорцилнально-интегральные регуляторы
- •4. Пропорционально-интегрально-дифференциольные регуляторы
- •3.8. Последовательные и параллельные корректирующие устройства
- •3.9 Передаточные функции систем автоматического регулирования
- •4. Импульсные системы
- •4.1. Математическое описание дискретных объектов управления в электромеханических системах
- •4.2. Общие сведения об импульсных системах
- •4.3. Цифровые регуляторы в электромеханических системах
- •4.3.1. Методика синтеза регуляторов в мехатронной системе
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Постановка задачи исследования устойчивости
- •5.2. Оценка устойчивости разомкнутой и замкнутой системы с помощью алгебраического критерия Рауса-Гурвица
- •5.3. Частотные критерии устойчивости
- •1. Критерий Михайлова
- •2. Критерий устойчивости Найквиста
- •Приложения
- •Список литературы
- •Оглавление
3. Основные характеристики звеньев и систем
3.1. Статические свойства элементов и систем
Статическим
называется элемент, у которого при
постоянном входном воздействии
![]() с течением времени, называемым временем
установления
с течением времени, называемым временем
установления
![]() ,
устанавливается постоянная выходная
переменная
,
устанавливается постоянная выходная
переменная
![]() .
Отношение
.
Отношение
![]() в установившемся режиме называется
коэффициентом усиления
в установившемся режиме называется
коэффициентом усиления
![]() .
.
Выходная величина
астатического элемента не имеет
установившегося значения, а неограниченно
возрастает с постоянной скоростью
(например, угол поворота электродвигателя
при постоянном входном напряжении),
ускорением (например, перемещение
материальной точки под действием
постоянной силы) или производной высшего
порядка. У такого элемента, например,
при постоянной установившейся скорости
изменения выходной переменной
![]() коэффициент усиления определяется как
отношение
коэффициент усиления определяется как
отношение
![]() .
.
Свойства статизма
или астатизма не абсолютны, а зависят
от выбора выходной переменной. Так,
если при описании электродвигателя в
качестве выходного сигнала задать не
угол поворота
![]() ,
а угловую скорость
,
а угловую скорость
![]() ,
то получим статический элемент. Признак
астатизма – наличие хотя бы одного
интегратора между входом и выходом
элемента или системы.
,
то получим статический элемент. Признак
астатизма – наличие хотя бы одного
интегратора между входом и выходом
элемента или системы.
Статической
характеристикой (СХ)
![]() (рис. 3.1, а) статического элемента
называется зависимость установившегося
значения выходной переменной от значения
постоянного входного воздействия.
Статическая характеристика, в общем
случае нелинейная, может быть гладкой
или разрывной (рис. 3.1, б), однозначной
или неоднозначной (например, гистерезисной
на рис. 3.1, в). Разрывные характеристики
присущи релейным элементам и
аналого-цифровым преобразователям.
Характеристиками гистерезисного типа
обладают, например, магнитные элементы
и механические соединения с люфтом.
(рис. 3.1, а) статического элемента
называется зависимость установившегося
значения выходной переменной от значения
постоянного входного воздействия.
Статическая характеристика, в общем
случае нелинейная, может быть гладкой
или разрывной (рис. 3.1, б), однозначной
или неоднозначной (например, гистерезисной
на рис. 3.1, в). Разрывные характеристики
присущи релейным элементам и
аналого-цифровым преобразователям.
Характеристиками гистерезисного типа
обладают, например, магнитные элементы
и механические соединения с люфтом.
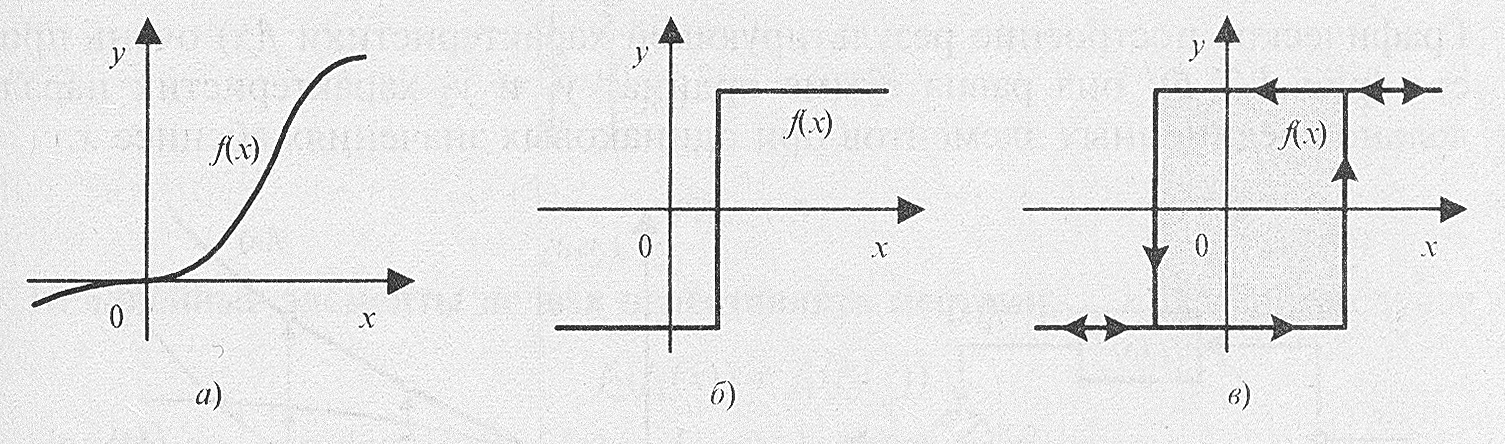
Рис. 3.1. Статические характеристики
Линейный статический
элемент имеет гладкую линейную
статическую характеристику
![]() ,
где
,
где
![]() – смещение в нуле, а коэффициент
– смещение в нуле, а коэффициент
![]() задает коэффициент усиления элемента
относительно приращений входного
задает коэффициент усиления элемента
относительно приращений входного
![]() и выходного
и выходного
![]() сигналов.
сигналов.
Астатический элемент не имеет статической характеристики по причине отсутствия установившегося режима при постоянном входном воздействии. Однако может существовать статическая характеристика
![]()
для
![]() -ой
производной выходного сигнала
-ой
производной выходного сигнала
![]() .
Минимальный порядок производной
.
Минимальный порядок производной
![]() ,
имеющей статическую характеристику,
называется порядком астатизма.
Он равен числу интеграторов между
входом и выходом, не охваченных контуром
обратной связи. Статические элементы
имеют астатизм нулевого порядка.
,
имеющей статическую характеристику,
называется порядком астатизма.
Он равен числу интеграторов между
входом и выходом, не охваченных контуром
обратной связи. Статические элементы
имеют астатизм нулевого порядка.
3.2. Соединения статических элементов
Статическая характеристика системы, образованной соединением двух элементов, может быть найдена двумя способами:
-
аналитическим, если заданы формулы статических характеристик исходных элементов;
-
графическим, если характеристики элементов заданы графиками.
Рассмотрим основные типы соединений статических элементов и методы аналитического и графического расчета их статических характеристик.
-
Параллельное соединение (рис. 3.2, а):
![]() .
.
Графическое
построение результирующей характеристики
![]() очень
просто: она равна сумме ординат
очень
просто: она равна сумме ординат
![]() и
и
![]() характеристик, параллельно соединенных
элементов при одинаковых значениях
абсцисс
характеристик, параллельно соединенных
элементов при одинаковых значениях
абсцисс
![]() (рис. 3.2, б).
(рис. 3.2, б).
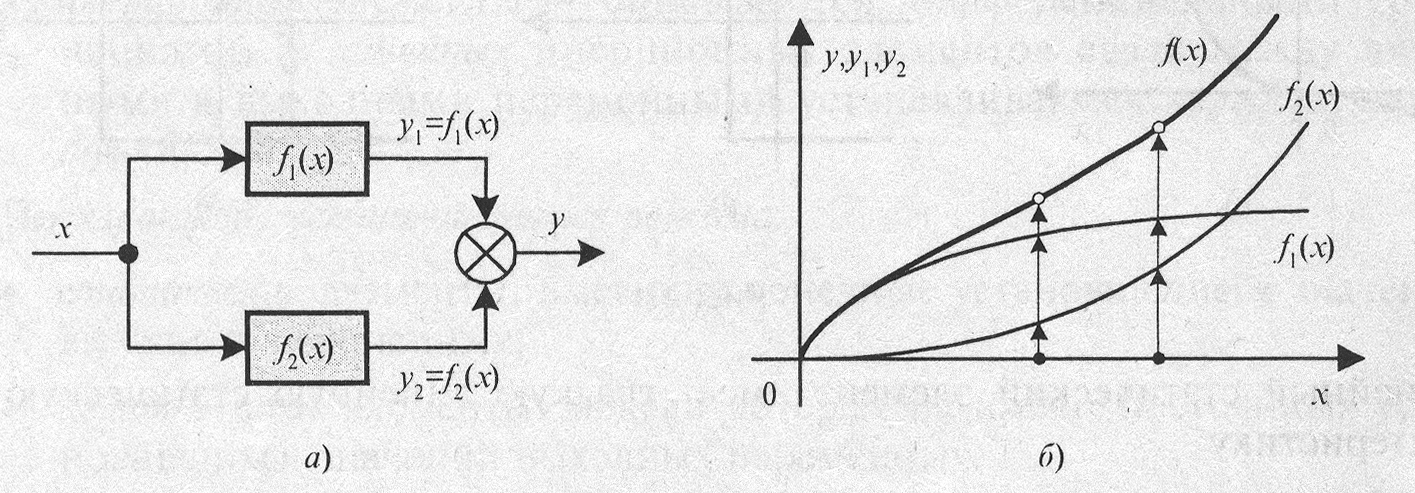
Рис. 3.2. Графическое
построение
результирующей характеристики
![]()
-
Последовательное соединение (рис. 3.3, а):
![]() .
.
Графическое
построение результирующей характеристики
![]() выполняется следующим образом (рис.
3.3, б):
выполняется следующим образом (рис.
3.3, б):
-
на оси абсцисс характеристики первого элемента выбираем значение
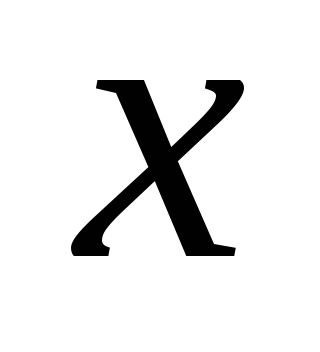 и по графику
и по графику
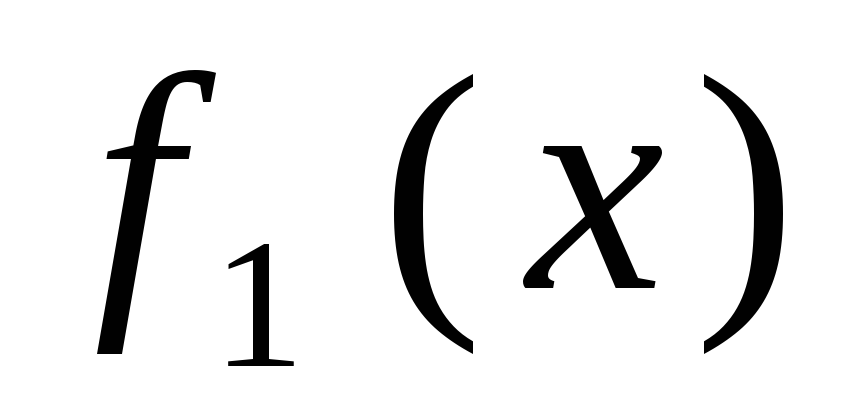 определяем выходной сигнал
определяем выходной сигнал
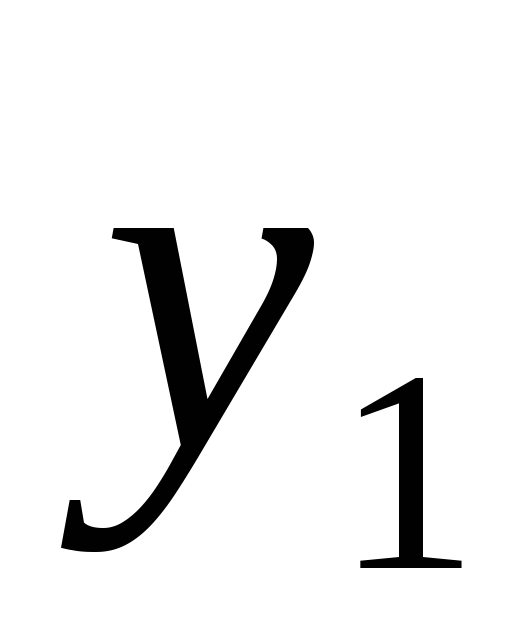 ;
; -
рассматривая
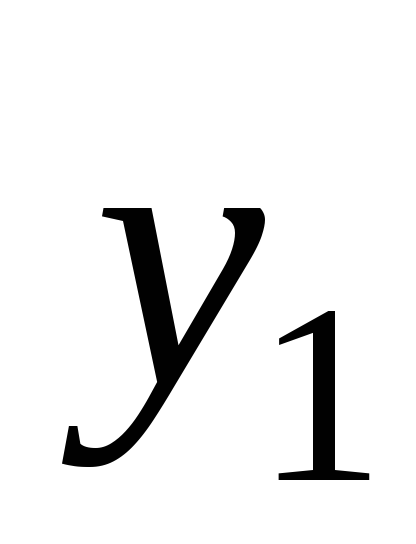 как входной сигнал второго элемента,
по графику
как входной сигнал второго элемента,
по графику
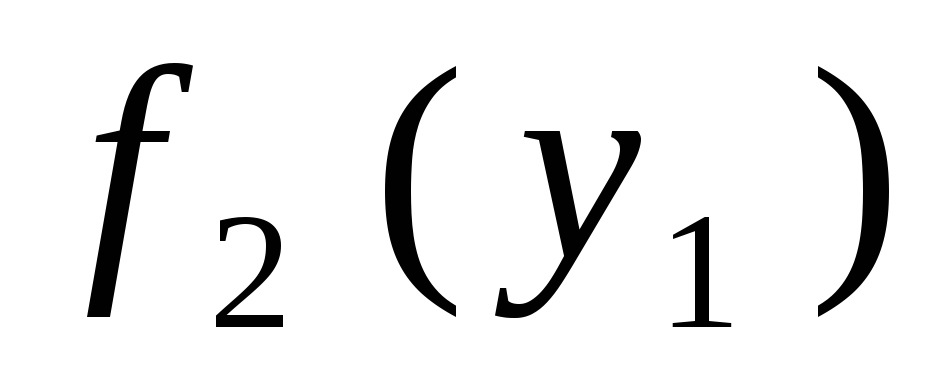 находим значение
находим значение
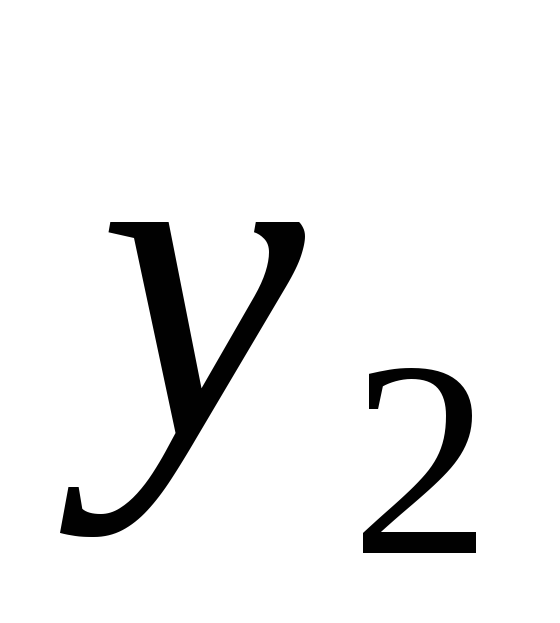 ,
равное выходному сигналу
,
равное выходному сигналу
 последовательного соединения. При
этом ось
последовательного соединения. При
этом ось
 совпадает с осью
совпадает с осью
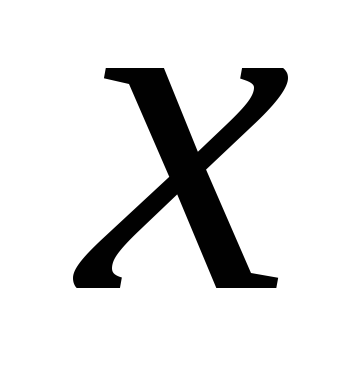 ;
; -
для каждой пары чисел
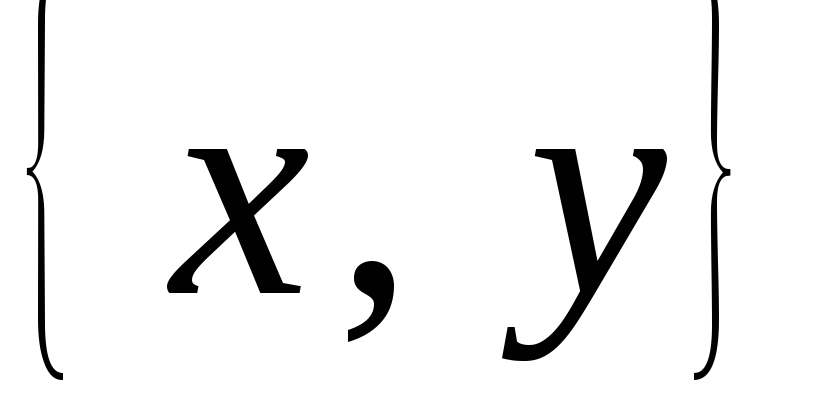 на отдельном графике строим точку
искомой характеристики
на отдельном графике строим точку
искомой характеристики
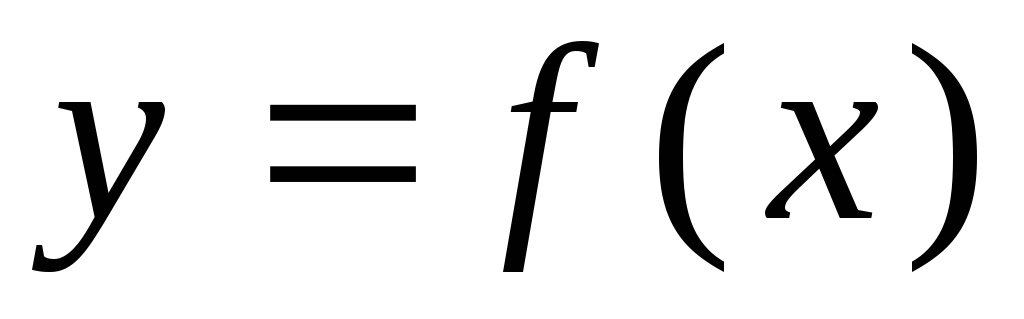 .
.
Нелинейные элементы нельзя переставлять местами, т.к. в общем случае
![]() .
.
Например, для
функций
![]() и
и
![]() имеем
имеем
![]() .
.
-
Соединение с обратной связью (рис. 3.4, а). На рисунке и формулах в обозначениях «
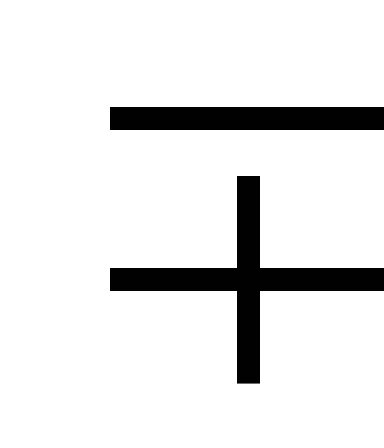 »
верхний знак означает отрицательную
обратную связь (ООС), а нижний положительную
(ПОС).
»
верхний знак означает отрицательную
обратную связь (ООС), а нижний положительную
(ПОС).
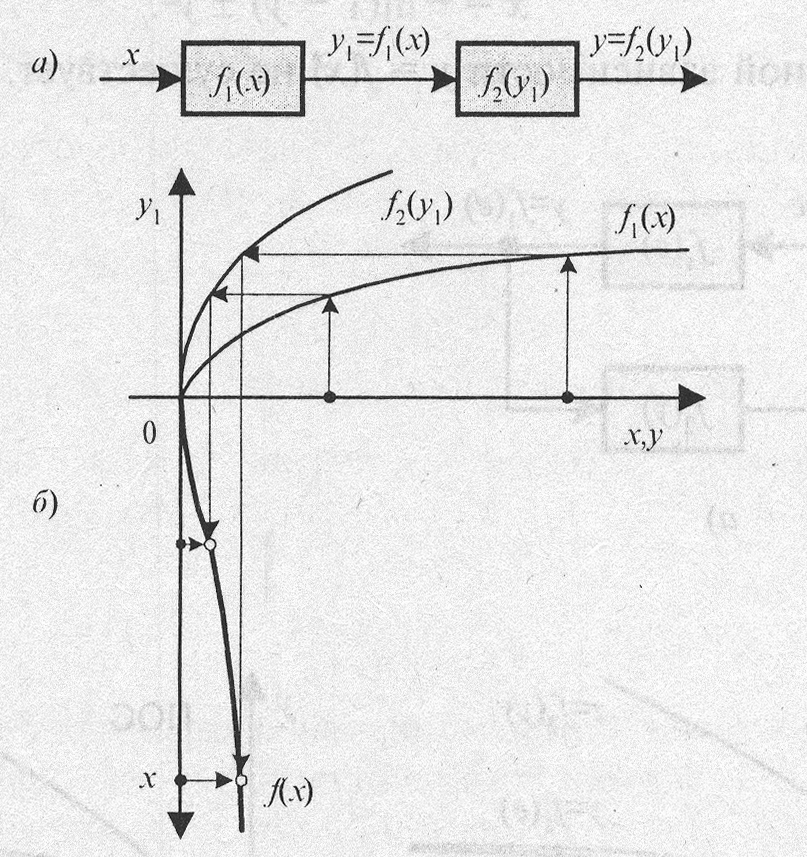
Рис. 3.3. Графическое
построение
результирующей характеристики
![]()
Запишем уравнение трех блоков системы:
![]() .
.
Исключая переменные
![]() и
и
![]() ,
получим уравнение связи входа и выхода:
,
получим уравнение связи входа и выхода:
![]() .
.
Оно имеет решение
в виде функции, обратной к статической
характеристике
![]() :
:
![]() .
.
Аналитическое обращение нелинейной функции не всегда возможно.
Так, для функции
![]() и
и
![]() получим
получим
![]() ,
откуда следует обратная зависимость
,
откуда следует обратная зависимость
![]() .
.
Откуда видно, что
явной зависимости
![]() не существует.
не существует.
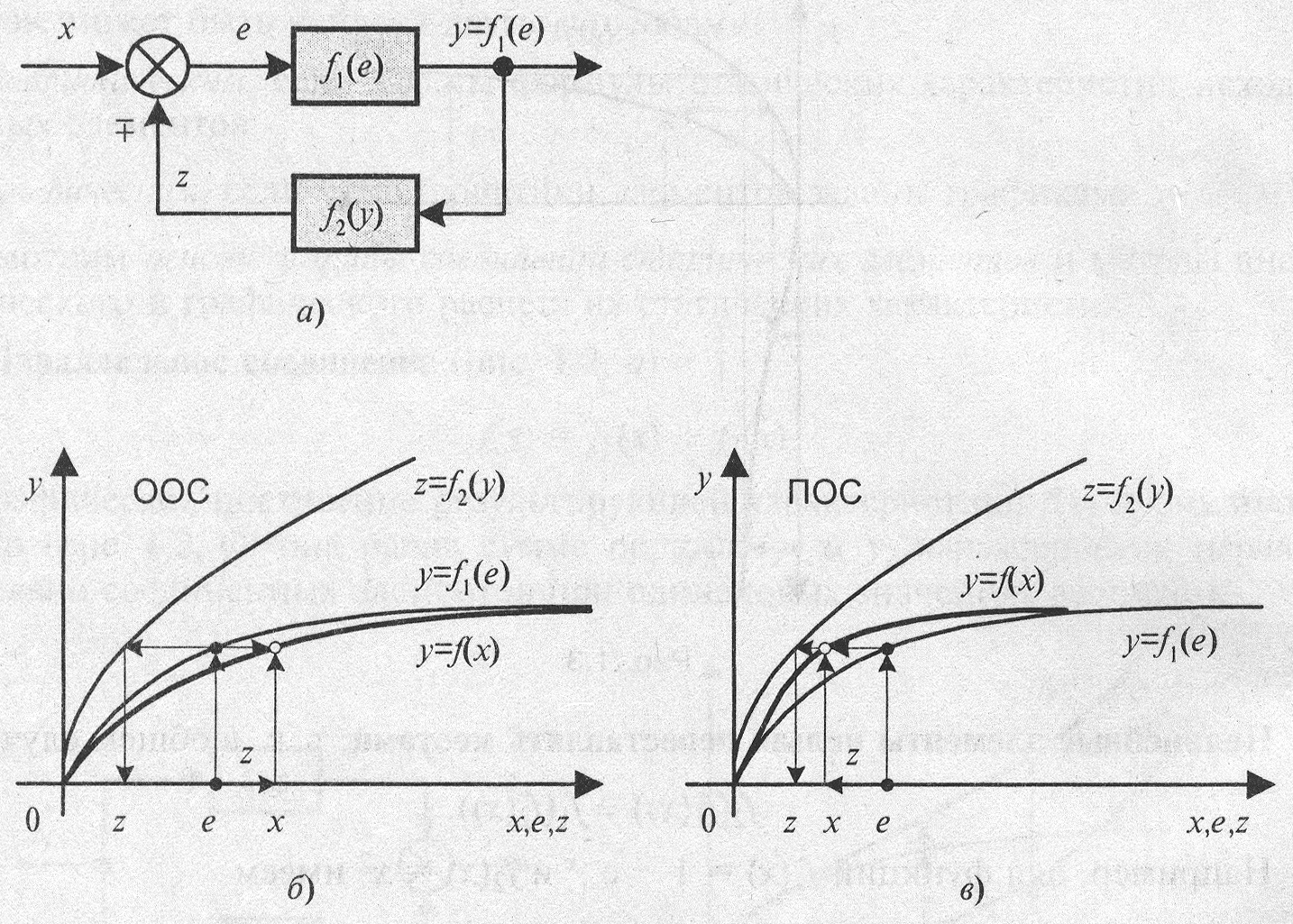
Рис. 3.4. Соединение с обратной связью
Последовательность графического построения статической характеристики обратного соединения
![]()
дает функцию
![]() для каждого значения
для каждого значения
![]() ,
и показана стрелками для случаев
отрицательной (рис. 3.4, б) и положительной
(рис. 3.4, в) обратных связей.
,
и показана стрелками для случаев
отрицательной (рис. 3.4, б) и положительной
(рис. 3.4, в) обратных связей.
