Предел на бесконечности по Коши

• Пусть числовая функция задана на множестве , в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка . В этом случае число называется пределом функции на бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, превышающих по абсолютному значению, справедливо неравенство .

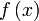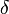• Пусть числовая функция задана на множестве , в котором для любого числа найдётся элемент, лежащий правее него. В этом случае число называется пределом функции на плюс бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, лежащих правее 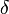, справедливо неравенство .

• Пусть числовая функция задана на множестве , в котором для любого числа найдётся элемент, лежащий левее него. В этом случае число называется пределом функции на минус бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, лежащих левее , справедливо неравенство .

Окрестностное определение по Коши

Пусть функция определена на множестве , имеющем элементы вне любой окрестности нуля. В этом случае точка называется пределом функции на бесконечности, если для любой её малой окрестности найдётся достаточно большая окрестность нуля, что значения функции в точках, лежащих вне этой окрестности нуля, попадают в эту окрестность точки .

Обозначения

Если в точке у функции существует предел, равный , то говорят, что функция стремится к при стремлении к , и пишут одним из следующих способов:

• , или

• .

Если у функции существует предел на бесконечности, равный , то говорят, что функция стремится к при стремлении к бесконечности, и пишут одним из следующих способов:

• , или

• .

Если у функции существует предел на плюс бесконечности, равный , то говорят, что функция стремится к при стремлении к плюс бесконечности, и пишут одним из следующих способов:

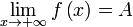• , или

• .

Если у функции существует предел на минус бесконечности, равный , то говорят, что функция стремится к при стремлении к минус бесконечности, и пишут одним из следующих способов:

• , или

• .

Свойства пределов числовых функций

Пусть даны функции и .

• Одна и та же функция в одной и той же точке может иметь только один предел.

Доказательство  

    Доказательство методом от противного. Пусть существует и и . Предположим A₁ < A₂. Возьмём , такое что A₁ + ε < A₂ − ε, т.е. .

, т.е. A₁ − ε < f(x) < A₁ + ε.

, т.е. A₂ − ε < f(x) < A₂ + ε.

Тогда получаем    Противоречие. Значит предел единственный.    

• Сходящаяся функция локально сохраняет знак. Более обще,

где  — проколотая окрестность точки a.

• В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:

• Сходящаяся функция локально ограничена в окрестности предельной точки:

• Отделимость от нуля функций, имеющих предел, отличный от нуля.

• Операция взятия предела сохраняет нестрогие неравенства.

• Правило двух милиционеров

• Предел суммы равен сумме пределов:

• Предел разности равен разности пределов:

• Предел произведения равен произведению пределов:

• Предел частного равен частному пределов.