Критерий ограниченности числовой последовательности

Числовая последовательность является ограниченной тогда и только тогда, когда существует такое число, что модули всех членов последовательности не превышают его.

(x_n) ограниченная

Свойства ограниченных последовательностей

• Ограниченная сверху числовая последовательность имеет бесконечно много верхних граней.

• Ограниченная снизу числовая последовательность имеет бесконечно много нижних граней.

• Ограниченная последовательность имеет по крайней мере одну предельную точку.

• У ограниченной последовательности существуют верхний и нижний пределы.

• Для любого наперёд взятого положительного числа ε все элементы ограниченной числовой последовательности , начиная с некоторого номера, зависящего от ε, лежат внутри интервала .

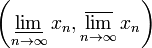• Если за пределами интервала лежит лишь конечное число элементов ограниченной числовой последовательности , то интервал содержится в интервале .

• Справедлива теорема Больцано — Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

Бесконечно большие и бесконечно малые последовательности

• Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

• Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

Свойства бесконечно малых последовательностей

Бесконечно малые последовательности отличаются целым рядом замечательных свойств, которые активно используются в математическом анализе, а также в смежных с ним и более общих дисциплинах.

• Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

• Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

• Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

• Любая бесконечно малая последовательность ограничена.

• Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

• Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.

• Если (x_n) — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность (1 / x_n), которая является бесконечно малой. Если же (x_n) всё же содержит нулевые элементы, то последовательность (1 / x_n) всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно малой.

• Если (α_n) — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность (1 / α_n), которая является бесконечно большой. Если же (α_n) всё же содержит нулевые элементы, то последовательность (1 / α_n) всё равно может быть определена, начиная с некоторого номера n, и всё равно будет бесконечно большой.