Числовой ряд
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
-
вещественные числовые ряды — изучаются в математическом анализе;
-
комплексные числовые ряды — изучаются в комплексном анализе;
Важнейший вопрос исследования числовых рядов — это сходимость числовых рядов.
Числовые ряды применяются в качестве системы приближений к числам.
|
Содержание
|
Определение
Пусть
—
числовая
последовательность; рассмотрим
наравне с данной последовательностью
последовательность
каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида
Вообще, для обозначения ряда используется символ
поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.
В соответствии с этим говорится о сходимости числового ряда:
-
числовой ряд сходится, если сходится последовательность его частичных сумм;
-
числовой ряд расходится, если расходится последовательность его частичных сумм.
Если числовой ряд сходится, то предел S последовательности его частичных сумм носит название суммы ряда:
Операции над рядами
Пусть заданы сходящиеся ряды
и
.
Тогда:
-
Их суммой называется ряд
-
Их произведением по Коши называется ряд
,
где
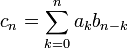
Если оба ряда сходятся, то их сумма сходится, если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.
Критерий абсолютной сходимости
Ряд
сходится
абсолютно тогда и только тогда, когда
сходятся оба положительных ряда
и
Где
Доказательство. Если сходится
то
по признаку
сравнения тем более сходятся
и
Наоборот,
если сходятся
и
то
сходится и их сумма
«O» большое и «o» малое
«O» большое и «o» малое (O и o) — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также при оценке сложности алгоритмов. В частности, фраза «сложность алгоритма есть O(n!)» означает, что при больших n время работы алгоритма (или общее количество операций) не более чем C · n!, где C — некая положительная константа (обычно в качестве параметра n берут объём входной информации алгоритма).
|
Содержание
|