1. Магазинні автомати

Означення. Магазинний автомат — це сімка ,

де: — множина станів магазинного автомату;

— основний алфавіт;

— допоміжний алфавіт (алфавіт магазина);

— початковий стан магазинного автомату;

— початковий вміст магазину;

;

— множина заключних станів автомата .

Поточний стан магазинного автомата описується конфігурацією. Конфігурація магазинного автомата — це трійка , де . Серед конфігурацій магазинного автомата виділимо дві:

• початкова конфігурація , де , — вхідне слово (),

;

• заключна конфігурація , 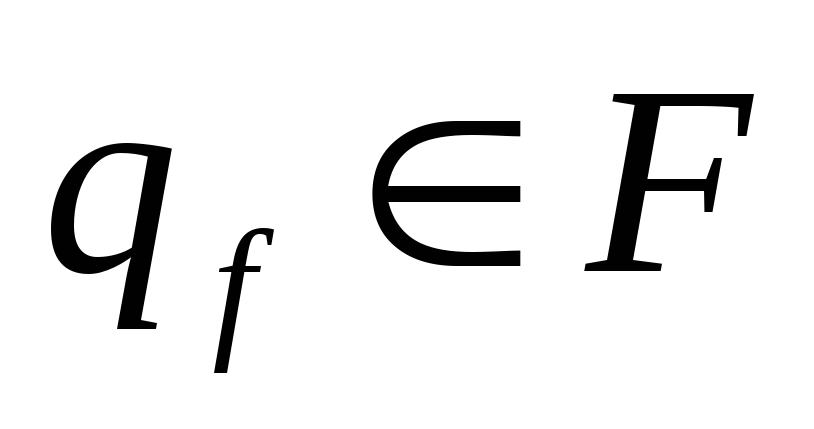. В загальній теорії магазинних автоматів іноді як заключну конфігурацію розглядають , де - фіксована пара. Легко довести, що визначення заключної конфігурації виду не зменшує потужності класу магазинних автоматів.

Такт роботи (позначається ╞═ ) магазинного автомата — це перехід від однієї конфігурації до іншої, а точніше:

╞═ при умові, що .

Робота магазинного автомата (позначається ╞═^*) — це послідовність тактів роботи, а точніше: ╞═^* тоді і тільки тоді, коли ╞═ , ╞═ ,…, ╞═ .

Операції ╞═ та ╞═^* можна трактувати як бінарні відношення на відповідних кортежах. Тоді робота магазинного автомата — це рефлексивно-транзитивне замикання бінарного відношення ╞═.

Означення. Мова, яку розпізнає магазинний автомат (позначається ) - це множина ланцюжків, які задовольняють умові:

╞═^* .

Зафіксуємо наступні результати теорії магазинних автоматів:

1. Не існує алгоритму перетворення недетермінованого магазинного автомата у еквівалентний йому детермінований магазинний автомат.

2. Існує алгоритм, який вирішує проблему порожньої множини для конкретного магазинного автомата.

3. Існує алгоритм, який за час, пропорційний перевіряє, чи належить мові, яку розпізнає магазинний автомат .

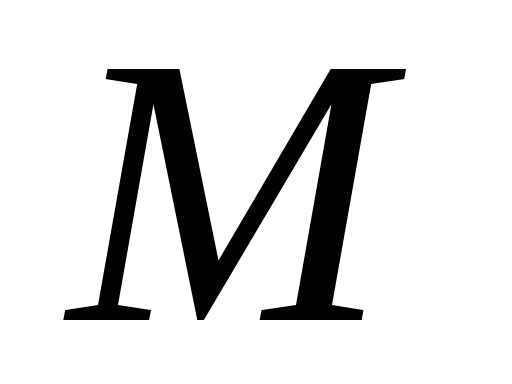4. Клас мов, які розпізнаються магазинними автоматами, співпадає з класом мов, що породжуються КС-граматиками.

На основі сформульованих вище результатів для лівосторонньої стратегії виводу в запропонуємо наступне твердження: для довільної КС-граматики можна побудувати магазинний автомат такий, що . При цьому автомат буде моделювати лівосторонню стратегію виводу в .

Нехай — КС-граматика. Побудуємо відповідний МП-автомат :

• — множину станів автомата складає один стан ;

• — допоміжний алфавіт;

• — початковий вміст магазина.

• функцію визначимо так:

• якщо належить 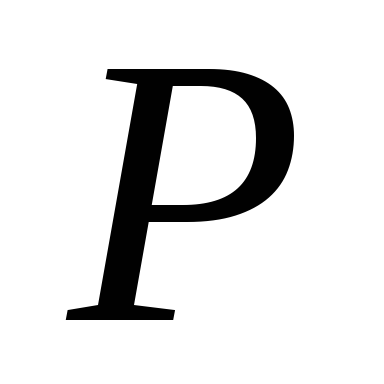, то

.

• також поповнимо множину значень функції наступними значеннями:

.

Для ланцюжка , покажемо, якщо ми за кроків безпосереднього виводу , то відповідний автомат за кроків допустить . Зробимо перший крок безпосереднього виведення тоді МП-автомат з початкової конфігурації перейде в наступну конфігурацію . Далі розглянемо наступні ситуації:

• коли — термінал (тобто ), тоді МП-автомат виконає наступний такт: ╞═ ;

• коли — нетермінал, тоді в схемі 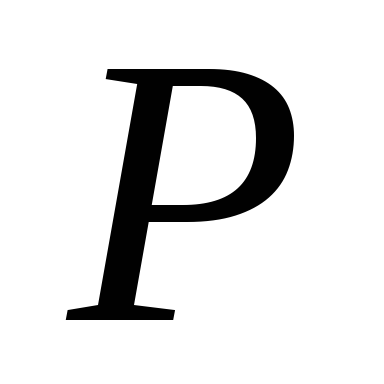граматики виберемо правило виду , зробимо наступний крок безпосереднього виведення : . При таких умовах автомат перейде в наступну конфігурацію: ╞═ .

Очевидно, якщо ланцюжок виводиться за кроків, то МП-автомат зробить кроків та розпізнає . Таким чином, .