54

1. Задача 1

"Исследование напряженно-деформированного состояния

в точке тела"

Цель решения этой задачи – усвоение основ теории напряжений и деформаций.

Полагаем, что напряженно-деформированное состояние тела было определено расчетами или экспериментально.

1.1. Напряженное состояние в точке тела

Мысленно вырежем в окрестности произвольной точки нагруженного тела элементарный (бесконечно малый) параллелепипед, грани которого перпендикулярны координатным осям .

Условие задачи. Компоненты напряжений, действующие по граням параллелепипеда, равны следующим величинам:

(1.1)

Э

Рис. 1

ти компоненты напряженного состояния показаны на рис. 1 с учетом правила знаков, принятого в теории упругости (см. первую часть учебного пособия, стр. 6).

Совокупность нормальных и касательных напряжений на трех взаимно перпендикулярных площадках

называют тензором напряжений.

Напряженное состояние (НС) в точке полностью определено, если известны шесть компонентов тензора напряжений (см. рис. 1), т. е., зная эти шесть компонентов напряжений в точке, можно вычислить напряжения на любой площадке, проходящий через эту точку.

1.1.1. Полное, нормальное и касательные напряжения на наклонной площадке

Найдем напряжения на некоторой наклонной к осям площадке, проходящей через заданную точку. Положение площадки относительно осей координат определяется направляющими косинусами внешней нормали к этой площадке. Вначале вычисляем значения проекций на оси координат полного напряжения по формулам:

(1.2)

Затем находим величину полного напряжения:

(1.3)

Зная проекции , полного напряжения, действующего по наклонной площадке, можно определить нормальное и касательное напряжения по формулам:

(1.4)

(1.5)

Р

Рис. 2

ассмотрим применение формул (1.2)-(1.5), используя исходные данные (1.1).

Пусть положение внешней нормали к площадке (рис. 2) относительно координатных осей определено следующими значениями направляющих косинусов (табл. 1.2 первой части учебного пособия):

Полезно проверить правильность величин направляющих косинусов подстановкой их в выражение

(1.6)

которое должно превращаться в тождество.

Подставляя значения напряжений и направляющих косинусов в формулы (1.3), получим:

(1.7)

С

Рис. 3

оставляющие полного напряжения и, имеющие знак минус, противоположны направлениям осей и . Положительная составляющая направлена вдоль положительной оси y (см. рис.2).

Значения , и , вычисленные по формулам (1.3)–(1.5) с учетом заданных напряжений (1.1) и направляющих косинусов, имеют следующие значения:

Напряжение имеет знак плюс. Следовательно, оно будет направлено от сечения (рис. 3).

1.1.2. Вычисление проекции касательного напряжения на заданное направление

Направление касательного напряжения в плоскости сечения с внешней нормалью относительно любых двух ортогональных осей и , лежащих в той же плоскости определяется следующим образом.

Вначале определяются проекции полного напряжения на оси и в виде и (рис. 4).

З

Рис. 4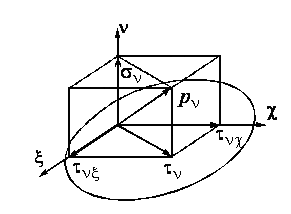

атем угол между касательным напряжением и, например, осью найдем по формуле

Напомним, как найти, например, – проекцию полного напряжения на ось . Обозначим направляющие косинусы оси , как , и спроектируем на ось :

(1.8)

Подставляя в (1.8) вместо их значения в виде (1.2), получим

(1.9)

Здесь – направляющие косинусы внешней нормали к площадке, по которой действует касательное напряжение .

Рассмотрим вновь трехгранную призму, показанную на рис. 3. Найдём проекцию касательного напряжения , действующую по площадке ВСК, на ось , т.е. касательное напряжение (см. рис. 3).

Внешняя нормаль к площадке ВСК совпадает с положительной осью и её направляющие косинусы

(1.10)

Направляющие косинусы оси имеют следующие значения:

(1.11)

Вычислим касательное напряжение по формуле (1.9) с учётом (1.1), (1.10) и (1.11):

Поскольку внешняя нормаль к площадке совпадает с положительной осью , то отрицательное касательное напряжение будет направлено в сторону, противоположную направлению оси (см. рис. 3).