6.3. Резонансно-туннельный диод (ртд)

Резонансно-туннельным диодом будем называть многослойную полупроводниковую структуру, в которой имеется ДБКС, параметры которой подбираются таким образом, чтобы в КЯ имелся один резонансный уровень.

6.3.1. Строение и действие ртд

Рис. 6.10. Схема РТД на основе гетероструктуры GaAs / Al_x Ga_1-x As

с одним резонансным уровнем в КЯ.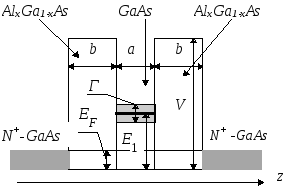

На рис.6.10 представлена схема резонансно-туннельного диода на основе гетероструктуры GaAs / Al_x Ga_1-x As, состоящего из пяти слоев, крайние из которых обычно представляют собой сильно легированный GaAs с вырожденным электронным газом. Барьеры ДБКС состоят из нелегированного твердого раствора Al_x Ga_1-x As . В КЯ из собственного GaAs находится один резонансный уровень E₁ с уширением Г: при х=0.3, V  0.2 эВ, а=5 нм, b=25 нм, Е₁  7080 мэВ, Г=Г_b 230 мэВ (см. табл.3), ( ( 77 К )  0.1 мэВ , ( 300 К ) 2 мэВ ).

Если к такой структуре приложить разность потенциалов, то через нее пойдет ток, имеющий две составляющие - резонансную и нерезонансную. Резонансный ток связан с движением электронов от эмиттера до коллектора через резонансный уровень в КЯ, положение которого в данном случае является функцией приложенного напряжения U. Нерезонансная составляющая связана прежде всего с надбарьерным протеканием и нерезонансным подбарьерным. Очевидно, с понижением температуры и улучшением параметров ДБКС (увеличением вероятности резонансного туннелирования и уменьшением нерезонансного) нерезонансная составляющая будет убывать.

Чтобы получить качественную картину зависимости резонансной составляющей тока симметричного РТД от напряжения, для простоты будем считать, что электронный газ в эмиттере и коллекторе является вырожденным и характеризуется энергией Ферми Е_F. Тогда положение резонансного уровня с учетом (6.43) будет выражаться через приложенную разность потенциалов формулой (рис.6.11)

Рис. 6.11. Схема протекания тока в симметричном РТД.

. (6.57)

Е

Рис. 6.12. Сфера заполненных вырожденным электронным газом состояний

в зоне Бриллюэна с радиусом k_F -сфера Ферми.

сли , то, очевидно, резонансный ток равняется нулю (). С увеличением приложенного напряжения резонансный уровень энергии понижается и при резонансный ток становится отличным от нуля. При дальнейшем росте напряжения резонансная составляющая тока должна расти, так как при этом уменьшается значение и увеличивается число электронов в сфере Ферми с волновым числом (см. рис. 6.12), которые могут туннелировать через резонансный уровень. Из этого рисунка при условии

следует, что число электронов, с заданным значением q и энергией движения вдоль оси симметрии РТД пропорционально площади сечения сферы Ферми, равной . При резонансный ток с увеличением напряжения быстро уменьшается и становится равным нулю, потому что резонансный уровень энергии при этом попадает в запрещенную зону⁷. Как показывает численный анализ, при вольтамперная характеристика РТД имеет максимальную отрицательную дифференциальную проводимость.