5.3. Вертикальный перенос в сверхрешетках
Как отмечалось
ранее, перенос носителей заряда в СР
может осуществляться не только вдоль
КЯ (латеральный перенос), но и поперек
(вертикальный перенос) за счет
туннелирования электронов и дырок через
потенциальные барьеры, отделяющие одну
КЯ от другой. Латеральный перенос в СР
в основном является аналогичным переносу
в изолированной КЯ. В одноминизонном
приближении и приближении двумерного
электронного газа (
)
все формулы, полученные ранее для
переноса носителей заряда в КЯ, справедливы
и для латерального переноса в СР. При
этом нужно заменить поверхностную
концентрацию носителей
на объемную
,
двумерную плотность состояний
на объемную
.
5.3.1. Область омической проводимости
Для вертикального переноса в СР из слабо взаимодействующих КЯ формула (5.7) для неравновесной добавки к функции распределения преобразуется к виду
, (5.17)
где вместо
стоит выражение, полученное с учетом
(2.35) для скорости носителей заряда вдоль
оси симметрии СР
.
(5.18)
Зависимость времени релаксации от энергии и температуры с учетом того, что носители заряда при вертикальном переносе основное время проводят в КЯ, имеет тот же вид, что и при планарном переносе
.
(5.19)
С учетом (5.17) удельную проводимость, описывающую вертикальный перенос в области слабых классических полей, рассчитанную по формуле (5.6), можно представить в виде
, (5.20)
где
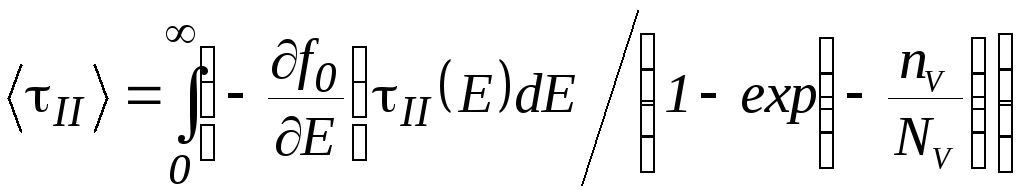(5.21)
– усредненное по энергии время релаксации носителей заряда при вертикальном переносе;
(5.22)
– усредненное по
энергии значение обратной эффективной
массы, связанной с движением вдоль оси
СР,
– эффективная масса электронов на дне
минизоны, определяемая формулой (2.37);
– эффективная плотность состояний в
нижней минизоне.
Для невырожденного
газа носителей заряда (
)
усредненное время релаксации, рассчитанное
по формуле (5.21), и среднее значение
обратной эффективной массы равны
,
(5.23)
.
(5.24)
С учетом
одноминизонного приближения (
)
из формулы (5.24) следует, что
,
т.е. среднее значение эффективной массы
носителей заряда при вертикальном
переносе много меньше эффективной массы
на дне минизоны и прямо пропорционально
температуре. Отсюда следует, что
подвижность носителей заряда в СР при
вертикальном переносе много меньше,
чем при планарном за счет увеличения
эффективной массы.
Для зависимости подвижности невырожденного газа при вертикальном переносе от температуры с учетом формул (5.23) и (5.24) получаем
.
(5.25)
Для вырожденного
газа носителей заряда (
)
из формул (5.21) и (5.22) следует
,
(5.26)
.
(5.27)
Для вертикальной подвижности и проводимости с учетом полученных формул имеем
, (5.28)
. (5.29)
В случае промежуточного вырождения носителей заряда зависимость вертикальной проводимости от концентрации согласно (5.20)-(5.22) носит экспоненциальный характер
.
(5.30)
С ростом концентрации экспоненциальный рост вертикальной проводимости в области полного вырождения сменяется областью насыщения, в которой зависимость проводимости от концентрации и температуры определяется формулой (5.29).