3.2. Сверхрешетки

Для сверхрешеток из КЯ, с учетом формулы (2.29) для энергетического спектра, формула (2.27) для числа разрешенных состояний в минизоне с энергией меньше E после несложных преобразований принимает вид

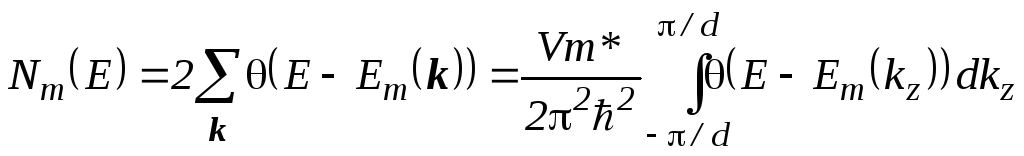, (3.16)

где –объем СР, состоящей из N периодов величиной d с площадью слоя S. Расчет по этой формуле предполагает знание дисперсии энергии в минизоне, которая определяется из решения уравнения (2.2) с периодической функцией потенциальной энергии. В предельном случае слабо взаимодействующих КЯ (см. (2.34)), что соответствует ширине минизон близкой к нулю (), формула (3.16) переходит в формулу (3.5) умноженную на число периодов СР, равное числу КЯ:

. (3.17)

Для объемной плотности состояний в предельном случае получаем формулу аналогичную (3.6)

, (3.18)

где 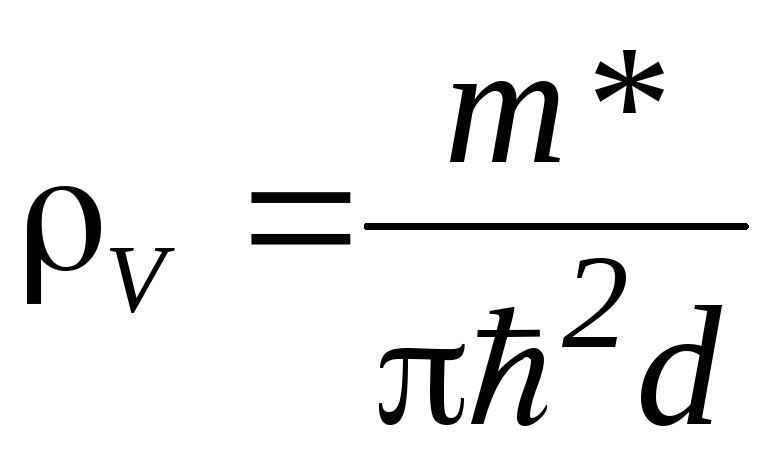(3.19)

–объемная (трехмерная) плотность состояний в минизоне КЯ, не зависящая от энергии и номера минизоны. На рис. 3.3 представлена зависимость плотности состояний СР от энергии в окрестности дна зоны проводимости (вершины валентной зоны) в предельном случае и в случае . Из рисунка следует, что при наличие взаимодействия между КЯ форма ступенек плотности состояний изменяется. Вместо скачка при подключении более высокой минизоны происходит непрерывный переход в пределах ширины этой минизоны. Очевидно, что с ростом взаимодействия между КЯ форма кривой плотности состояний непрерывно будет переходить в кривую плотности состояний объемного полупров

Рис. 3.3. Зависимость плотности состояний СР от энергии

в окрестности дна зоны проводимости (вершины валентной зоны):

а) ; б) ; с) трехмерная плотность.

одника.

Для объемной концентрации носителей заряда в СР из слабо взаимодействующих КЯ в одноминизонном приближении получается формула, аналогичная (3.10), в которой следует заменить на , а на :

. (3.20)

В предельных случаях вырождения из (3.20) получаются формулы, аналогичные (3.11).

4. Оптические свойства

Основными характеристиками оптических свойств полупроводников и структур на их основе является дисперсия комплексного показателя преломления N, как функции частоты или длины волны света [16]. В изотропном случае распространение света вдоль оси x связано с комплексным показателем преломления формулой

, (4.1)

где F–световой вектор¹⁵, , –вещественный показатель преломления, –показатель поглощения. Так как плотность энергии света пропорциональна квадрату модуля светового вектора, ее зависимость от координаты в поглощающей среде с учетом (4.1) определяется формулой

, (4.2)

где

(4.3)

–коэффициент поглощения. В общем случае коэффициент поглощения представляет собой аддитивную функцию, отдельные члены которой соответствуют поглощению света различными частицами или квазичастицами, которые входят в состав данной среды.

В полупроводниках основным видом поглощения является поглощение света на электронах¹⁶. Дисперсия коэффициента поглощения определяется энергетическим спектром и волновыми функциями электронов и дырок в рассматриваемой области частот. Согласно квантовой механике [17] поглощение света электронами в первом приближении теории возмущений происходит в результате оптических переходов электронов из состояний с меньшей в состояния с большей энергией. Таких переходов существует два вида–прямые, при которых выполняется закон сохранения квазиимпульса, и непрямые. Вероятность последних, а следовательно и значение коэффициента поглощения, связанного с ними, существенно меньше. Причиной этого является то, что при прямых переходах происходит взаимодействие электрона и фотона, а непрямые переходы предполагают взаимодействие их с третьей квазичастицей¹⁷.