3. Плотность состояний и концентрация носителей заряда

Как известно, большинство электрических и оптических свойств полупроводников зависит от концентрации свободных носителей заряда n. В свою очередь равновесная концентрация при заданной температуре и степени легирования зависит от энергетического спектра, а точнее, как и многие другие физические величины, от плотности состояний :

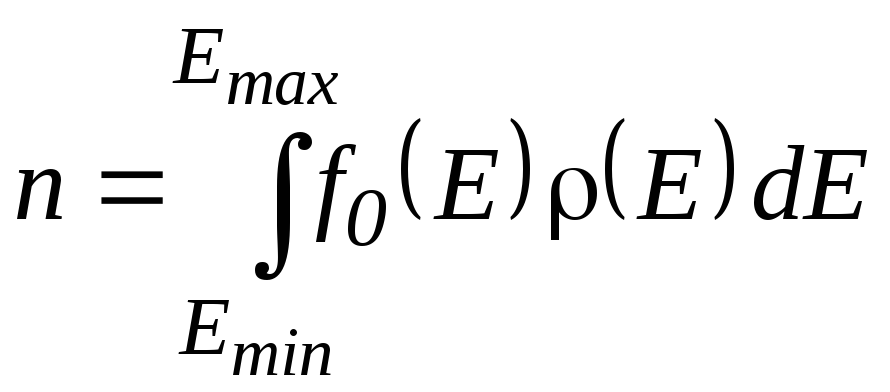, (3.1)

где –равновесная функция Ферми-Дирака, F–уровень Ферми. Функция плотности состояний–число разрешенных состояний с энергией от E до E+dE, рассчитанное на единицу энергии. Если известно число состояний с энергией от до E, функцию плотности состояний можно рассчитать по формуле

. (3.2)

Согласно определению

, (3.3)

–функция Хевисайда, равная нулю при x<0 и равная 1 при x>0; m–полный набор квантовых чисел, определяющих состояние с данной энергией, с учетом спиновых составляющих.

3.1. Изолированные квантовые ямы и нити

С учетом (2.8) формула для функции в изолированной КЯ принимает вид

, (3.4)

где –число разрешенных состояний в подзоне номера m с энергией от до E:

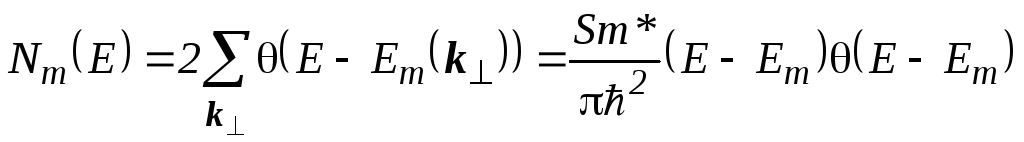. (3.5)

Формула получена с помощью перехода от суммирования по к интегрированию. Фактор 2 перед суммой учитывает наличие у электрона спина. С учетом (3.2) для плотности состояний, рассчитанной на единицу площади слоя КЯ, получаем

, (3.6)

где (3.7)

–

Рис. 3.1. Зависимость поверхностной плотности состояний в изолированной КЯ от энергии в окрестности дна зоны проводимости (вершины валентной зоны).

поверхностная (двумерная) плотность состояний в двумерной подзоне КЯ, не зависящая от энергии и номера подзоны. На рис. 3.1 представлена ступенчатая зависимость двумерной плотности состояний от энергии, определяемая формулой (3.6). Характерной особенностью этой зависимости является одинаковая высота ступенек, имеющая место в приближении¹⁴ независимости m* от номера подзоны.

С учетом формул (3.1) и (3.6), для поверхностной концентрации носителей заряда имеем

, (3.8)

где

(3.9)

–поверхностная концентрация в подзоне с номером m, –эффективная плотность состояний в подзоне. В одноподзонном приближении, когда носители заряда в основном находятся в нижней подзоне ()

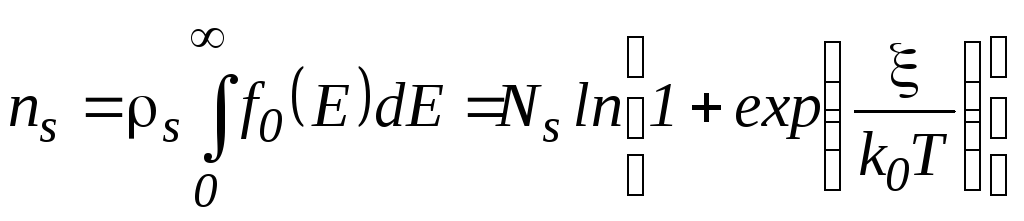, (3.10)

где –приведенный уровень Ферми. Для предельных случаев невырожденного газа носителей заряда и вырожденного из формулы (3.10) для поверхностной концентрации в одноподзонном приближении получаем

. (3.11)

Формула (3.11) аналогична формуле для концентрации невырожденных электронов в трехмерных структурах, если в ней заменить трехмерную объемную плотность состояний на двумерную поверхностную.

Для квантовых нитей формула (3.5) с учетом (2.20) принимает следующий вид

, (3.12)

где –длина КН. Для плотности состояний, рассчитанной на единицу длину КН–линейная плотность состояний–из формулы (3.2) с учетом (3.3) и (3.12) получаем

. (3.13)

На рис. 3.2 представлена качественная зависимость функции для изолированной КН. Из рисунка следует, что эта плотность состояний является аналогом плотности состояний трехмерных структур в однородном магнитном поле. Отличительной особенностью от трехмерного случая является отсутствие периодической зависимости в чередовании пиков, наличие которой в объемных полупроводниках определяется эквидистантным характером уровней Ландау.

Рис. 3.2. Зависимость линейной плотности состояний в изолированной КН

от энергии в окрестности дна зоны проводимости (вершины валентной зоны).

Для линейной концентрации носителей заряда с учетом (3.1) и (3.13) после несложных преобразований получаем

. (3.14)

В одноподзонном приближении для предельных случаев вырождения из формулы (3.14) следует

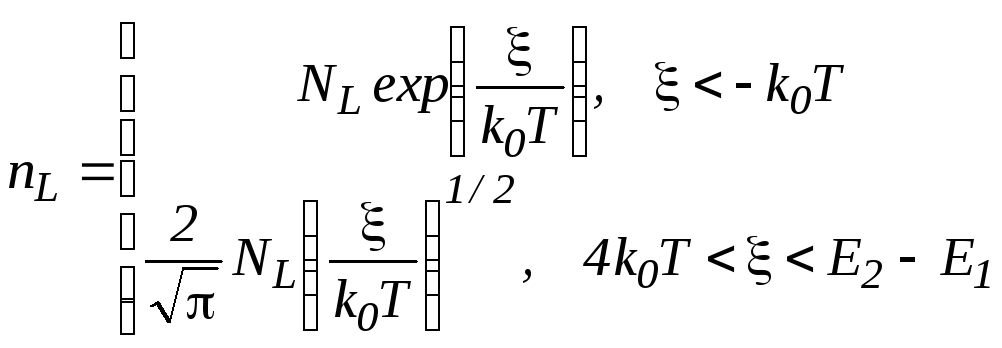. (3.15)

где – линейная эффективная плотность состояний в подзоне КН.