3. Задачи для самостоятельного решения

Доказать, что следующие функции не являются дифференцируемыми ни в одной точке: а) Im z , б), где - аналитическая функция.

При каких дифференцируемы следующие функции: а) , б), в), г).

Исследовать на аналитичность функции:

а)	б)
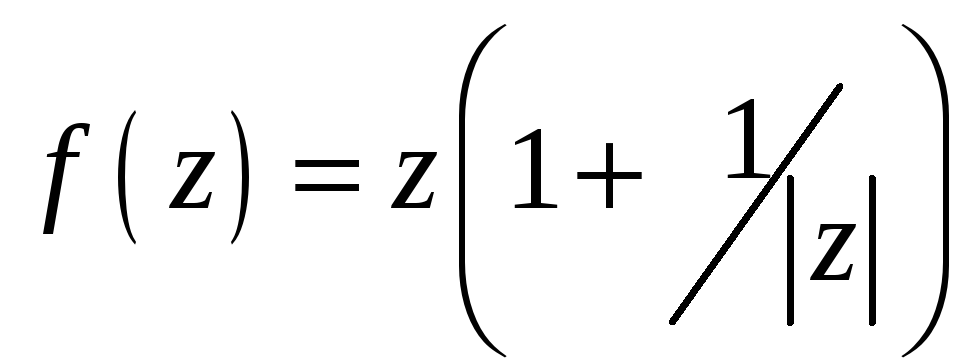
в)	г)
д)	е)
ж)	з)
и)	к)
л)	м)

Найти области аналитичности и доказать формулы

; ; ; ;;;

Найти аналитическую функцию, если

а); б);

в) .

г);

д).

4. Интегрирование функций комплексного переменного

Напомним, что областью называется множество точек комплексной плоскости, обладающее свойствами: 1) состоит из одних внутренних точек (свойство открытости); 2) любые две точки, принадлежащие, можно соединить непрерывной линией, целиком состоящей из точек (свойство связности).

Кривая заданная уравнениями

называется гладкой, если функции и непрерывны и имеют непрерывные первые производные, не обращающиеся в нуль одновременно. Непрерывная кривая, составленная из конечного числа гладких кривых, называется кусочно-гладкой.

В комплексной плоскости кривая (4.1) задается уравнением.

1. Вычисление интегралов. Теорема Коши. Интегральная формула Коши

Пусть в области задана непрерывная функция и кусочно-гладкая кривая. Тогда

Интеграл от функции комплексного переменного вдоль кривой можно свести к определенному интегралу. Пусть– гладкая кривая, для которой дано параметрическое представление, и на, тогда

где и - начальная и конечные точки кривой.

Теорема 4.20 (Коши). Если - односвязная область в  и - аналитическая в этой области функция, то для любого контура

(контур – кусочно-гладкая жорданова замкнутая кривая).

Теорема 4.21 (Коши для многосвязной области). Пусть– контуры, лежащие внутри контура, причем каждая кривая лежит вовне любой другой кривой .

Если многосвязная область ограничена контурами, а функция – аналитическая в и непрерывна в, то.

Формула Ньютона-Лейбница. Если функция аналитическая в односвязной области и точки и принадлежат этой области, то справедлива формула Ньютона-Лейбница

.

Интегральная формула Коши. Пусть– аналитическая в области функция, а–контур, принадлежащий вместе со своей внутренностью, тогда для любой точки, лежащей внутри контура, справедлива формула

(4.6)

Аналитическая в области функция имеет во внутренних точках области производную любого порядка и справедлива формула для производных

,

причем контур и точка удовлетворяют тем же условиям, что и в интегральной формуле Коши.

2. Примеры с решениями

Пример 4.1. Вычислить, где – дуга параболы от точки до точки. (Рис.12)

Рис. 12. Путь интегрирования к примеру 4.1

Рис. 13. График к примеру 4.3.

Решение. На комплексной плоскости точкам и отвечают точки и. Как мы знаем (см. пример 3.1 части 1) подынтегральная функция не является аналитической ни в одной точке комплексной плоскости, поэтому для вычисления интеграла нельзя применять формулы для аналитических функций. Воспользуемся формулой (4.2). Имеем

Пример 4.2. Вычислить интеграл, где – дуга параболы от точки до точки.

Решение. Также как в предыдущем примере подынтегральная функция не аналитическая. На этот раз применим формулу (4.3). Для этого введем параметр, полагая

Комплексное уравнение параболы. Тогда, в силу формулы (4.3), имеем.

Пример 4.3. Вычислить где дуга окружности от точки до точки (Рис.13).

Решение. Кривая интегрирования полностью лежит в области аналитичности подынтегральной функции, поэтому результат интегрирования не зависит от кривой, соединяющей точки и, и применима формула Ньютона-Лейбница (4.5). Имеем

Пример 4.4. Вычислить интеграл.

Решение. Данный интеграл типа Коши представим в виде, где. Поскольку функция является аналитической внутри единичного круга, то в силу формулы (4.6) имеем.

Пример 4.5. Вычислить где контур.

Решение. Здесь контур интегрирования обладает тем свойством, что сумма расстояний от точки контура до двух точек есть постоянная величина, равная 4. Как известно это эллипс с фокусами, расположенными в точках и, с большей полуосью. Точка же лежит на действительной оси и не принадлежит внутренности контура, следовательно, подынтегральная функция – аналитическая в замкнутой области, ограниченной данным контуром. Согласно теореме Коши

Пример 4.6. Вычислить

Решение. Подынтегральная функция аналитическая, поэтому можно воспользоваться формулой интегрирования по частям. Имеем