Кинетическая энергия твёрдого тела.

Перейдём к вычислению кинетической энергии твердого тела. Формула для кинетической энергии i-той точки хорошо известна , для системы точек она равна , а для вёрдого тела её можно записать .

Подставим в эту формулу скорость точки твердого тела, выражаемую первой формулой (70); после некоторых про­стых преобразований получим

(80)

Для вычисления последнего интеграла произведем пре­образование подынтегрального выражения, рассматривая его как скалярно-векторное произведение трех векторов: и ; произведя круговую перестановку сомножителей в нём и раскрывая появляющееся при этом двойное вектор­ное произведение, используем далее единичный тензор и формулу (50), имеем

Подставляя этот результат в формулу (80), находим окончательное выражение для кинетической энергии твердого тела в общем случае его движения.

Если за полюс принят центр инерции твердого тела, то формула (52) упрощается:

(81)

В качестве осей координат возьмем связанные с самим движущимся твердым телом его главные централь­ные оси инерции; тогда выражение (81) в развернутом виде будет выглядеть так:

Если твердое тело вращается вокруг неподвижной точки, то, помещая полюс в эту неподвижную точку, имеем ; обозначая затем эту неподвижную точку через О, получим из общей формулы (80) следующее простое выражение .

Дифференциальные уравнения движения твердого тела

В кинематике была получена формула, связывающая абсолютную и относительную производные переменного вектора

(82)

Напомним, что здесь - абсолютная производная, вы­деляемая неподвижным наблюдателем; - относительная производная, вычисляемая подвижным наблюдателем; - угловая скорость подвижного наблюдателя.

Перейдем к составлению уравнений движения твер­дого тела, вращающегося вокруг неподвижной точки О.

Кинетический момент твердого тела в этом случае вы­ражается формулой

(Свяжем систему осей Oxyz с вращающимся телом и воспользуемся теоремой об изменении кинетического момента с учётом формулы (82)

(83)

Тензор инерции твердого тела в осях, связанных с самим телом, будет постоянным, поэтому относительная производная его будет , и выражение (83) следует записать в виде

(84)

Тогда векторное уравнение вращения твердого тела вокруг не­подвижной точки будет иметь вид

(85)

Предполагая оси х, у, z главными, имеем

Проекции уравнения (85) на оси, связанные с телом, будут

(86)

Уравнения (86) называются динамическими уравнениями Эйлера.

Перейдем теперь к общему случаю движения свободного твердого тела в пространстве, которое всегда можно разбить на два более простых движения: поступательное движение вместе с произвольно выбранным полюсом и вращательное движение вокруг этого полюса. Такому представлению движения твердого тела соответствуют и уравнения движения, которые распадаются на уравнения движения полюса и урав­нения вращения твердого тела.

Уравнения движения полюса получим, используя теорему об изменении количества движения системы , здесь — главный вектор внешних сил, приложенных к твёрдому телу, а количество движения твердого тела определяется формулой

(91)

где М - масса твердого тела; v_A, v_c — скорости полюса и центра инерции тела; —его угловая скорость, а —радиус-вектор, проведенный из полюса А в центр инерции тела С.

Подстановка количества движения твердого тела (91) в теорему об изменении количества движения дает

(92)

Поскольку, как уже указывалось, удобнее составлять уравнения движения в осях, связанных с твердым телом, необходимо абсолютные производные, стоящие в соотношении (92), выразить по формуле (82) через относительные; тогда

(93)

Здесь уже принято во внимание, что , так как для наблюдателя, связанного с твердым телом, вектор постоянен. Подставив формулы (93) в уравнение (92), получим

(94)

Уравнение (94)- дифференциальное уравнение движения полюса А эквивалентно трем уравнениям в проекциях на оси х, у, z, связанные с телом; проектируя его, например, на ось х, имеем:

⁽⁹⁵⁾

Остальные два уравнения (в проекциях на оси у и z) по­лучаются из уравнения (95) круговой перестановкой индек­сов.

Переходим к выводу дифференциального уравнения вра­щения твердого тела вокруг полюса А. Для этого в теорему об изменении кинетического момента следует подставить общее выражение кинети­ческого момента (73), которое в данной ситуации вы­годнее представить так:

(96)

Беря абсолютные производные по времени, находим

(97)

В правой части уравнения (97) совершен известный пе­реход от главного момента относительно точки О к главному моменту относительно точки А (полюса); при этом первые слагаемые в левой и правой частях сокращаются. Учитывая далее формулы (91), (93), преобра­зуем уравнение (97) к следующему виду:

(98)

Но первое слагаемое в полученном соотношении тождественно равно нулю, а второе и третье - сокра­щаются, поэтому уравнение вращения твердого тела вокруг полюса А примет такой вид:

(99)

Уравнение (99) эквивалентно трем уравнениям в проек­циях на оси х, у, z, связанные с твердым телом; проекция его на ось х будет выглядеть так (напоминаем, что оси х, у, z – главные оси инерции в точке А

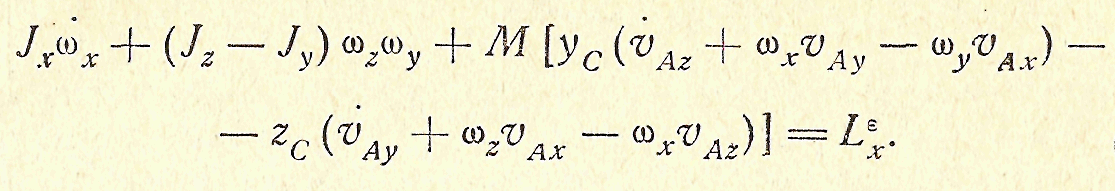⁽¹⁰⁰⁾

Остальные два уравнения (проекции на оси x и y ) можно получить из уравнения (100) круговой перестановкой индексов. Если полюс А поместить в центр инерции тела С, то и уравнения (94) и (99) существенно упрощаются; в этом случае имеем

; (101)

Именно эти уравнения обычно употребляются при изучении движения твёрдого тела в пространстве (самолёт, подводная лодка и т.д.).