Динамика системы материальных точек

Предварительные замечания об общих теоремах динамики. Задача об интегрировании дифференциальных уравнений движения материальной точки, представляющая даже в случае одной точки некоторые трудности, становится подчас непосиль­ной, когда приходится иметь дело с движением системы мате­риальных точек. Силы, приложенные к отдельным точкам си­стемы, могут зависеть от положения и движения остальных точек системы, так что правые части дифференциальных урав­нений, написанных для каждой точки в отдельности, будут со­держать время, координаты и проекции скорости всех точек системы. В результате вопрос сводится к интегрированию си­стемы дифференциальных уравнений.

Но иногда оказывается достаточным опреде­лить изменение некоторых суммарных мер движения системы в целом (количества движения, момента количества движения, кинетической энергии) в зависимости от суммарных мер дейст­вия сил (главный вектор и главный момент приложенных сил, работа сил, потенциальная энергия). Такого рода соотношения между изменениями во времени суммарных мер движения системы материальных точек и сум­марными мерами действия приложенных к точкам совокупности сил выражают общие теоремы динамики системы материальных точек, применяемые как для отдельных точек и их систем, так и для сплошных сред. К числу общих теорем динамики относятся: теорема об изме­нении количества движения с ее модификациями - теоремой импульсов и теоремой о движении центра масс, теорема об из­менении момента количеств движения, а также теорема об изменении кинетической энергии.

В основе вывода первых двух общих теорем динамики- ко­личества движения и момента количества движения- лежит идея выделения из всех сил, приложенных к системе, внутренних сил взаимодействия между материальными точками системы. Внутренние силы в своей совокупности не могут влиять на такие суммарные меры движения, как главный вектор и главный мо­мент количеств движения точек системы. Только внешние силы, действующие на точки системы со стороны внешних тел, не при­надлежащих к рассматриваемой системе, могут изменять глав­ный вектор и главный момент количеств движения системы. В использовании этого свойства внутренних сил, представляю­щего собой одно из важнейших следствий третьего закона Ньютона, заключается главное значение двух первых общих теорем динамики. Рассмотрим систему, состоящую из n точек. На каждую из них действуют силы со стороны других точек (рис. 52), причём и . На каждую точку системы действует равнодействующая , но сумма всех равнодействующих ,

где - главный вектор всех внутренних сил. Нетрудно увидеть, что и сумма моментов всех внутренних сил, независимо от выбора центра, также будет равен нулю. Итак, главный вектор и главный момент всех внутренних сил, действующих на систему точек, равны нулю.

Теорема об изменении кинетической энергии устанавливает связь между изменением основной меры движения системы ма­териальных точек- кинетической энергии и мерой действия сил на протяжении путей движения точек системы - работой сил. Таким образом, в круг вопросов механики вводится понятие энергии. Значение этого понятия состоит в том, что им определяется единая физическая величина, прояв­ляющаяся в различных физических явлениях и, таким образом, связывающая их между собой. Понятие энергии объединяет ме­ханику с термодинамикой, с учением об электрических явле­ниях и т. п. Преобразование механической энергии в другие формы энергии и обратное преобразование этих форм в механи­ческую энергию представляет важную задачу современной техники.

В отличие от изменения количества движения и момента ко­личества движения изменение кинетической энергии материаль­ной системы зависит от работы как внешних, так и внутренних сил. Однако и в этом случае выделение класса внутренних сил оказывается полезным, так как, например, в случае движения абсолютно твердого тела или системы абсолютно твердых тел работа внутренних сил равна нулю, а в случае сплошной среды она позволяет судить о потерях механической энергии за счет внутреннего трения.

Теорема об изменении количества движения системы материальных точек.

Положение системы материальных точек (i = 1, 2,..., п) будем определять вектор-радиусами этих точек относительно неподвижного начала коорди­нат О; скорости и ускорения точек системы обозначим соответственно через , . Тела, не включаемые в рассматриваемую систему, назовем внешними по отношению к системе. Такое разделение тел на входящие в систему и не входящие в нее зависит от способа рассмотрения. Мы можем (и в дальней­шем будем так неодно­кратно поступать) то включать некоторые тела в данную си­стему, то исключать их из этой системы.

Таким образом, силы, приложенные к данной системе, мы разбиваем на две категории:

1) внутренние силы — силы взаи­модействия материальных точек, входящих в данную систему, и 2) внешние силы — силы взаимодействия системы с телами внешними по отношению к системе. Обозначим равнодействующую всех внешних сил, приложен­ных к точке через , а всех внутренних — через тогда дифференциальные уравнения движения системы материальных точек могут быть представлены совокупностью основных урав­нений динамики для отдельных точек системы

(21)

Уравнения (21) образуют систему Зп обыкновенных дифференци­альных уравнений второго порядка с Зп неизвестными величи­нами , которые должны быть определены как функции времени. Начальные условия, необходимые для определения произвольных постоянных интегрирования, представляют сово­купность начальных условий для каждой точки системы в от­дельности. Но, в отличии от формулы (1) мы складываем вектора, приложенные в разных точках системы, и тогда, вспоминая правило Пуансо (см. глава ), должны появиться и пары этих векторов. Для лучшего понимания введём вектор , называется количеством движения точки. Вектор , рав­ный

(22)

называют главным вектором количества движения системы. Складывая вектора количества движения точки, мы должны получить, следуя правилу Пуансо, не только главный вектор количества движения, но и величину

, (23)

называемую главным моментом количества движения или сокращённо кинетическим моментом. Именно эти две величины вместе определяют движение системы материальных точек и, в частности, движение твёрдого тела в самом общем случае. В зависимости от поставленной задачи, в частных случаях, может быть использована одна из этих величин.

Вывод теоремы об изменении количества движения системы, или, как ее кратко называют, теоремы количества движения, основан на идее исключения внутренних сил из дифференциаль­ных уравнений движения системы материальных точек (1).

Пусть на «i» точку системы действуют внешние и внутренние силы. Продифференцируем (22) по времени

Но последняя сумма, как главный вектор внутренних сил, должна равняться нулю, обозначая , где -главный вектор внешних сил, получаем

(24)

Это соотношение выражает теорему об изменении количества движения:

векторная производная по времени от главного вектора количества движения системы равна главному вектору внешних сил, приложенных к системе. Равенство нулю главного вектора внутренних сил приводит к заключению, что внутренние силы не могут влиять на измене­ние количества движения системы.

Если главный вектор внешних сил равен нулю, т. е. система изолирована от воздействий внешних по отношению к ней тел, то количество движения системы будет сохраняться во времени как по величине, так и по направлению. В этом заключается за­кон сохранения количества движения.

Рассмотрим другую формулировку теоремы об изменении количества движения. По некоторой аналогии с понятием о центре тяжести твердого тела введем в рассмотрение точку С с вектор-радиусом

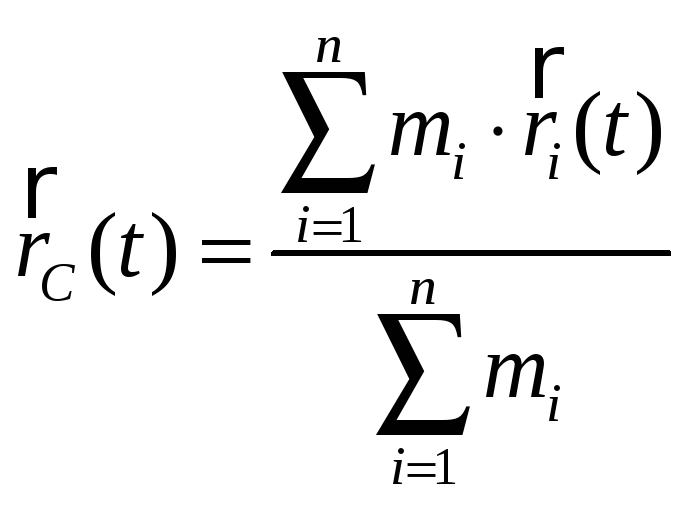(25)

и назовем эту точку центром масс системы материальных точек.

Понятие центра масс является более общим, чем понятие центра тяжести: в отличие от понятия центра тяжести понятие центра масс не связано во-первых с наличием каких- либо сил, а во-вторых вектора и не являются постоянными величинами.

Взяв производную по времени от обеих частей равенства (25), определяющего вектор-радиус центра масс, получим

(26)

где - масса всей системы, откуда следует, что количество движения системы материальных точек равно произведению массы системы на скорость движения ее центра масс, или, иными словами, количеству движения цен­тра масс, в котором предположена сосредоточенной вся масса системы.

Дифференцируя (26) еще раз по времени и вспоминая тео­рему количества движения (24), будем иметь

(27)

Отсюда вытекает теорема о движении центра масс: центр масс системы движется как точка, в которой сосредо­точена вся масса системы и к которой приложен главный вектор внешних сил, действующих на систему.

Из приведенной формулировки следует, что внутренние силы не влияют на движение центра масс; только внешние силы мо­гут изменять его движение. Если система находится в покое, то внутренними силами нельзя вывести из покоя ее центр масс; вызванное внутренними силами движение системы будет про­исходить так, что центр масс останется неподвижным. Точно так же, если центр масс находился в движении, то внутренними силами нельзя изменить его движение.

Остановимся на некоторых частных случаях движения си­стемы.

1. Главный вектор внешних сил равен нулю. В этом случае из уравнения (27) следует, что центр масс находится в покое или движется прямолинейно и равномерно. Будет ли иметь место покой или движение, за­висит от начальных условий. Пусть система находилась в покое. Дважды интегрируя уравнение (23) имеем

или, введя получим Необходимо помнить, что во всех общих теоремах динамики перемещения, скорости и ускорения должны рассматриваться в неподвижной системе отсчёта, т.е. абсолютными.

2. Рассмотрим движение автомобиля по горизонтальному пути; внутренние силы не могут привести его в движение, так как только внешние силы создают изменение движения центра масс. Этими внешними силами являются: сила тяжести, ре­акции дороги и сопротивление воздуха . Единственной движущей силой является горизонтальная составляющая реакции дороги, т. е. сила трения скольжения меж­ду ведущими колесами и дорогой!! Ведомые колеса, наоборот, лишь тормозят движение. Рассмотрим простейшую модель разгона автомобиля. Возьмём переднеприводную машину, на передние колёса которой приходится 0.6 массы автомобиля, тогда имеем

Зададимся вопросом: каким должен быть коэффициент трения f , чтобы разогнать автомобиль до 100 км/час за 5 секунд? Считая силу трения постоянной и движение равноускоренным, получим , а после подстановки чисел f = .Обычно коэффициент силы трения колеса и шоссе принимают равной в пределах. В рассматриваемой модели не учитывается сопротивление воздуха, торможение ведомых колёс и трение качения. Учёт этих сил увеличивает необходимый для разгона коэффициент трения.