- •1.Марковский процесс с дискретными состояниями и дискретным временем.
- •2.Циклический процесс
- •3.Процесс “Гибели и размножения”
- •4. Смо типа m/m/m
- •6. Многоканальная смо с ограниченным ожиданием m/m/m/k
- •7. Замкнутая многоканальная смо (m/m/m/k/l)
- •8. Распределение числа требований в системе m/g/1/
- •9. Распределение времени пребывания в системе m/g/1
- •10.Уравнение Поллячика–Хинчина для преобразования Лапласа в системе m/g/1
- •11. Формула Поллячика - Хинчина для среднего значения в системе m/g/1
- •12. Теорема Бёрка (Burke)
- •13. Разложение времени сетевой задержки по каналам сети
- •14. Задача выбора пропускных способностей каналов
- •15. Смо типа m/m/1
- •16. Одноканальная смо с отказами (m/m/1/0)
- •17. Одноканальная смо с ограниченным ожиданием (m/m/1/k).
- •18. Одноканальные замкнутые смо (m/m/1/k/l).
- •19.Многоканальная смо с отказами (m/m/m/0)
17. Одноканальная смо с ограниченным ожиданием (m/m/1/k).
В этой модели количество мест в очереди равно k, что и накладывает ограничение на время ожидания каждого требования, т. е. (W<k/). Время ожидания не превышает k обсл.
Будем нумеровать состояния СМО по числу требований, находящихся в системе.
S0 – канал свободен
S1 – канал занят, очереди нет
…
Sk+1 – канал занят, в очереди k заявок

Пользуясь общим решением схемы «гибели и размножения» и введя обозначение =/, получим:
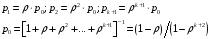
Выражение для p0 справедливо для <1, при:

Заявка получает отказ, когда все k мест в очереди заняты:
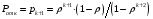
Оставшаяся доля заявок будет обслужена, поэтому относительная пропускная способность:
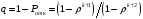
Абсолютная
пропускная способность: A= q.
q.
Выводы
выражения для среднего времени ожидания
пребывания в очереди (W).
Любая заявка с вероятностью p0
не будет ждать обслуживания (время
ожидания=0), с вероятностью p1
будет ждать одного обслуживания (время
ожидания=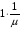 ),
с вероятностью p2
будет ждать одного обслуживания (время
ожидания=
),
с вероятностью p2
будет ждать одного обслуживания (время
ожидания=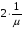 )
и т. д.
)
и т. д.
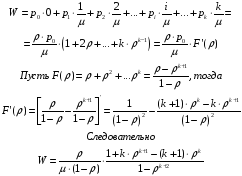
Время обслуживания X равно 1/, если заявка обслуживается и X=0, если она получила отказ.

18. Одноканальные замкнутые смо (m/m/1/k/l).
Одноканальные замкнутые СМО (M/M/1/k/l).
Характерным для замкнутой системы массового обслуживания является наличие ограниченного числа источником заявок и, следовательно, интенсивность входного потока зависит от состояния самой системы.
В сущности, любая СМО имеет дело только с ограниченным числом источников заявок, но в ряде случаев число этих источников так велико, что можно пренебречь влиянием состояния СМО на поток заявок (АТС крупного города).
В замкнутой СМО источники заявок, наряду с каналами обслуживания, рассматриваются как элементы СМО.
Пусть m – число каналов обслуживания, l – число источников заявок, k – число мест в очереди (kl-1), - интенсивность обслуживания.
S0 – канал свободен
S1 – канал занят, очереди нет
Sl – канал занят, в очереди l-1 требований
Из
состояния S0
в
состояние S1
систему
переводит поток l,
из S1
в S2
уже (l
-1) ,
т. к. один источник заявок не функционирует
и ожидает обслуживания. Из S2
в S3
в имеем поток (l
-2)
,
т. к. один источник заявок не функционирует
и ожидает обслуживания. Из S2
в S3
в имеем поток (l
-2)
и т. д.
и т. д.
kl-1
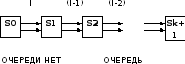
Пользуясь общим решением для схемы гибели и размножения, напишем:
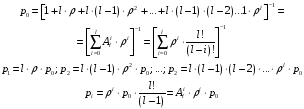
Относительная пропускная способность q=1, Pотн=0 т. к. каждое требование будет, в конце концов, обслужено.
Pзан=(1–p0) – вероятность, что канал занят. Занятый канал обслуживает в среднем требований в единицу времени, следовательно, абсолютная пропускная способность:
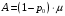
В СМО в среднем работает (l-N) источников заявок, каждый из которых поток интенсивность которого =.
Общий
поток требований (l-N)
будет обслужен и, следовательно, равен
абсолютной пропускной способности:
будет обслужен и, следовательно, равен
абсолютной пропускной способности:
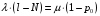
Откуда среднее число требований, находящихся в СМО:
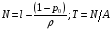
Значение N можно вычислить непосредственно:
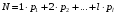
Среднее число требований, находящихся в обслуживающем устройстве равно:
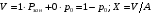
Среднее число требований, ожидающих обсл. в очереди:

Эта система является саморегулируемой. Когда она перегружается, т. е. Образуется большая очередь, то интенсивность поступления дополнительных требований убывает.
Если kl-1

Пример. Система коллективного доступа реализует вычислительный процесс, обрабатывая запросы трех других периферийных систем обработки информации.
Определить эксплуатационные характеристики системы.
Решение.
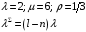


Вероятность занятости системы коллективного доступа:
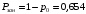
Абсолютная пропускная способность системы:
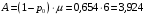
Среднее число запросов в системе:
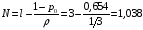
Среднее число требований в обслуживающем устройстве:
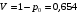
Среднее число требований в ожидающем устройстве: