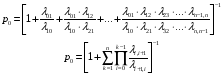1.Марковский процесс с дискретными состояниями и дискретным временем.

Марковский процесс с дискретными состояниями и непрерывным временем ещё называют непрерывной цепью Маркова.

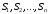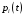Пусть имеется ряд дискретных состояний . Обозначим через вероятность того, что в момент времени 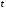система 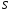будет находиться в состоянии 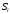, где .

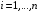Определим для любого момента времени 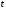вероятности состояний:

и рассмотрим элементарный промежуток времени 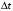, примыкающий справа к моменту времени .

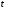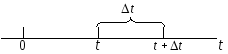
Назовем плотностью вероятности перехода 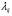– предел отношения вероятности 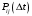– перехода системы за время 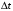из состояния 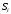в состояние 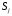к длине промежутка

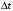
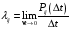
Если все плотности вероятностей перехода 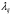не зависят от 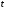, то непрерывную цепь Маркова называют однородной; если эти плотности представляют функции времени, то процесс называется неоднородным.

Пометим каждую стрелку графа состояний соответствующей плотностью вероятностей перехода. Такой граф называют размеченным графом состояний.

Покажем, что, зная размеченный граф состояний, можно определить вероятность состояний 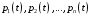как решение дифференциальных уравнений Колмогорова.

Пример:

Система 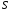имеет четыре возможных состояния .

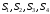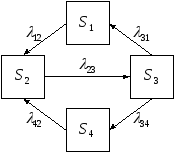
Найдем вероятность .

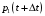Это событие может произойти двумя способами:

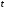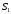1. В момент времени система была в состоянии , а за время 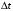ничего не изменилось:

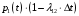
2. В момент времени 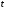система была в состоянии 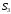, а за время 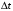перешла в состояние :

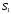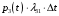
Применяя правило сложения вероятностей, получим:

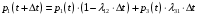
или

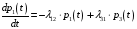
Таким образом, выведено дифференциальное уравнение, которому должна удовлетворять функция .

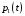Рассуждая аналогично, получим систему дифференциальных уравнений Колмогорова:

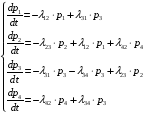
Заметим, что всегда справедливо: .

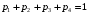Таким образом, при в системе 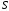устанавливается некоторый стационарный режим: он состоит в том, что система случайным образом меняет свои состояния, но вероятность каждого из них уже не зависит от времени: каждое из состояний осуществляется с некоторой постоянной вероятностью, которая представляет собой среднее относительное время пребывания системы в данном состоянии. Для вычисления финальных вероятностей достаточно в системе уравнений Колмогорова все левые части положить равными нулю.

2.Циклический процесс

Марковский случайный процесс, протекающий в системе, называется циклическим, если состояния связаны между собой в кольцо с односторонними переходами.

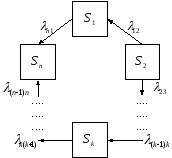
Алгебраические уравнения для предельных вероятностей состояний имеют следующий вид:

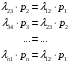
Решая эти уравнения, получим:

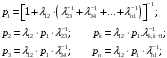
После элементарных преобразований получим

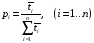
то есть финальные вероятности состояний в циклической схеме относятся как средние времена пребывания системы в каждом из состояний.

3.Процесс “Гибели и размножения”

Марковская непрерывная цепь называется процессом «гибели и размножения», если её граф состояний имеет следующий вид:

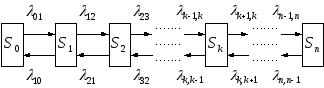
Происхождение термина «схема гибели и размножения» ведёт начало от биологических задач, где подобной схемой описывается процесс изменения численности популяции.

Рассмотрим случайный процесс «гибели и размножения». Для него справедлива следующая система алгебраических уравнений:

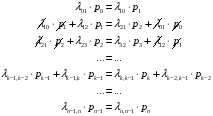
и нормированное уравнение .

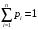Решая эту систему, получим:

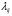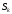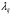В числителе стоит произведение всех плотностей вероятности перехода (интенсивности) , стоящих у стрелок, направленных слева направо с начала и вплоть до той, которая идет в состояние ; в знаменателе стоит произведение всех интенсивностей , стоящих у стрелок, идущих справа налево с начала и вплоть до стрелки, исходящей из состояния .

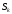Из нормировочного условия получим: