- •Оглавление
- •Часть 1 4
- •Элементы линейной алгебры
- •1.2. Матрицы и операции над ними
- •1.3. Вычисление обратной матрицы
- •1.4. Решение матричных уравнений
- •1.5. Вычисление ранга матрицы
- •1.6. Правило Крамера
- •1.7. Метод полного исключения неизвестных Жордана-Гаусса
- •1.8. Однородные системы линейных уравнений
- •1.9. Действия над векторами
- •1.10. Линейная зависимость и независимость векторов
- •1.11. Базис системы векторов. Переход от одного базиса к другому
- •1.12. Квадратичные формы
- •1.13. Линейные операторы
1.11. Базис системы векторов. Переход от одного базиса к другому
Базисом системы векторов называется такая ее подсистема, которая:
1) является линейно-независимой;
2) любой вектор из системы векторов можно выразить как линейную комбинацию этой подсистемы векторов.
Базис в n-мерном пространстве содержит n линейно-независимых векторов. В пространстве (мы рассматриваем арифметические пространства) существует бесчисленное множество базисов. Одним из базисов пространства является система единичных векторов ei (i=l,2,...,n), у которых все компоненты, кроме i-той, равны нулю, а i-я компонента равна единице. Любой вектор пространства можно представить как линейную комбинацию векторов базиса. Например, если кроме системы единичных векторов:
 =(1,0,0,…,0),
=(1,0,0,…,0),
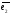 =(0,1,0,…,0),
=(0,1,0,…,0),
……………….
 =(0,0,0,…,1),
=(0,0,0,…,1),
задан вектор
 ,
то данный вектор можно представить в
виде:
,
то данный вектор можно представить в
виде:
 .
.
Коэффициентами
разложения данного вектора по векторам
базиса являются его координаты. В каждом
базисе вектору
 соответствует строка его координат.
Это разложение вектора
соответствует строка его координат.
Это разложение вектора
 по данному базису является единственным.
Например, если дан базис в n-мерном
пространстве в виде системы векторов
по данному базису является единственным.
Например, если дан базис в n-мерном
пространстве в виде системы векторов
 ,
,
отличный от базиса единичных векторов, то разложение вектора в данном базисе будет иным:
 ,
,
где
 -
координаты вектора
-
координаты вектора
 в новом базисе.
в новом базисе.
Рассмотрим задачу перехода от одного базиса к другому. Пусть в n-мерном пространстве дан базис в виде системы единичных векторов и новый базис в виде системы векторов:
 ,
где (i=l, 2,..., n).
,
где (i=l, 2,..., n).
Задан также вектор
 в старом базисе, т.е. в базисе из единичных
векторов. Требуется перейти из старого
базиса к новому, т.е. найти координаты
единичных векторов, а также координаты
вектора
в старом базисе, т.е. в базисе из единичных
векторов. Требуется перейти из старого
базиса к новому, т.е. найти координаты
единичных векторов, а также координаты
вектора
 в новом базисе.
в новом базисе.
Этот переход можно
осуществить при помощи метода
Жордана-Гаусса. Для этого надо составить
матрицу, в которой записать сначала
векторы старого базиса, затем нового
базиса и, наконец, вектор
 .
Координаты каждого вектора будут
записаны в столбце. В результате получим
матрицу:
.
Координаты каждого вектора будут
записаны в столбце. В результате получим
матрицу:

Умножая каждую
часть матрицы на обратную матрицу
 слева,
будем иметь:
слева,
будем иметь:

т.е.
в первой части получим в каждом столбце
координаты соответствующего вектора
старого базиса в новом базисе, во второй
- новый базис в виде единичных векторов,
в третьей - координаты вектора
 в новом базисе.
в новом базисе.
Таким образом,
наша задача сводится к тому, чтобы путем
преобразований методом Жордана-Гаусса
получить во второй части единичную
матрицу. Если это нельзя сделать, то
система векторов
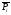 (1=1,2,...,n) является
линейно-зависимой и, следовательно, не
образует базис.
(1=1,2,...,n) является
линейно-зависимой и, следовательно, не
образует базис.
Пример. Даны
базисы в виде системы векторов
 =(1,
0, 0),
=(1,
0, 0),
 =(0,1,
0),
=(0,1,
0),
 =(0,
0,1) и системы векторов
=(0,
0,1) и системы векторов
![]() =(2,
4, 0),
=(2,
4, 0),
 =(3,1,2)
и
=(3,1,2)
и
 =(1,
2, -1). Выразить векторы
=(1,
2, -1). Выразить векторы
 ,
, ,
, через векторы
через векторы
 ,
, ,
,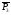 .
Найти во втором базисе координаты
вектора
.
Найти во втором базисе координаты
вектора
 =(0,
-5, 5), заданного в первом базисе. Выразим
векторы
=(0,
-5, 5), заданного в первом базисе. Выразим
векторы
 через
через
 :
:

Таблица 1.11.1.
|
Базис
|
|
|
|
|
|
|
X
|
примечание
|
|
|
1
|
0
|
0
|
2
|
3
|
1
|
0
|
1 строка
|
|
|
0
|
1
|
0
|
4
|
1
|
2
|
-5
|
2 строка
|
|
|
0
|
0
|
1
|
0
|
2
|
-1
|
5
|
3 строка
|
|
|
1/2
|
0
|
0
|
1
|
3/2
|
1/2
|
0
|
4 стр.=1стр./2
|
|
|
|
|
|
|
|
|
|
|
|
|
-2
|
1
|
0
|
0
|
-5
|
0
|
-5
|
5 стр.=2стр.+ 4стр. • (- 4)
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
0
|
1
|
0
|
2
|
-1
|
5
|
6 стр.=3стр.
|
|
|
-1/10
|
3/10
|
0
|
1
|
0
|
1/2
|
-3/2
|
7 стр.=4стр.+8стр.* (-3/2)
|
|
|
|
|
|
|
|
|
|
|
|
|
2/5
|
-1/5
|
0
|
0
|
1
|
0
|
1
|
8 стр.=5стр./(-5)
|
|
|
|
|
|
|
|
|
|
|
|
|
-4/5 |
2/5
|
1
|
0
|
0
|
-1
|
3
|
9 стр.=6 стр.+8 стр.*(-2)
|
|
|
|
|
|
|
|
|
|
|
|
|
-1/2
|
1/2
|
1/2
|
1
|
0
|
0
|
0
|
10 стр,=7стр.+ 12стр. • (-1/2)
|
|
|
|
|
|
|
|
|
|
|
|
|
2/5
|
-1/5
|
0
|
0
|
1
|
0
|
1
|
11 стр.-8 стр.
|
|
|
|
|
|
|
|
|
|
|
|
|
4/5 |
-2/5
|
.-1
|
0
|
0
|
1
|
-3
|
12 стр.=9стр.:/(-1)
|
|
|
|
|
|
|
|
|
|
|
Решение. Все
вычисления будем производить в таблице
1.11.1., в столбцах которой запишем координаты
данных векторов в базисе
 ,
, ,
, .
.
В таблице слева
оставим одну графу для записи базисных
векторов. Каждым шагом метода Жордана-Гаусса
заменяем один базисный вектор другим.
Все произведенные действия над строками
указаны в примечаниях таблицы. Отметим,
что необязательно первый шаг начинать
с введения в базис вектора
 .
Удобнее ввести в базис сначала вектор
.
Удобнее ввести в базис сначала вектор
 ,
так как он имеет в первой строке «1». В
последнем шаге записаны конечные
результаты. Так, вектор
,
так как он имеет в первой строке «1». В
последнем шаге записаны конечные
результаты. Так, вектор
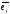 в новом базисе имеет координаты
в новом базисе имеет координаты
 ;
т.е.
;
т.е.

Аналогично запишем и разложения других единичных векторов по векторам нового базиса:
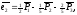

Вектор
 в новом базисе имеет координаты (0, 1,
-3).
в новом базисе имеет координаты (0, 1,
-3).
Упражнения.
1.11.1. Написать
разложение вектора
 =(3,
4, -2) в базисе
=(3,
4, -2) в базисе
 =(1,
0, 0),
=(1,
0, 0),
 =(0,1,
0),
=(0,1,
0),
 =(0,
0,1).
=(0,
0,1).
1.11.2. Показать, что
векторы
 =(1,
2) и
=(1,
2) и
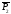 =(0,
3) образуют базис. Найти координаты
вектора
=(0,
3) образуют базис. Найти координаты
вектора
 =(3, 0) в этом базисе. Результаты проверить
графически.
=(3, 0) в этом базисе. Результаты проверить
графически.
1.11.3. Векторы
 =(1,
1, 1),
=(1,
1, 1),
 =(1,1,2),
=(1,1,2),
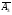 =(1,2,3)
и
=(1,2,3)
и
 =(6,
9, 14) заданы в некотором базисе. Показать,
что векторы
=(6,
9, 14) заданы в некотором базисе. Показать,
что векторы
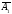 ,
, ,
,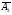 -
образуют базис. Найти координаты вектора
-
образуют базис. Найти координаты вектора
 в этом базисе.
в этом базисе.
1.11.4. Показать, что
векторы
 =(2,
1, -3),
=(2,
1, -3),
 =(3,
2, -5),
=(3,
2, -5),
 =(1,
-1, 1)
=(1,
-1, 1)
образуют базис.
Найти координаты вектора =(6, 2,- 7) в этом базисе.
=(6, 2,- 7) в этом базисе.
1.11.5. Показать, что
векторы
 =(1,0,3),
=(1,0,3),
 =(-2,1,1) и
=(-2,1,1) и
 =(0,2,4)
образуют базис. Найти координаты вектора
=(0,2,4)
образуют базис. Найти координаты вектора
 =(-9,6, 11) в этом базисе.
=(-9,6, 11) в этом базисе.
1.11.6. Показать, что
векторы
 =(1,2,-
1,2),
=(1,2,-
1,2),
 =
(2,3,0,- 1),
=
(2,3,0,- 1),
 =
(1,2,1,3) и
=
(1,2,1,3) и
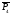 =(1,3,-
1,1) образуют базис. Найти координаты
вектора
=(1,3,-
1,1) образуют базис. Найти координаты
вектора
 =(7,14,-
1,1) в этом базисе.
=(7,14,-
1,1) в этом базисе.
Доказать, что каждая из двух систем векторов является базисом. Найти связь между координатами векторов обоих базисов.
1.11.7.
 =(1,0),
=(1,0),
 =(0,1),
=(0,1),
 =(2,3)
и
=(2,3)
и
 =(1,2);
=(1,2);
1.11.8.
 =(1,0,0),
=(1,0,0),
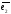 =(0,1,0),
=(0,1,0),
 =(0,0,1),
=(0,0,1),
 =(-1,0,2),
=(-1,0,2),
 =(2,1,0) и
=(2,1,0) и
 =(4,2,1);
=(4,2,1);
1.11.9.
 =(4,2,1),
=(4,2,1),
 =(2,0,3),
=(2,0,3),
 =(0,7,1),
=(0,7,1),
 =(3,1,9),
=(3,1,9),
 =(0,2,1)
и
=(0,2,1)
и
 =(-1,1,-
6);
=(-1,1,-
6);
1.11.10.
 =
(1,1,1,1),
=
(1,1,1,1),
 =(1,2,1,1),г,
=(1,2,1,1),г,
 =
(1,1,2,1),
=
(1,1,2,1),
 =(1,3,2,3),
=(1,3,2,3),
 =(1;0,3,3),
=(1;0,3,3),
 =
=
=(-2,-3,-5,-4),
 =(2,2,5,4)
и
=(2,2,5,4)
и
 =
(-2,-3,-4,-4);
=
(-2,-3,-4,-4);
1.11.11.Даны векторы
 =(1,3),
=(1,3),
 (2,4),
(2,4),
 =(4,3)
в базисе
=(4,3)
в базисе
 =(1,0),
=(1,0),
 =(0,1).
Показать, что векторы
=(0,1).
Показать, что векторы
 и
и
 образуют базис. Найти связь между
векторами нового и старого базисов.
Найти координаты вектора
образуют базис. Найти связь между
векторами нового и старого базисов.
Найти координаты вектора
 в новом базисе.
в новом базисе.
1.11.12.Даны векторы:
 =(1,1,1),
=(1,1,1),
 =(1,2,1),
=(1,2,1),
 =(3,2,1)
- базис и
=(3,2,1)
- базис и
 =(0,2,2)
в базисе
=(0,2,2)
в базисе
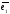 =(1,0,0),
=(1,0,0),
 =(0,1,0),
=(0,1,0),
 =(0,0,1).
Найти связь между новым и старым базисом.
Найти координаты вектора
=(0,0,1).
Найти связь между новым и старым базисом.
Найти координаты вектора
 в новом базисе.
в новом базисе.
1.11.13. Даны векторы
 =(1,1,1),
=(1,1,1),
 =(1,1,2),
=(1,1,2),
 =(1,2,3),
=(1,2,3),
 =(-6,3,1),
=(-6,3,1),
 =(1,-
1,0),
=(1,-
1,0),
 =(2,1,3),
=(2,1,3),
 =(1,2,-
1). Показать, что векторы
=(1,2,-
1). Показать, что векторы
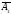 ,
, ,
, образуют
базис. Выразить в этом базисе все
остальные векторы.
образуют
базис. Выразить в этом базисе все
остальные векторы.